More on Web3 & Crypto

William Brucee
3 years ago
This person is probably Satoshi Nakamoto.

Who founded bitcoin is the biggest mystery in technology today, not how it works.
On October 31, 2008, Satoshi Nakamoto posted a whitepaper to a cryptography email list. Still confused by the mastermind who changed monetary history.
Journalists and bloggers have tried in vain to uncover bitcoin's creator. Some candidates self-nominated. We're still looking for the mystery's perpetrator because none of them have provided proof.
One person. I'm confident he invented bitcoin. Let's assess Satoshi Nakamoto before I reveal my pick. Or what he wants us to know.
Satoshi's P2P Foundation biography says he was born in 1975. He doesn't sound or look Japanese. First, he wrote the whitepaper and subsequent articles in flawless English. His sleeping habits are unusual for a Japanese person.
Stefan Thomas, a Bitcoin Forum member, displayed Satoshi's posting timestamps. Satoshi Nakamoto didn't publish between 2 and 8 p.m., Japanese time. Satoshi's identity may not be real.
Why would he disguise himself?
There is a legitimate explanation for this
Phil Zimmermann created PGP to give dissidents an open channel of communication, like Pretty Good Privacy. US government seized this technology after realizing its potential. Police investigate PGP and Zimmermann.
This technology let only two people speak privately. Bitcoin technology makes it possible to send money for free without a bank or other intermediary, removing it from government control.
How much do we know about the person who invented bitcoin?
Here's what we know about Satoshi Nakamoto now that I've covered my doubts about his personality.
Satoshi Nakamoto first appeared with a whitepaper on metzdowd.com. On Halloween 2008, he presented a nine-page paper on a new peer-to-peer electronic monetary system.

Using the nickname satoshi, he created the bitcointalk forum. He kept developing bitcoin and created bitcoin.org. Satoshi mined the genesis block on January 3, 2009.
Satoshi Nakamoto worked with programmers in 2010 to change bitcoin's protocol. He engaged with the bitcoin community. Then he gave Gavin Andresen the keys and codes and transferred community domains. By 2010, he'd abandoned the project.
The bitcoin creator posted his goodbye on April 23, 2011. Mike Hearn asked Satoshi if he planned to rejoin the group.
“I’ve moved on to other things. It’s in good hands with Gavin and everyone.”
Nakamoto Satoshi
The man who broke the banking system vanished. Why?

Satoshi's wallets held 1,000,000 BTC. In December 2017, when the price peaked, he had over US$19 billion. Nakamoto had the 44th-highest net worth then. He's never cashed a bitcoin.
This data suggests something happened to bitcoin's creator. I think Hal Finney is Satoshi Nakamoto .
Hal Finney had ALS and died in 2014. I suppose he created the future of money, then he died, leaving us with only rumors about his identity.
Hal Finney, who was he?
Hal Finney graduated from Caltech in 1979. Student peers voted him the smartest. He took a doctoral-level gravitational field theory course as a freshman. Finney's intelligence meets the first requirement for becoming Satoshi Nakamoto.
Students remember Finney holding an Ayn Rand book. If he'd read this, he may have developed libertarian views.
His beliefs led him to a small group of freethinking programmers. In the 1990s, he joined Cypherpunks. This action promoted the use of strong cryptography and privacy-enhancing technologies for social and political change. Finney helped them achieve a crypto-anarchist perspective as self-proclaimed privacy defenders.
Zimmermann knew Finney well.
Hal replied to a Cypherpunk message about Phil Zimmermann and PGP. He contacted Phil and became PGP Corporation's first member, retiring in 2011. Satoshi Nakamoto quit bitcoin in 2011.
Finney improved the new PGP protocol, but he had to do so secretly. He knew about Phil's PGP issues. I understand why he wanted to hide his identity while creating bitcoin.
Why did he pretend to be from Japan?
His envisioned persona was spot-on. He resided near scientist Dorian Prentice Satoshi Nakamoto. Finney could've assumed Nakamoto's identity to hide his. Temple City has 36,000 people, so what are the chances they both lived there? A cryptographic genius with the same name as Bitcoin's creator: coincidence?
Things went differently, I think.
I think Hal Finney sent himself Satoshis messages. I know it's odd. If you want to conceal your involvement, do as follows. He faked messages and transferred the first bitcoins to himself to test the transaction mechanism, so he never returned their money.
Hal Finney created the first reusable proof-of-work system. The bitcoin protocol. In the 1990s, Finney was intrigued by digital money. He invented CRypto cASH in 1993.
Legacy
Hal Finney's contributions should not be forgotten. Even if I'm wrong and he's not Satoshi Nakamoto, we shouldn't forget his bitcoin contribution. He helped us achieve a better future.

Nabil Alouani
3 years ago
Why Cryptocurrency Is Not Dead Despite the FTX Scam
A fraud, free-market, antifragility tale

Crypto's only rival is public opinion.
In less than a week, mainstream media, bloggers, and TikTokers turned on FTX's founder.
While some were surprised, almost everyone with a keyboard and a Twitter account predicted the FTX collapse. These financial oracles should have warned the 1.2 million people Sam Bankman-Fried duped.
After happening, unexpected events seem obvious to our brains. It's a bug and a feature because it helps us cope with disasters and makes our reasoning suck.
Nobody predicted the FTX debacle. Bloomberg? Politicians. Non-famous. No cryptologists. Who?
When FTX imploded, taking billions of dollars with it, an outrage bomb went off, and the resulting shockwave threatens the crypto market's existence.
As someone who lost more than $78,000 in a crypto scam in 2020, I can only understand people’s reactions. When the dust settles and rationality returns, we'll realize this is a natural occurrence in every free market.
What specifically occurred with FTX? (Skip if you are aware.)
FTX is a cryptocurrency exchange where customers can trade with cash. It reached #3 in less than two years as the fastest-growing platform of its kind.
FTX's performance helped make SBF the crypto poster boy. Other reasons include his altruistic public image, his support for the Democrats, and his company Alameda Research.
Alameda Research made a fortune arbitraging Bitcoin.
Arbitrage trading uses small price differences between two markets to make money. Bitcoin costs $20k in Japan and $21k in the US. Alameda Research did that for months, making $1 million per day.
Later, as its capital grew, Alameda expanded its trading activities and began investing in other companies.
Let's now discuss FTX.
SBF's diabolic master plan began when he used FTX-created FTT coins to inflate his trading company's balance sheets. He used inflated Alameda numbers to secure bank loans.
SBF used money he printed himself as collateral to borrow billions for capital. Coindesk exposed him in a report.
One of FTX's early investors tweeted that he planned to sell his FTT coins over the next few months. This would be a minor event if the investor wasn't Binance CEO Changpeng Zhao (CZ).
The crypto space saw a red WARNING sign when CZ cut ties with FTX. Everyone with an FTX account and a brain withdrew money. Two events followed. FTT fell from $20 to $4 in less than 72 hours, and FTX couldn't meet withdrawal requests, spreading panic.
SBF reassured FTX users on Twitter. Good assets.
He lied.
SBF falsely claimed FTX had a liquidity crunch. At the time of his initial claims, FTX owed about $8 billion to its customers. Liquidity shortages are usually minor. To get cash, sell assets. In the case of FTX, the main asset was printed FTT coins.
Sam wouldn't get out of trouble even if he slashed the discount (from $20 to $4) and sold every FTT. He'd flood the crypto market with his homemade coins, causing the price to crash.
SBF was trapped. He approached Binance about a buyout, which seemed good until Binance looked at FTX's books.
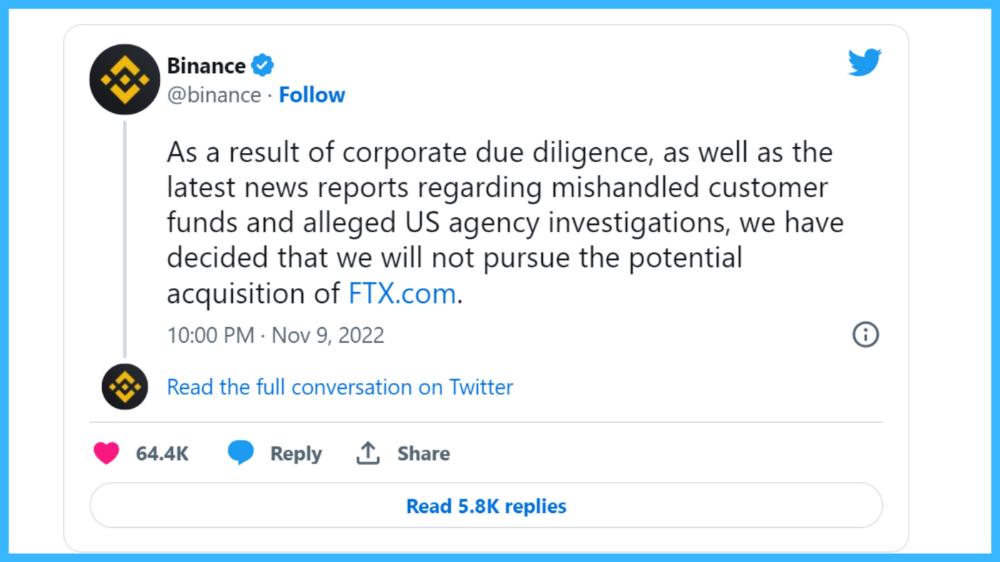
Binance's tweet ended SBF, and he had to apologize, resign as CEO, and file for bankruptcy.
Bloomberg estimated Sam's net worth to be zero by the end of that week. 0!
But that's not all. Twitter investigations exposed fraud at FTX and Alameda Research. SBF used customer funds to trade and invest in other companies.
Thanks to the Twitter indie reporters who made the mainstream press look amateurish. Some Twitter detectives didn't sleep for 30 hours to find answers. Others added to existing threads. Memes were hilarious.
One question kept repeating in my bald head as I watched the Blue Bird. Sam, WTF?
Then I understood.
SBF wanted that FTX becomes a bank.
Think about this. FTX seems healthy a few weeks ago. You buy 2 bitcoins using FTX. You'd expect the platform to take your dollars and debit your wallet, right?
No. They give I-Owe-Yous.
FTX records owing you 2 bitcoins in its internal ledger but doesn't credit your account. Given SBF's tricks, I'd bet on nothing.
What happens if they don't credit my account with 2 bitcoins? Your money goes into FTX's capital, where SBF and his friends invest in marketing, political endorsements, and buying other companies.
Over its two-year existence, FTX invested in 130 companies. Once they make a profit on their purchases, they'll pay you and keep the rest.
One detail makes their strategy dumb. If all FTX customers withdraw at once, everything collapses.
Financially savvy people think FTX's collapse resembles a bank run, and they're right. SBF designed FTX to operate like a bank.
You expect your bank to open a drawer with your name and put $1,000 in it when you deposit $1,000. They deposit $100 in your drawer and create an I-Owe-You for $900. What happens to $900?
Let's sum it up: It's boring and headache-inducing.
When you deposit money in a bank, they can keep 10% and lend the rest. Fractional Reserve Banking is a popular method. Fractional reserves operate within and across banks.
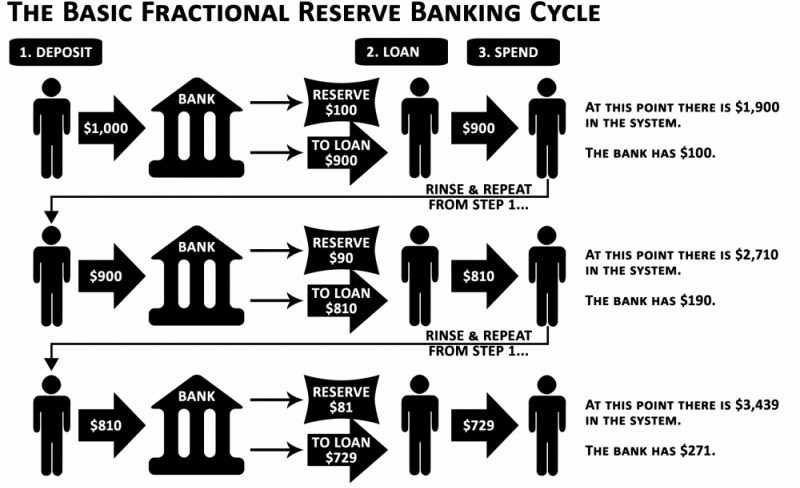
Fractional reserve banking generates $10,000 for every $1,000 deposited. People will pay off their debt plus interest.
As long as banks work together and the economy grows, their model works well.
SBF tried to replicate the system but forgot two details. First, traditional banks need verifiable collateral like real estate, jewelry, art, stocks, and bonds, not digital coupons. Traditional banks developed a liquidity buffer. The Federal Reserve (or Central Bank) injects massive cash into troubled banks.
Massive cash injections come from taxpayers. You and I pay for bankers' mistakes and annual bonuses. Yes, you may think banking is rigged. It's rigged, but it's the best financial game in 150 years. We accept its flaws, including bailouts for too-big-to-fail companies.
Anyway.
SBF wanted Binance's bailout. Binance said no, which was good for the crypto market.
Free markets are resilient.
Nassim Nicholas Taleb coined the term antifragility.
“Some things benefit from shocks; they thrive and grow when exposed to volatility, randomness, disorder, and stressors and love adventure, risk, and uncertainty. Yet, in spite of the ubiquity of the phenomenon, there is no word for the exact opposite of fragile. Let us call it antifragile. Antifragility is beyond resilience or robustness. The resilient resists shocks and stays the same; the antifragile gets better.”
The easiest way to understand how antifragile systems behave is to compare them with other types of systems.
Glass is like a fragile system. It snaps when shocked.
Similar to rubber, a resilient system. After a stressful episode, it bounces back.
A system that is antifragile is similar to a muscle. As it is torn in the gym, it gets stronger.
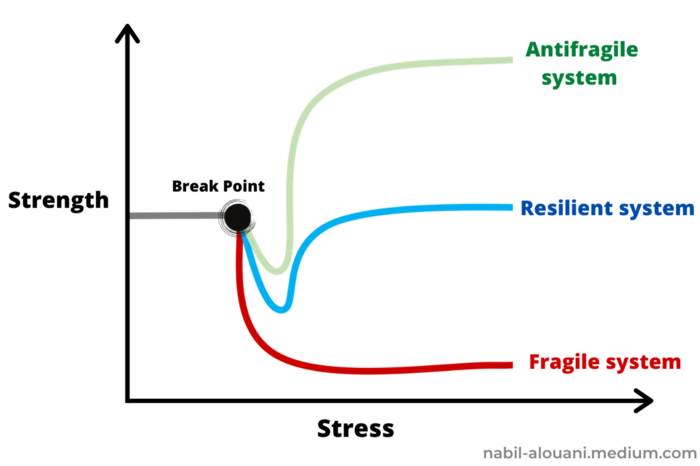
Time-changed things are antifragile. Culture, tech innovation, restaurants, revolutions, book sales, cuisine, economic success, and even muscle shape. These systems benefit from shocks and randomness in different ways, but they all pay a price for antifragility.
Same goes for the free market and financial institutions. Taleb's book uses restaurants as an example and ends with a reference to the 2008 crash.
“Restaurants are fragile. They compete with each other. But the collective of local restaurants is antifragile for that very reason. Had restaurants been individually robust, hence immortal, the overall business would be either stagnant or weak and would deliver nothing better than cafeteria food — and I mean Soviet-style cafeteria food. Further, it [the overall business] would be marred with systemic shortages, with once in a while a complete crisis and government bailout.”
Imagine the same thing with banks.
Independent banks would compete to offer the best services. If one of these banks fails, it will disappear. Customers and investors will suffer, but the market will recover from the dead banks' mistakes.
This idea underpins a free market. Bitcoin and other cryptocurrencies say this when criticizing traditional banking.
The traditional banking system's components never die. When a bank fails, the Federal Reserve steps in with a big taxpayer-funded check. This hinders bank evolution. If you don't let banking cells die and be replaced, your financial system won't be antifragile.
The interdependence of banks (centralization) means that one bank's mistake can sink the entire fleet, which brings us to SBF's ultimate travesty with FTX.
FTX has left the cryptocurrency gene pool.
FTX should be decentralized and independent. The super-star scammer invested in more than 130 crypto companies and linked them, creating a fragile banking-like structure. FTX seemed to say, "We exist because centralized banks are bad." But we'll be good, unlike the centralized banking system.
FTX saved several companies, including BlockFi and Voyager Digital.
FTX wanted to be a crypto bank conglomerate and Federal Reserve. SBF wanted to monopolize crypto markets. FTX wanted to be in bed with as many powerful people as possible, so SBF seduced politicians and celebrities.
Worst? People who saw SBF's plan flaws praised him. Experts, newspapers, and crypto fans praised FTX. When billions pour in, it's hard to realize FTX was acting against its nature.
Then, they act shocked when they realize FTX's fall triggered a domino effect. Some say the damage could wipe out the crypto market, but that's wrong.
Cell death is different from body death.
FTX is out of the game despite its size. Unfit, it fell victim to market natural selection.
Next?
The challengers keep coming. The crypto economy will improve with each failure.
Free markets are antifragile because their fragile parts compete, fostering evolution. With constructive feedback, evolution benefits customers and investors.
FTX shows that customers don't like being scammed, so the crypto market's health depends on them. Charlatans and con artists are eliminated quickly or slowly.
Crypto isn't immune to collapse. Cryptocurrencies can go extinct like biological species. Antifragility isn't immortality. A few more decades of evolution may be enough for humans to figure out how to best handle money, whether it's bitcoin, traditional banking, gold, or something else.
Keep your BS detector on. Start by being skeptical of this article's finance-related claims. Even if you think you understand finance, join the conversation.
We build a better future through dialogue. So listen, ask, and share. When you think you can't find common ground with the opposing view, remember:
Sam Bankman-Fried lied.

Jayden Levitt
3 years ago
The country of El Salvador's Bitcoin-obsessed president lost $61.6 million.
It’s only a loss if you sell, right?

Nayib Bukele proclaimed himself “the world’s coolest dictator”.
His jokes aren't clear.
El Salvador's 43rd president self-proclaimed “CEO of El Salvador” couldn't be less presidential.
His thin jeans, aviator sunglasses, and baseball caps like a cartel lord.
He's popular, though.
Bukele won 53% of the vote by fighting violent crime and opposition party corruption.
El Salvador's 6.4 million inhabitants are riding the cryptocurrency volatility wave.
They were powerless.
Their autocratic leader, a former Yamaha Motors salesperson and Bitcoin believer, wants to help 70% unbanked locals.
He intended to give the citizens a way to save money and cut the country's $200 million remittance cost.
Transfer and deposit costs.
This makes logical sense when the president’s theatrics don’t blind you.
El Salvador's Bukele revealed plans to make bitcoin legal tender.
Remittances total $5.9 billion (23%) of the country's expenses.
Anything that reduces costs could boost the economy.
The country’s unbanked population is staggering. Here’s the data by % of people who either have a bank account (Blue) or a mobile money account (Black).
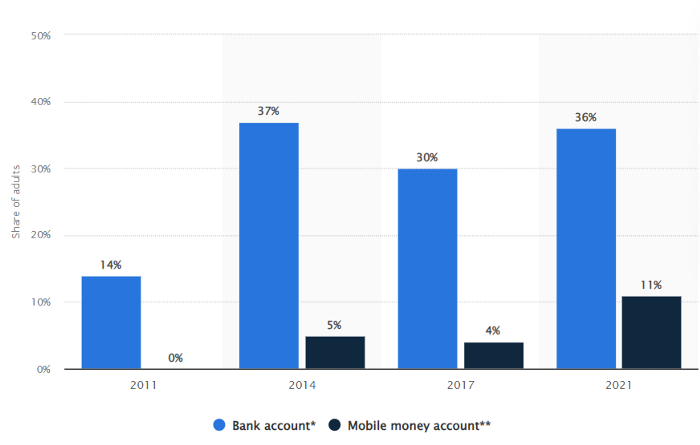
According to Bukele, 46% of the population has downloaded the Chivo Bitcoin Wallet.
In 2021, 36% of El Salvadorans had bank accounts.
Large rural countries like Kenya seem to have resolved their unbanked dilemma.
An economy surfaced where village locals would sell, trade and store network minutes and data as a store of value.
Kenyan phone networks realized unbanked people needed a safe way to accumulate wealth and have an emergency fund.
96% of Kenyans utilize M-PESA, which doesn't require a bank account.
The software involves human agents who hang out with cash and a phone.
These people are like ATMs.
You offer them cash to deposit money in your mobile money account or withdraw cash.
In a country with a faulty banking system, cash availability and a safe place to deposit it are important.
William Jack and Tavneet Suri found that M-PESA brought 194,000 Kenyan households out of poverty by making transactions cheaper and creating a safe store of value.
Mobile money, a service that allows monetary value to be stored on a mobile phone and sent to other users via text messages, has been adopted by most Kenyan households. We estimate that access to the Kenyan mobile money system M-PESA increased per capita consumption levels and lifted 194,000 households, or 2% of Kenyan households, out of poverty.
The impacts, which are more pronounced for female-headed households, appear to be driven by changes in financial behaviour — in particular, increased financial resilience and saving. Mobile money has therefore increased the efficiency of the allocation of consumption over time while allowing a more efficient allocation of labour, resulting in a meaningful reduction of poverty in Kenya.
Currently, El Salvador has 2,301 Bitcoin.
At publication, it's worth $44 million. That remains 41% of Bukele's original $105.6 million.
Unknown if the country has sold Bitcoin, but Bukeles keeps purchasing the dip.
It's still falling.

This might be a fantastic move for the impoverished country over the next five years, if they can live economically till Bitcoin's price recovers.
The evidence demonstrates that a store of value pulls individuals out of poverty, but others say Bitcoin is premature.
You may regard it as an aggressive endeavor to front run the next wave of adoption, offering El Salvador a financial upside.
You might also like

Alexandra Walker-Jones
3 years ago
These are the 15 foods you should eat daily and why.
Research on preventing disease, extending life, and caring for your body from the inside out

Grapefruit and pomegranates aren't on the list, so ignore that. Mostly, I enjoyed the visual, but those fruits are healthful, too.
15 (or 17 if you consider the photo) different foods a day sounds like a lot. If you're not used to it — it is.
These lists don't aim for perfection. Instead, use this article and the science below to eat more of these foods. If you can eat 5 foods one day and 5 the next, you're doing well. This list should be customized to your requirements and preferences.
“Every time you eat or drink, you are either feeding disease or fighting it” -Heather Morgan.
The 15 Foods That You Should Consume Daily and Why:
1. Dark/Red Berries
(blueberries, blackberries, acai, goji, cherries, strawberries, raspberries)
The 2010 Global Burden of Disease Study is the greatest definitive analysis of death and disease risk factors in history. They found the primary cause of both death, disability, and disease inside the United States was diet.
Not eating enough fruit, and specifically berries, was one of the best predictors of disease (1).
What's special about berries? It's their color! Berries have the most antioxidants of any fruit, second only to spices. The American Cancer Society found that those who ate the most berries were less likely to die of cardiovascular disease.
2. Beans
Soybeans, black beans, kidney beans, lentils, split peas, chickpeas.
Beans are one of the most important predictors of survival in older people, according to global research (2).
For every 20 grams (2 tablespoons) of beans consumed daily, the risk of death is reduced by 8%.
Soybeans and soy foods are high in phytoestrogen, which reduces breast and prostate cancer risks. Phytoestrogen blocks the receptors' access to true estrogen, mitigating the effects of weight gain, dairy (high in estrogen), and hormonal fluctuations (3).
3. Nuts
(almonds, walnuts, pecans, pistachios, Brazil nuts, cashews, hazelnuts, macadamia nuts)
Eating a handful of nuts every day reduces the risk of chronic diseases like heart disease and diabetes. Nuts also reduce oxidation, blood sugar, and LDL (bad) cholesterol, improving arterial function (4).
Despite their high-fat content, studies have linked daily nut consumption to a slimmer waistline and a lower risk of obesity (5).
4. Flaxseed
(milled flaxseed)
2013 research found that ground flaxseed had one of the strongest anti-hypertensive effects of any food. A few tablespoons (added to a smoothie or baked goods) lowered blood pressure and stroke risk 23 times more than daily aerobic exercise (6).
Flax shouldn't replace exercise, but its nutritional punch is worth adding to your diet.
5. Other seeds
(chia seeds, hemp seeds, pumpkin seeds, sesame seeds, fennel seeds)
Seeds are high in fiber and omega-3 fats and can be added to most dishes without being noticed.
When eaten with or after a meal, chia seeds moderate blood sugar and reduce inflammatory chemicals in the blood (7). Overall, a great daily addition.
6. Dates
Dates are one of the world's highest sugar foods, with 80% sugar by weight. Pure cake frosting is 60%, maple syrup is 66%, and cotton-candy jelly beans are 70%.
Despite their high sugar content, dates have a low glycemic index, meaning they don't affect blood sugar levels dramatically. They also improve triglyceride and antioxidant stress levels (8).
Dates are a great source of energy and contain high levels of dietary fiber and polyphenols, making 3-10 dates a great way to fight disease, support gut health with prebiotics, and satisfy a sweet tooth (9).
7. Cruciferous Veggies
(broccoli, Brussel sprouts, horseradish, kale, cauliflower, cabbage, boy choy, arugula, radishes, turnip greens)
Cruciferous vegetables contain an active ingredient that makes them disease-fighting powerhouses. Sulforaphane protects our brain, eyesight, against free radicals and environmental hazards, and treats and prevents cancer (10).
Unless you eat raw cruciferous vegetables daily, you won't get enough sulforaphane (and thus, its protective nutritional benefits). Cooking destroys the enzyme needed to create this super-compound.
If you chop broccoli, cauliflower, or turnip greens and let them sit for 45 minutes before cooking them, the enzyme will have had enough time to work its sulforaphane magic, allowing the vegetables to retain the same nutritional value as if eaten raw. Crazy, right? For more on this, see What Chopping Your Vegetables Has to Do with Fighting Cancer.
8. Whole grains
(barley, brown rice, quinoa, oats, millet, popcorn, whole-wheat pasta, wild rice)
Whole-grains are one of the healthiest ways to consume your daily carbs and help maintain healthy gut flora.
This happens when fibre is broken down in the colon and starts a chain reaction, releasing beneficial substances into the bloodstream and reducing the risk of Type 2 Diabetes and inflammation (11).
9. Spices
(turmeric, cumin, cinnamon, ginger, saffron, cloves, cardamom, chili powder, nutmeg, coriander)
7% of a person's cells will have DNA damage. This damage is caused by tiny breaks in our DNA caused by factors like free-radical exposure.
Free radicals cause mutations that damage lipids, proteins, and DNA, increasing the risk of disease and cancer. Free radicals are unavoidable because they result from cellular metabolism, but they can be avoided by consuming anti-oxidant and detoxifying foods.
Including spices and herbs like rosemary or ginger in our diet may cut DNA damage by 25%. Yes, this damage can be improved through diet. Turmeric worked better at a lower dose (just a pinch, daily). For maximum free-radical fighting (and anti-inflammatory) effectiveness, use 1.5 tablespoons of similar spices (12).
10. Leafy greens
(spinach, collard greens, lettuce, other salad greens, swiss chard)
Studies show that people who eat more leafy greens perform better on cognitive tests and slow brain aging by a year or two (13).
As we age, blood flow to the brain drops due to a decrease in nitric oxide, which prevents blood vessels from dilatation. Daily consumption of nitrate-rich vegetables like spinach and swiss chard may prevent dementia and Alzheimer's.
11. Fermented foods
(sauerkraut, tempeh, kombucha, plant-based kefir)
Miso, kimchi, and sauerkraut contain probiotics that support gut microbiome.
Probiotics balance the good and bad bacteria in our bodies and offer other benefits. Fermenting fruits and vegetables increases their antioxidant and vitamin content, preventing disease in multiple ways (14).
12. Sea vegetables
(seaweed, nori, dulse flakes)
A population study found that eating one sheet of nori seaweed per day may cut breast cancer risk by more than half (15).
Seaweed and sea vegetables may help moderate estrogen levels in the metabolism, reducing cancer and disease risk.
Sea vegetables make up 30% of the world's edible plants and contain unique phytonutrients. A teaspoon of these super sea-foods on your dinner will help fight disease from the inside out.
13. Water
I'm less concerned about whether you consider water food than whether you drink enough. If this list were ranked by what single item led to the best health outcomes, water would be first.
Research shows that people who drink 5 or more glasses of water per day have a 50% lower risk of dying from heart disease than those who drink 2 or less (16).
Drinking enough water boosts energy, improves skin, mental health, and digestion, and reduces the risk of various health issues, including obesity.
14. Tea
All tea consumption is linked to a lower risk of stroke, heart disease, and early death, with green tea leading for antioxidant content and immediate health benefits.
Green tea leaves may also be able to interfere with each stage of cancer formation, from the growth of the first mutated cell to the spread and progression of cancer in the body. Green tea is a quick and easy way to support your long-term and short-term health (17).
15. Supplemental B12 vitamin
B12, or cobalamin, is a vitamin responsible for cell metabolism. Not getting enough B12 can have serious consequences.
Historically, eating vegetables from untreated soil helped humans maintain their vitamin B12 levels. Due to modern sanitization, our farming soil lacks B12.
B12 is often cited as a problem only for vegetarians and vegans (as animals we eat are given B12 supplements before slaughter), but recent studies have found that plant-based eaters have lower B12 deficiency rates than any other diet (18).
Article Sources:
James Brockbank
3 years ago
Canonical URLs for Beginners
Canonicalization and canonical URLs are essential for SEO, and improper implementation can negatively impact your site's performance.
Canonical tags were introduced in 2009 to help webmasters with duplicate or similar content on multiple URLs.
To use canonical tags properly, you must understand their purpose, operation, and implementation.
Canonical URLs and Tags
Canonical tags tell search engines that a certain URL is a page's master copy. They specify a page's canonical URL. Webmasters can avoid duplicate content by linking to the "canonical" or "preferred" version of a page.
How are canonical tags and URLs different? Can these be specified differently?
Tags
Canonical tags are found in an HTML page's head></head> section.
<link rel="canonical" href="https://www.website.com/page/" />These can be self-referencing or reference another page's URL to consolidate signals.
Canonical tags and URLs are often used interchangeably, which is incorrect.
The rel="canonical" tag is the most common way to set canonical URLs, but it's not the only way.
Canonical URLs
What's a canonical link? Canonical link is the'master' URL for duplicate pages.
In Google's own words:
A canonical URL is the page Google thinks is most representative of duplicate pages on your site.
— Google Search Console Help
You can indicate your preferred canonical URL. For various reasons, Google may choose a different page than you.
When set correctly, the canonical URL is usually your specified URL.
Canonical URLs determine which page will be shown in search results (unless a duplicate is explicitly better for a user, like a mobile version).
Canonical URLs can be on different domains.
Other ways to specify canonical URLs
Canonical tags are the most common way to specify a canonical URL.
You can also set canonicals by:
Setting the HTTP header rel=canonical.
All pages listed in a sitemap are suggested as canonicals, but Google decides which pages are duplicates.
Redirects 301.
Google recommends these methods, but they aren't all appropriate for every situation, as we'll see below. Each has its own recommended uses.
Setting canonical URLs isn't required; if you don't, Google will use other signals to determine the best page version.
To control how your site appears in search engines and to avoid duplicate content issues, you should use canonicalization effectively.
Why Duplicate Content Exists
Before we discuss why you should use canonical URLs and how to specify them in popular CMSs, we must first explain why duplicate content exists. Nobody intentionally duplicates website content.
Content management systems create multiple URLs when you launch a page, have indexable versions of your site, or use dynamic URLs.
Assume the following URLs display the same content to a user:
A search engine sees eight duplicate pages, not one.
URLs #1 and #2: the CMS saves product URLs with and without the category name.
#3, #4, and #5 result from the site being accessible via HTTP, HTTPS, www, and non-www.
#6 is a subdomain mobile-friendly URL.
URL #7 lacks URL #2's trailing slash.
URL #8 uses a capital "A" instead of a lowercase one.
Duplicate content may also exist in URLs like:
https://www.website.com
https://www.website.com/index.php
Duplicate content is easy to create.
Canonical URLs help search engines identify different page variations as a single URL on many sites.
SEO Canonical URLs
Canonical URLs help you manage duplicate content that could affect site performance.
Canonical URLs are a technical SEO focus area for many reasons.
Specify URL for search results
When you set a canonical URL, you tell Google which page version to display.
Which would you click?
https://www.domain.com/page-1/
https://www.domain.com/index.php?id=2
First, probably.
Canonicals tell search engines which URL to rank.
Consolidate link signals on similar pages
When you have duplicate or nearly identical pages on your site, the URLs may get external links.
Canonical URLs consolidate multiple pages' link signals into a single URL.
This helps your site rank because signals from multiple URLs are consolidated into one.
Syndication management
Content is often syndicated to reach new audiences.
Canonical URLs consolidate ranking signals to prevent duplicate pages from ranking and ensure the original content ranks.
Avoid Googlebot duplicate page crawling
Canonical URLs ensure that Googlebot crawls your new pages rather than duplicated versions of the same one across mobile and desktop versions, for example.
Crawl budgets aren't an issue for most sites unless they have 100,000+ pages.
How to Correctly Implement the rel=canonical Tag
Using the header tag rel="canonical" is the most common way to specify canonical URLs.
Adding tags and HTML code may seem daunting if you're not a developer, but most CMS platforms allow canonicals out-of-the-box.
These URLs each have one product.
How to Correctly Implement a rel="canonical" HTTP Header
A rel="canonical" HTTP header can replace canonical tags.
This is how to implement a canonical URL for PDFs or non-HTML documents.
You can specify a canonical URL in your site's.htaccess file using the code below.
<Files "file-to-canonicalize.pdf"> Header add Link "< http://www.website.com/canonical-page/>; rel=\"canonical\"" </Files>301 redirects for canonical URLs
Google says 301 redirects can specify canonical URLs.
Only the canonical URL will exist if you use 301 redirects. This will redirect duplicates.
This is the best way to fix duplicate content across:
HTTPS and HTTP
Non-WWW and WWW
Trailing-Slash and Non-Trailing Slash URLs
On a single page, you should use canonical tags unless you can confidently delete and redirect the page.
Sitemaps' canonical URLs
Google assumes sitemap URLs are canonical, so don't include non-canonical URLs.
This does not guarantee canonical URLs, but is a best practice for sitemaps.
Best-practice Canonical Tag
Once you understand a few simple best practices for canonical tags, spotting and cleaning up duplicate content becomes much easier.
Always include:
One canonical URL per page
If you specify multiple canonical URLs per page, they will likely be ignored.
Correct Domain Protocol
If your site uses HTTPS, use this as the canonical URL. It's easy to reference the wrong protocol, so check for it to catch it early.
Trailing slash or non-trailing slash URLs
Be sure to include trailing slashes in your canonical URL if your site uses them.
Specify URLs other than WWW
Search engines see non-WWW and WWW URLs as duplicate pages, so use the correct one.
Absolute URLs
To ensure proper interpretation, canonical tags should use absolute URLs.
So use:
<link rel="canonical" href="https://www.website.com/page-a/" />And not:
<link rel="canonical" href="/page-a/" />If not canonicalizing, use self-referential canonical URLs.
When a page isn't canonicalizing to another URL, use self-referencing canonical URLs.
Canonical tags refer to themselves here.
Common Canonical Tags Mistakes
Here are some common canonical tag mistakes.
301 Canonicalization
Set the canonical URL as the redirect target, not a redirected URL.
Incorrect Domain Canonicalization
If your site uses HTTPS, don't set canonical URLs to HTTP.
Irrelevant Canonicalization
Canonicalize URLs to duplicate or near-identical content only.
SEOs sometimes try to pass link signals via canonical tags from unrelated content to increase rank. This isn't how canonicalization should be used and should be avoided.
Multiple Canonical URLs
Only use one canonical tag or URL per page; otherwise, they may all be ignored.
When overriding defaults in some CMSs, you may accidentally include two canonical tags in your page's <head>.
Pagination vs. Canonicalization
Incorrect pagination can cause duplicate content. Canonicalizing URLs to the first page isn't always the best solution.
Canonicalize to a 'view all' page.
How to Audit Canonical Tags (and Fix Issues)
Audit your site's canonical tags to find canonicalization issues.
SEMrush Site Audit can help. You'll find canonical tag checks in your website's site audit report.
Let's examine these issues and their solutions.
No Canonical Tag on AMP
Site Audit will flag AMP pages without canonical tags.
Canonicalization between AMP and non-AMP pages is important.
Add a rel="canonical" tag to each AMP page's head>.
No HTTPS redirect or canonical from HTTP homepage
Duplicate content issues will be flagged in the Site Audit if your site is accessible via HTTPS and HTTP.
You can fix this by 301 redirecting or adding a canonical tag to HTTP pages that references HTTPS.
Broken canonical links
Broken canonical links won't be considered canonical URLs.
This error could mean your canonical links point to non-existent pages, complicating crawling and indexing.
Update broken canonical links to the correct URLs.
Multiple canonical URLs
This error occurs when a page has multiple canonical URLs.
Remove duplicate tags and leave one.
Canonicalization is a key SEO concept, and using it incorrectly can hurt your site's performance.
Once you understand how it works, what it does, and how to find and fix issues, you can use it effectively to remove duplicate content from your site.
Canonicalization SEO Myths

Deon Ashleigh
3 years ago
You can dominate your daily productivity with these 9 little-known Google Calendar tips.
Calendars are great unpaid employees.
After using Notion to organize my next three months' goals, my days were a mess.
I grew very chaotic afterward. I was overwhelmed, unsure of what to do, and wasting time attempting to plan the day after it had started.
Imagine if our skeletons were on the outside. Doesn’t work.
The goals were too big; I needed to break them into smaller chunks. But how?
Enters Google Calendar
RescueTime’s recommendations took me seven hours to make a daily planner. This epic narrative begins with a sheet of paper and concludes with a daily calendar that helps me focus and achieve more goals. Ain’t nobody got time for “what’s next?” all day.
Onward!
Return to the Paleolithic Era
Plan in writing.
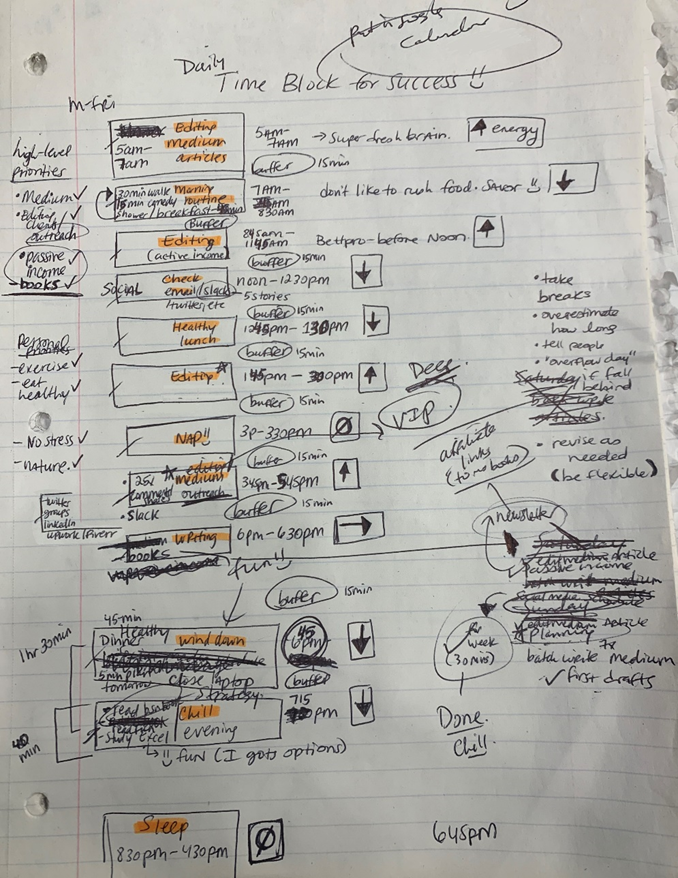
Not on the list, but it helped me plan my day. Physical writing boosts creativity and recall.
Find My Heart
i.e. prioritize
RescueTime suggested I prioritize before planning. Personal and business goals were proposed.
My top priorities are to exercise, eat healthily, spend time in nature, and avoid stress.
Priorities include writing and publishing Medium articles, conducting more freelance editing and Medium outreach, and writing/editing sci-fi books.
These eight things will help me feel accomplished every day.
Make a baby calendar.
Create daily calendar templates.
Make family, pleasure, etc. calendars.
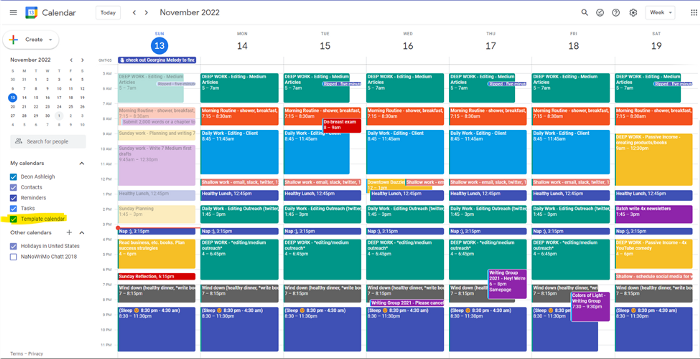
Google Calendar instructions:
Other calendars
Press the “+” button
Create a new calendar
Create recurring events for each day
My calendar, without the template:
Empty, so I can fill it with vital tasks.
With the template:

My daily skeleton corresponds with my priorities. I've been overwhelmed for years because I lack daily, weekly, monthly, and yearly structure.
Google Calendars helps me reach my goals and focus my energy.
Get your colored pencils ready
Time-block color-coding.
Color labeling lets me quickly see what's happening. Maybe you are too.
Google Calendar instructions:
Determine which colors correspond to each time block.
When establishing new events, select a color.
Save
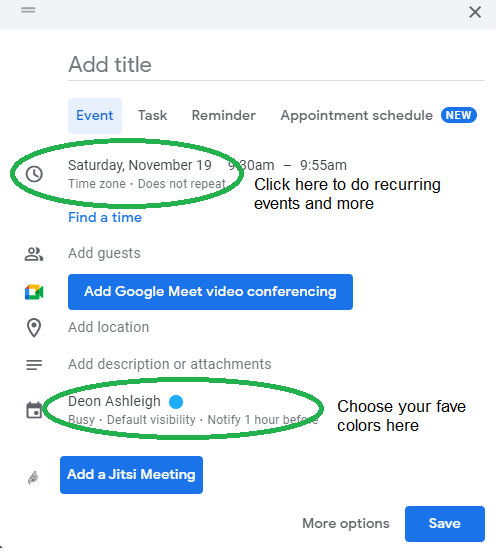
My calendar is color-coded as follows:
Yellow — passive income or other future-related activities
Red — important activities, like my monthly breast exam
Flamingo — shallow work, like emails, Twitter, etc.
Blue — all my favorite activities, like walking, watching comedy, napping, and sleeping. Oh, and eating.
Green — money-related events required for this adulting thing
Purple — writing-related stuff
Associating a time block with a color helps me stay focused. Less distractions mean faster work.
Open My Email
aka receive a daily email from Google Calendar.
Google Calendar sends a daily email feed of your calendars. I sent myself the template calendar in this email.
Google Calendar instructions:
Access settings
Select the calendar that you want to send (left side)
Go down the page to see more alerts
Under the daily agenda area, click Email.

Get in Touch With Your Red Bull Wings — Naturally
aka audit your energy levels.
My daily planner has arrows. These indicate how much energy each activity requires or how much I have.
Rightward arrow denotes medium energy.
I do my Medium and professional editing in the morning because it's energy-intensive.
Niharikaa Sodhi recommends morning Medium editing.
I’m a morning person. As long as I go to bed at a reasonable time, 5 a.m. is super wild GO-TIME. It’s like the world was just born, and I marvel at its wonderfulness.
Freelance editing lets me do what I want. An afternoon snooze will help me finish on time.
Ditch Schedule View
aka focus on the weekly view.
RescueTime advocated utilizing the weekly view of Google Calendar, so I switched.
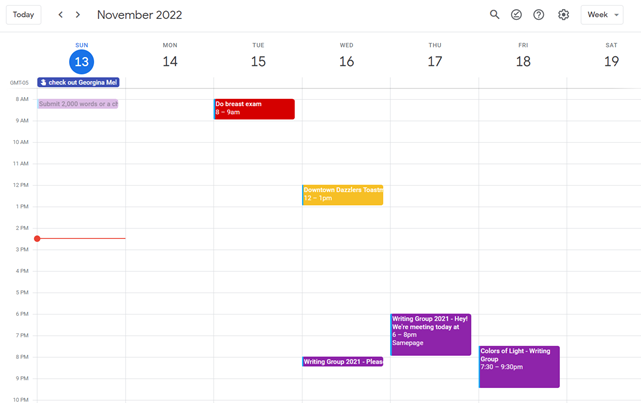
When you launch the phone app or desktop calendar, a red line shows where you are in the day.
I'll follow the red line's instructions. My digital supervisor is easy to follow.
In the image above, it's almost 3 p.m., therefore the red line implies it's time to snooze.
I won't forget this block ;).
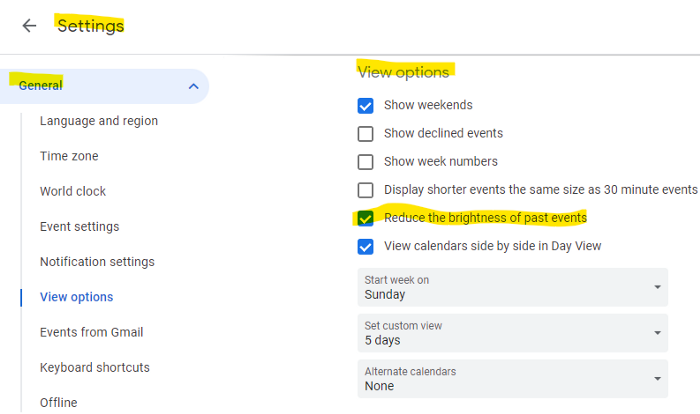
Reduce the Lighting
aka dim previous days.
This is another Google Calendar feature I didn't know about. Once the allotted time passes, the time block dims. This keeps me present.
Google Calendar instructions:
Access settings
remaining general
To view choices, click.
Check Diminish the glare of the past.
Bonus
Two additional RescueTimes hacks:
Maintain a space between tasks
I left 15 minutes between each time block to transition smoothly. This relates to my goal of less stress. If I set strict start and end times, I'll be stressed.
With a buffer, I can breathe, stroll around, and start the following time block fresh.
Find a time is related to the buffer.
This option allows you conclude small meetings five minutes early and longer ones ten. Before the next meeting, relax or go wild.
Decide on a backup day.
This productivity technique is amazing.
Spend this excess day catching up on work. It helps reduce tension and clutter.
That's all I can say about Google Calendar's functionality.
