More on Web3 & Crypto

Jonathan Vanian
4 years ago
What is Terra? Your guide to the hot cryptocurrency
With cryptocurrencies like Bitcoin, Ether, and Dogecoin gyrating in value over the past few months, many people are looking at so-called stablecoins like Terra to invest in because of their more predictable prices.
Terraform Labs, which oversees the Terra cryptocurrency project, has benefited from its rising popularity. The company said recently that investors like Arrington Capital, Lightspeed Venture Partners, and Pantera Capital have pledged $150 million to help it incubate various crypto projects that are connected to Terra.
Terraform Labs and its partners have built apps that operate on the company’s blockchain technology that helps keep a permanent and shared record of the firm’s crypto-related financial transactions.
Here’s what you need to know about Terra and the company behind it.
What is Terra?
Terra is a blockchain project developed by Terraform Labs that powers the startup’s cryptocurrencies and financial apps. These cryptocurrencies include the Terra U.S. Dollar, or UST, that is pegged to the U.S. dollar through an algorithm.
Terra is a stablecoin that is intended to reduce the volatility endemic to cryptocurrencies like Bitcoin. Some stablecoins, like Tether, are pegged to more conventional currencies, like the U.S. dollar, through cash and cash equivalents as opposed to an algorithm and associated reserve token.
To mint new UST tokens, a percentage of another digital token and reserve asset, Luna, is “burned.” If the demand for UST rises with more people using the currency, more Luna will be automatically burned and diverted to a community pool. That balancing act is supposed to help stabilize the price, to a degree.
“Luna directly benefits from the economic growth of the Terra economy, and it suffers from contractions of the Terra coin,” Terraform Labs CEO Do Kwon said.
Each time someone buys something—like an ice cream—using UST, that transaction generates a fee, similar to a credit card transaction. That fee is then distributed to people who own Luna tokens, similar to a stock dividend.
Who leads Terra?
The South Korean firm Terraform Labs was founded in 2018 by Daniel Shin and Kwon, who is now the company’s CEO. Kwon is a 29-year-old former Microsoft employee; Shin now heads the Chai online payment service, a Terra partner. Kwon said many Koreans have used the Chai service to buy goods like movie tickets using Terra cryptocurrency.
Terraform Labs does not make money from transactions using its crypto and instead relies on outside funding to operate, Kwon said. It has raised $57 million in funding from investors like HashKey Digital Asset Group, Divergence Digital Currency Fund, and Huobi Capital, according to deal-tracking service PitchBook. The amount raised is in addition to the latest $150 million funding commitment announced on July 16.
What are Terra’s plans?
Terraform Labs plans to use Terra’s blockchain and its associated cryptocurrencies—including one pegged to the Korean won—to create a digital financial system independent of major banks and fintech-app makers. So far, its main source of growth has been in Korea, where people have bought goods at stores, like coffee, using the Chai payment app that’s built on Terra’s blockchain. Kwon said the company’s associated Mirror trading app is experiencing growth in China and Thailand.
Meanwhile, Kwon said Terraform Labs would use its latest $150 million in funding to invest in groups that build financial apps on Terra’s blockchain. He likened the scouting and investing in other groups as akin to a “Y Combinator demo day type of situation,” a reference to the popular startup pitch event organized by early-stage investor Y Combinator.
The combination of all these Terra-specific financial apps shows that Terraform Labs is “almost creating a kind of bank,” said Ryan Watkins, a senior research analyst at cryptocurrency consultancy Messari.
In addition to cryptocurrencies, Terraform Labs has a number of other projects including the Anchor app, a high-yield savings account for holders of the group’s digital coins. Meanwhile, people can use the firm’s associated Mirror app to create synthetic financial assets that mimic more conventional ones, like “tokenized” representations of corporate stocks. These synthetic assets are supposed to be helpful to people like “a small retail trader in Thailand” who can more easily buy shares and “get some exposure to the upside” of stocks that they otherwise wouldn’t have been able to obtain, Kwon said. But some critics have said the U.S. Securities and Exchange Commission may eventually crack down on synthetic stocks, which are currently unregulated.
What do critics say?
Terra still has a long way to go to catch up to bigger cryptocurrency projects like Ethereum.
Most financial transactions involving Terra-related cryptocurrencies have originated in Korea, where its founders are based. Although Terra is becoming more popular in Korea thanks to rising interest in its partner Chai, it’s too early to say whether Terra-related currencies will gain traction in other countries.
Terra’s blockchain runs on a “limited number of nodes,” said Messari’s Watkins, referring to the computers that help keep the system running. That helps reduce latency that may otherwise slow processing of financial transactions, he said.
But the tradeoff is that Terra is less “decentralized” than other blockchain platforms like Ethereum, which is powered by thousands of interconnected computing nodes worldwide. That could make Terra less appealing to some blockchain purists.

Miguel Saldana
3 years ago
Crypto Inheritance's Catch-22
Security, privacy, and a strategy!

How to manage digital assets in worst-case scenarios is a perennial crypto concern. Since blockchain and bitcoin technology is very new, this hasn't been a major issue. Many early developers are still around, and many groups created around this technology are young and feel they have a lot of life remaining. This is why inheritance and estate planning in crypto should be handled promptly. As cryptocurrency's intrinsic worth rises, many people in the ecosystem are holding on to assets that might represent generational riches. With that much value, it's crucial to have a plan. Creating a solid plan entails several challenges.
the initial hesitation in coming up with a plan
The technical obstacles to ensuring the assets' security and privacy
the passing of assets from a deceased or incompetent person
Legal experts' lack of comprehension and/or understanding of how to handle and treat cryptocurrency.
This article highlights several challenges, a possible web3-native solution, and how to learn more.

The Challenge of Inheritance:
One of the biggest hurdles to inheritance planning is starting the conversation. As humans, we don't like to think about dying. Early adopters will experience crazy gains as cryptocurrencies become more popular. Creating a plan is crucial if you wish to pass on your riches to loved ones. Without a plan, the technical and legal issues I barely mentioned above would erode value by requiring costly legal fees and/or taxes, and you could lose everything if wallets and assets are not distributed appropriately (associated with the private keys). Raising awareness of the consequences of not having a plan should motivate people to make one.

Controlling Change:
Having an inheritance plan for your digital assets is crucial, but managing the guts and bolts poses a new set of difficulties. Privacy and security provided by maintaining your own wallet provide different issues than traditional finances and assets. Traditional finance is centralized (say a stock brokerage firm). You can assign another person to handle the transfer of your assets. In crypto, asset transfer is reimagined. One may suppose future transaction management is doable, but the user must consent, creating an impossible loop.
I passed away and must send a transaction to the person I intended to deliver it to.
I have to confirm or authorize the transaction, but I'm dead.
In crypto, scheduling a future transaction wouldn't function. To transfer the wallet and its contents, we'd need the private keys and/or seed phrase. Minimizing private key exposure is crucial to protecting your crypto from hackers, social engineering, and phishing. People have lost private keys after utilizing Life Hack-type tactics to secure them. People that break and hide their keys, lose them, or make them unreadable won't help with managing and/or transferring. This will require a derived solution.

Legal Challenges and Implications
Unlike routine cryptocurrency transfers and transactions, local laws may require special considerations. Even in the traditional world, estate/inheritance taxes, how assets will be split, and who executes the will must be considered. Many lawyers aren't crypto-savvy, which complicates the matter. There will be many hoops to jump through to safeguard your crypto and traditional assets and give them to loved ones.
Knowing RUFADAA/UFADAA, depending on your state, is vital for Americans. UFADAA offers executors and trustees access to online accounts (which crypto wallets would fall into). RUFADAA was changed to limit access to the executor to protect assets. RUFADAA outlines how digital assets are administered following death and incapacity in the US.
A Succession Solution
Having a will and talking about who would get what is the first step to having a solution, but using a Dad Mans Switch is a perfect tool for such unforeseen circumstances. As long as the switch's controller has control, nothing happens. Losing control of the switch initiates a state transition.
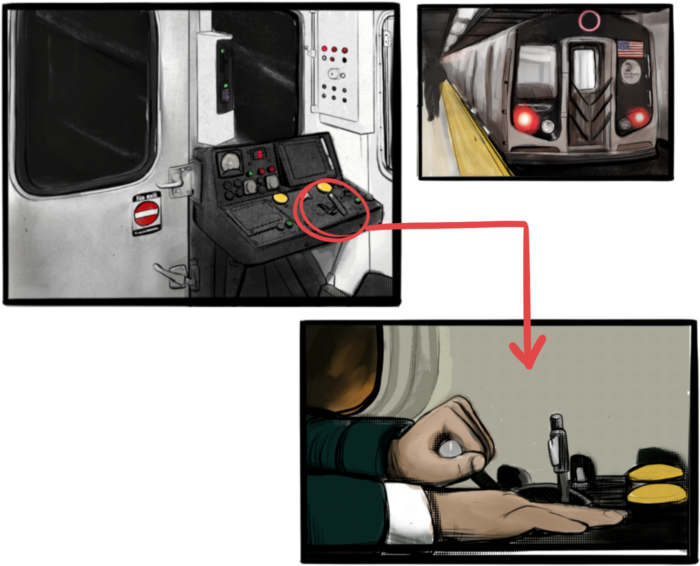
Subway or railway operations are examples. Modern control systems need the conductor to hold a switch to keep the train going. If they can't, the train stops.

Enter Sarcophagus
Sarcophagus is a decentralized dead man's switch built on Ethereum and Arweave. Sarcophagus allows actors to maintain control of their possessions even while physically unable to do so. Using a programmable dead man's switch and dual encryption, anything can be kept and passed on. This covers assets, secrets, seed phrases, and other use cases to provide authority and control back to the user and release trustworthy services from this work. Sarcophagus is built on a decentralized, transparent open source codebase. Sarcophagus is there if you're unprepared.


Ashraful Islam
4 years ago
Clean API Call With React Hooks
| Photo by Juanjo Jaramillo on Unsplash |
Calling APIs is the most common thing to do in any modern web application. When it comes to talking with an API then most of the time we need to do a lot of repetitive things like getting data from an API call, handling the success or error case, and so on.
When calling tens of hundreds of API calls we always have to do those tedious tasks. We can handle those things efficiently by putting a higher level of abstraction over those barebone API calls, whereas in some small applications, sometimes we don’t even care.
The problem comes when we start adding new features on top of the existing features without handling the API calls in an efficient and reusable manner. In that case for all of those API calls related repetitions, we end up with a lot of repetitive code across the whole application.
In React, we have different approaches for calling an API. Nowadays mostly we use React hooks. With React hooks, it’s possible to handle API calls in a very clean and consistent way throughout the application in spite of whatever the application size is. So let’s see how we can make a clean and reusable API calling layer using React hooks for a simple web application.
I’m using a code sandbox for this blog which you can get here.
import "./styles.css";
import React, { useEffect, useState } from "react";
import axios from "axios";
export default function App() {
const [posts, setPosts] = useState(null);
const [error, setError] = useState("");
const [loading, setLoading] = useState(false);
useEffect(() => {
handlePosts();
}, []);
const handlePosts = async () => {
setLoading(true);
try {
const result = await axios.get(
"https://jsonplaceholder.typicode.com/posts"
);
setPosts(result.data);
} catch (err) {
setError(err.message || "Unexpected Error!");
} finally {
setLoading(false);
}
};
return (
<div className="App">
<div>
<h1>Posts</h1>
{loading && <p>Posts are loading!</p>}
{error && <p>{error}</p>}
<ul>
{posts?.map((post) => (
<li key={post.id}>{post.title}</li>
))}
</ul>
</div>
</div>
);
}
I know the example above isn’t the best code but at least it’s working and it’s valid code. I will try to improve that later. For now, we can just focus on the bare minimum things for calling an API.
Here, you can try to get posts data from JsonPlaceholer. Those are the most common steps we follow for calling an API like requesting data, handling loading, success, and error cases.
If we try to call another API from the same component then how that would gonna look? Let’s see.
500: Internal Server Error
Now it’s going insane! For calling two simple APIs we’ve done a lot of duplication. On a top-level view, the component is doing nothing but just making two GET requests and handling the success and error cases. For each request, it’s maintaining three states which will periodically increase later if we’ve more calls.
Let’s refactor to make the code more reusable with fewer repetitions.
Step 1: Create a Hook for the Redundant API Request Codes
Most of the repetitions we have done so far are about requesting data, handing the async things, handling errors, success, and loading states. How about encapsulating those things inside a hook?
The only unique things we are doing inside handleComments and handlePosts are calling different endpoints. The rest of the things are pretty much the same. So we can create a hook that will handle the redundant works for us and from outside we’ll let it know which API to call.
500: Internal Server Error
Here, this request function is identical to what we were doing on the handlePosts and handleComments. The only difference is, it’s calling an async function apiFunc which we will provide as a parameter with this hook. This apiFunc is the only independent thing among any of the API calls we need.
With hooks in action, let’s change our old codes in App component, like this:
500: Internal Server Error
How about the current code? Isn’t it beautiful without any repetitions and duplicate API call handling things?
Let’s continue our journey from the current code. We can make App component more elegant. Now it knows a lot of details about the underlying library for the API call. It shouldn’t know that. So, here’s the next step…
Step 2: One Component Should Take Just One Responsibility
Our App component knows too much about the API calling mechanism. Its responsibility should just request the data. How the data will be requested under the hood, it shouldn’t care about that.
We will extract the API client-related codes from the App component. Also, we will group all the API request-related codes based on the API resource. Now, this is our API client:
import axios from "axios";
const apiClient = axios.create({
// Later read this URL from an environment variable
baseURL: "https://jsonplaceholder.typicode.com"
});
export default apiClient;
All API calls for comments resource will be in the following file:
import client from "./client";
const getComments = () => client.get("/comments");
export default {
getComments
};
All API calls for posts resource are placed in the following file:
import client from "./client";
const getPosts = () => client.get("/posts");
export default {
getPosts
};
Finally, the App component looks like the following:
import "./styles.css";
import React, { useEffect } from "react";
import commentsApi from "./api/comments";
import postsApi from "./api/posts";
import useApi from "./hooks/useApi";
export default function App() {
const getPostsApi = useApi(postsApi.getPosts);
const getCommentsApi = useApi(commentsApi.getComments);
useEffect(() => {
getPostsApi.request();
getCommentsApi.request();
}, []);
return (
<div className="App">
{/* Post List */}
<div>
<h1>Posts</h1>
{getPostsApi.loading && <p>Posts are loading!</p>}
{getPostsApi.error && <p>{getPostsApi.error}</p>}
<ul>
{getPostsApi.data?.map((post) => (
<li key={post.id}>{post.title}</li>
))}
</ul>
</div>
{/* Comment List */}
<div>
<h1>Comments</h1>
{getCommentsApi.loading && <p>Comments are loading!</p>}
{getCommentsApi.error && <p>{getCommentsApi.error}</p>}
<ul>
{getCommentsApi.data?.map((comment) => (
<li key={comment.id}>{comment.name}</li>
))}
</ul>
</div>
</div>
);
}
Now it doesn’t know anything about how the APIs get called. Tomorrow if we want to change the API calling library from axios to fetch or anything else, our App component code will not get affected. We can just change the codes form client.js This is the beauty of abstraction.
Apart from the abstraction of API calls, Appcomponent isn’t right the place to show the list of the posts and comments. It’s a high-level component. It shouldn’t handle such low-level data interpolation things.
So we should move this data display-related things to another low-level component. Here I placed those directly in the App component just for the demonstration purpose and not to distract with component composition-related things.
Final Thoughts
The React library gives the flexibility for using any kind of third-party library based on the application’s needs. As it doesn’t have any predefined architecture so different teams/developers adopted different approaches to developing applications with React. There’s nothing good or bad. We choose the development practice based on our needs/choices. One thing that is there beyond any choices is writing clean and maintainable codes.
You might also like

Jano le Roux
3 years ago
The Real Reason Adobe Just Paid $20 billion for Figma
Sketch or Figma?

Designers are pissed.
The beast ate the beauty.
Figma deserves $20B.
Do designers deserve Adobe?
Adobe devours new creative tools and spits them out with a slimy Adobe aftertaste.
Frame.io — $1.3B
Magento — $1.7B
Macromedia — $3.6B
Nothing compares to the risky $20B acquisition.
If they can't be beaten, buy them.
And then make them boring.
Adobe's everywhere.
Like that friend who dabbles in everything creatively, there's not enough time to master one thing.
Figma was Adobe's thigh-mounted battle axe.
a UX design instrument with a sizable free tier.
a UX design tool with a simple and quick user interface.
a tool for fluid collaboration in user experience design.
a web-based UX design tool that functions well.
a UX design tool with a singular goal of perfection.
UX design software that replaced Adobe XD.
Adobe XD could do many of Figma's things, but it didn't focus on the details. This is a major issue when working with detail-oriented professionals.
UX designers.
Design enthusiasts first used Figma. More professionals used it. Institutions taught it. Finally, major brands adopted Figma.
Adobe hated that.
Adobe dispatched a team of lawyers to resolve the Figma issue, as big companies do. Figma didn’t bite for months.
Oh no.
Figma resisted.
Figma helped designers leave Adobe. Figma couldn't replace Photoshop, but most designers used it to remove backgrounds.
Online background removal tools improved.
The Figma problem grew into a thorn, a knife, and a battle ax in Adobe's soft inner thigh.
Figma appeared to be going public. Adobe couldn’t allow that. It bought Figma for $20B during the IPO drought.
Adobe has a new issue—investors are upset.
The actual cause of investors' ire toward Adobe
Spoiler: The math just doesn’t add up.
According to Adobe's press release, Figma's annual recurring revenue (ARR) is $400M and growing rapidly.
The $20B valuation requires a 50X revenue multiple, which is unheard of.
Venture capitalists typically use:
10% to 29% growth per year: ARR multiplied by 1 to 5
30% to 99% growth per year: ARR multiplied by 6 to 10
100% to 400% growth per year: ARR multiplied by 10 to 20
Showing an investor a 50x multiple is like telling friends you saw a UFO. They'll think you're crazy.
Adobe's stock fell immediately after the acquisition because it didn't make sense to a number-cruncher.
Designers started a Tweet storm in the digital town hall where VCs and designers often meet.
Adobe acquired Workfront for $1.5 billion at the end of 2020. This purchase made sense for investors.
Many investors missed the fact that Adobe is acquiring Figma not only for its ARR but also for its brilliant collaboration tech.
Adobe could use Figmas web app technology to make more products web-based to compete with Canva.
Figma's high-profile clients could switch to Adobe's enterprise software.
However, questions arise:
Will Adobe make Figma boring?
Will Adobe tone down Figma to boost XD?
Would you ditch Adobe and Figma for Sketch?

Hudson Rennie
3 years ago
My Work at a $1.2 Billion Startup That Failed
Sometimes doing everything correctly isn't enough.

In 2020, I could fix my life.
After failing to start a business, I owed $40,000 and had no work.
A $1.2 billion startup on the cusp of going public pulled me up.
Ironically, it was getting ready for an epic fall — with the world watching.
Life sometimes helps. Without a base, even the strongest fall. A corporation that did everything right failed 3 months after going public.
First-row view.
Apple is the creator of Adore.
Out of respect, I've altered the company and employees' names in this account, despite their failure.
Although being a publicly traded company, it may become obvious.
We’ll call it “Adore” — a revolutionary concept in retail shopping.
Two Apple execs established Adore in 2014 with a focus on people-first purchasing.
Jon and Tim:
The concept for the stylish Apple retail locations you see today was developed by retail expert Jon Swanson, who collaborated closely with Steve Jobs.
Tim Cruiter is a graphic designer who produced the recognizable bouncing lamp video that appears at the start of every Pixar film.
The dynamic duo realized their vision.
“What if you could combine the convenience of online shopping with the confidence of the conventional brick-and-mortar store experience.”
Adore's mobile store concept combined traditional retail with online shopping.
Adore brought joy to 70+ cities and 4 countries over 7 years, including the US, Canada, and the UK.
Being employed on the ground floor, with world dominance and IPO on the horizon, was exciting.
I started as an Adore Expert.
I delivered cell phones, helped consumers set them up, and sold add-ons.
As the company grew, I became a Virtual Learning Facilitator and trained new employees across North America using Zoom.
In this capacity, I gained corporate insider knowledge. I worked with the creative team and Jon and Tim.
It's where I saw company foundation fissures. Despite appearances, investors were concerned.
The business strategy was ground-breaking.
Even after seeing my employee stocks fall from a home down payment to $0 (when Adore filed for bankruptcy), it's hard to pinpoint what went wrong.
Solid business model, well-executed.
Jon and Tim's chase for public funding ended in glory.
Here’s the business model in a nutshell:
Buying cell phones is cumbersome. You have two choices:
Online purchase: not knowing what plan you require or how to operate your device.
Enter a store, which can be troublesome and stressful.
Apple, AT&T, and Rogers offered Adore as a free delivery add-on. Customers could:
Have their phone delivered by UPS or Canada Post in 1-2 weeks.
Alternately, arrange for a person to visit them the same day (or sometimes even the same hour) to assist them set up their phone and demonstrate how to use it (transferring contacts, switching the SIM card, etc.).
Each Adore Expert brought a van with extra devices and accessories to customers.
Happy customers.
Here’s how Adore and its partners made money:
Adores partners appreciated sending Experts to consumers' homes since they improved customer satisfaction, average sale, and gadget returns.
**Telecom enterprises have low customer satisfaction. The average NPS is 30/100. Adore's global NPS was 80.
Adore made money by:
a set cost for each delivery
commission on sold warranties and extras
Consumer product applications seemed infinite.
A proprietary scheduling system (“The Adore App”), allowed for same-day, even same-hour deliveries.
It differentiates Adore.
They treated staff generously by:
Options on stock
health advantages
sales enticements
high rates per hour
Four-day workweeks were set by experts.
Being hired early felt like joining Uber, Netflix, or Tesla. We hoped the company's stocks would rise.
Exciting times.
I smiled as I greeted more than 1,000 new staff.
I spent a decade in retail before joining Adore. I needed a change.
After a leap of faith, I needed a lifeline. So, I applied for retail sales jobs in the spring of 2019.
The universe typically offers you what you want after you accept what you need. I needed a job to settle my debt and reach $0 again.
And the universe listened.
After being hired as an Adore Expert, I became a Virtual Learning Facilitator. Enough said.
After weeks of economic damage from the pandemic.
This employment let me work from home during the pandemic. It taught me excellent business skills.
I was active in brainstorming, onboarding new personnel, and expanding communication as we grew.
This job gave me vital skills and a regular paycheck during the pandemic.
It wasn’t until January of 2022 that I left on my own accord to try to work for myself again — this time, it’s going much better.
Adore was perfect. We valued:
Connection
Discovery
Empathy
Everything we did centered on compassion, and we held frequent Justice Calls to discuss diversity and work culture.
The last day of onboarding typically ended in tears as employees felt like they'd found a home, as I had.
Like all nice things, the wonderful vibes ended.
First indication of distress
My first day at the workplace was great.
Fun, intuitive, and they wanted creative individuals, not salesman.
While sales were important, the company's vision was more important.
“To deliver joy through life-changing mobile retail experiences.”
Thorough, forward-thinking training. We had a module on intuition. It gave us role ownership.
We were flown cross-country for training, gave feedback, and felt like we made a difference. Multiple contacts responded immediately and enthusiastically.
The atmosphere was genuine.
Making money was secondary, though. Incredible service was a priority.
Jon and Tim answered new hires' questions during Zoom calls during onboarding. CEOs seldom meet new hires this way, but they seemed to enjoy it.
All appeared well.
But in late 2021, things started changing.
Adore's leadership changed after its IPO. From basic values to sales maximization. We lost communication and were forced to fend for ourselves.
Removed the training wheels.
It got tougher to gain instructions from those above me, and new employees told me their roles weren't as advertised.
External money-focused managers were hired.
Instead of creative types, we hired salespeople.
With a new focus on numbers, Adore's uniqueness began to crumble.
Via Zoom, hundreds of workers were let go.
So.
Early in 2022, mass Zoom firings were trending. A CEO firing 900 workers over Zoom went viral.
Adore was special to me, but it became a headline.
30 June 2022, Vice Motherboard published Watch as Adore's CEO Fires Hundreds.
It described a leaked video of Jon Swanson laying off all staff in Canada and the UK.
They called it a “notice of redundancy”.
The corporation couldn't pay its employees.
I loved Adore's underlying ideals, among other things. We called clients Adorers and sold solutions, not add-ons.
But, like anything, a company is only as strong as its weakest link. And obviously, the people-first focus wasn’t making enough money.
There were signs. The expansion was presumably a race against time and money.
Adore finally declared bankruptcy.
Adore declared bankruptcy 3 months after going public. It happened in waves, like any large-scale fall.
Initial key players to leave were
Then, communication deteriorated.
Lastly, the corporate culture disintegrated.
6 months after leaving Adore, I received a letter in the mail from a Law firm — it was about my stocks.
Adore filed Chapter 11. I had to sue to collect my worthless investments.
I hoped those stocks will be valuable someday. Nope. Nope.
Sad, I sighed.
$1.2 billion firm gone.
I left the workplace 3 months before starting a writing business. Despite being mediocre, I'm doing fine.
I got up as Adore fell.
Finally, can we scale kindness?
I trust my gut. Changes at Adore made me leave before it sank.
Adores' unceremonious slide from a top startup to bankruptcy is astonishing to me.
The company did everything perfectly, in my opinion.
first to market,
provided excellent service
paid their staff handsomely.
was responsible and attentive to criticism
The company wasn't led by an egotistical eccentric. The crew had centuries of cumulative space experience.
I'm optimistic about the future of work culture, but is compassion scalable?
Blake Montgomery
3 years ago
Explaining Twitter Files
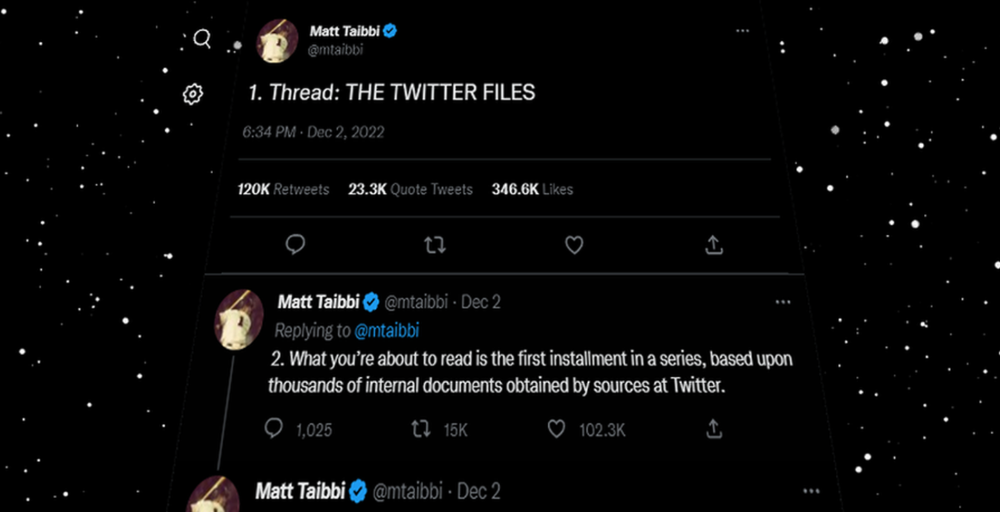
Elon Musk, Matt Taibbi, the 'Twitter Files,' and Hunter Biden's laptop: what gives?
Explaining Twitter Files
Matt Taibbi released "The Twitter Files," a batch of emails sent by Twitter executives discussing the company's decision to stop an October 2020 New York Post story online.
What's on Twitter? New York Post and Fox News call them "bombshell" documents. Or, as a Post columnist admitted, are they "not the smoking gun"? Onward!
What started this?
The New York Post published an exclusive, potentially explosive story in October 2020: Biden's Secret Emails: Ukrainian executive thanks Hunter Biden for'meeting' veep dad. The story purported to report the contents of a laptop brought to the tabloid by a Delaware computer repair shop owner who said it belonged to President Biden's second son, Hunter Biden. Emails and files on the laptop allegedly showed how Hunter peddled influence with Ukranian businessmen and included a "raunchy 12-minute video" of Hunter smoking crack and having sex.
Twitter banned links to the Post story after it was published, calling it "hacked material." The Post's Twitter account was suspended for multiple days.
Why? Yoel Roth, Twitter's former head of trust and safety, said the company couldn't verify the story, implying they didn't trust the Post.
Twitter's stated purpose rarely includes verifying news stories. This seemed like intentional political interference. This story was hard to verify because the people who claimed to have found the laptop wouldn't give it to other newspapers. (Much of the story, including Hunter's business dealings in Ukraine and China, was later confirmed.)
Roth: "It looked like a hack and leak."
So what are the “Twitter Files?”
Twitter's decision to bury the story became a political scandal, and new CEO Elon Musk promised an explanation. The Twitter Files, named after Facebook leaks.
Musk promised exclusive details of "what really happened" with Hunter Biden late Friday afternoon. The tweet was punctuated with a popcorn emoji.
Explaining Twitter Files
Three hours later, journalist Matt Taibbi tweeted more than three dozen tweets based on internal Twitter documents that revealed "a Frankensteinian tale of a human-built mechanism grown out of its designer's control."
Musk sees this release as a way to shape Twitter's public perception and internal culture in his image. We don't know if the CEO gave Taibbi the documents. Musk hyped the document dump before and during publication, but Taibbi cited "internal sources."
Taibbi shares email screenshots showing Twitter execs discussing the Post story and blocking its distribution. Taibbi says the emails show Twitter's "extraordinary steps" to bury the story.
Twitter communications chief Brandon Borrman has the most damning quote in the Files. Can we say this is policy? The story seemed unbelievable. It seemed like a hack... or not? Could Twitter, which ex-CEO Dick Costolo called "the free speech wing of the free speech party," censor a news story?
Many on the right say the Twitter Files prove the company acted at the behest of Democrats. Both parties had these tools, writes Taibbi. In 2020, both the Trump White House and Biden campaign made requests. He says the system for reporting tweets for deletion is unbalanced because Twitter employees' political donations favor Democrats. Perhaps. These donations may have helped Democrats connect with Twitter staff, but it's also possible they didn't. No emails in Taibbi's cache show these alleged illicit relations or any actions Twitter employees took as a result.
Even Musk's supporters were surprised by the drop. Miranda Devine of the New York Post told Tucker Carlson the documents weren't "the smoking gun we'd hoped for." Sebastian Gorka said on Truth Social, "So far, I'm deeply underwhelmed." DC Democrats collude with Palo Alto Democrats. Whoop!” The Washington Free Beacon's Joe Simonson said the Twitter files are "underwhelming." Twitter was staffed by Democrats who did their bidding. (Why?)
If "The Twitter Files" matter, why?
These emails led Twitter to suppress the Hunter Biden laptop story has real news value. It's rare for a large and valuable company like Twitter to address wrongdoing so thoroughly. Emails resemble FOIA documents. They describe internal drama at a company with government-level power. Katie Notopoulos tweeted, "Any news outlet would've loved this scoop!" It's not a'scandal' as teased."
Twitter's new owner calls it "the de facto public town square," implying public accountability. Like a government agency. Though it's exciting to receive once-hidden documents in response to a FOIA, they may be boring and tell you nothing new. Like Twitter files. We learned how Twitter blocked the Post's story, but not why. Before these documents were released, we knew Twitter had suppressed the story and who was involved.
These people were disciplined and left Twitter. Musk fired Vijaya Gadde, the former CLO who reportedly played a "key role" in the decision. Roth quit over Musk's "dictatorship." Musk arrived after Borrman left. Jack Dorsey, then-CEO, has left. Did those who digitally quarantined the Post's story favor Joe Biden and the Democrats? Republican Party opposition and Trump hatred? New York Post distaste? According to our documents, no. Was there political and press interference? True. We knew.
Taibbi interviewed anonymous ex-Twitter employees about the decision; all expressed shock and outrage. One source said, "Everyone knew this was fucked." Since Taibbi doesn't quote that expletive, we can assume the leaked emails contained few or no sensational quotes. These executives said little to support nefarious claims.
Outlets more invested in the Hunter Biden story than Gizmodo seem vexed by the release and muted headlines. The New York Post, which has never shied away from a blaring headline in its 221-year history, owns the story of Hunter Biden's laptop. Two Friday-night Post alerts about Musk's actions were restrained. Elon Musk will drop Twitter files on NY Post-Hunter Biden laptop censorship today. Elon Musk's Twitter dropped Post censorship details from Biden's laptop. Fox News' Apple News push alert read, "Elon Musk drops Twitter censorship documents."
Bombshell, bombshell, bombshell… what, exactly, is the bombshell? Maybe we've heard this story too much and are missing the big picture. Maybe these documents detail a well-documented decision.
The Post explains why on its website. "Hunter Biden laptop bombshell: Twitter invented reason to censor Post's reporting," its headline says.
Twitter's ad hoc decision to moderate a tabloid's content is not surprising. The social network had done this for years as it battled toxic users—violent white nationalists, virulent transphobes, harassers and bullies of all political stripes, etc. No matter how much Musk crows, the company never had content moderation under control. Buzzfeed's 2016 investigation showed how Twitter has struggled with abusive posters since 2006. Jack Dorsey and his executives improvised, like Musk.
Did the US government interfere with the ex-social VP's media company? That's shocking, a bombshell. Musk said Friday, "Twitter suppressing free speech by itself is not a 1st amendment violation, but acting under government orders with no judicial review is." Indeed! Taibbi believed this. August 2022: "The laptop is secondary." Zeynep Tufecki, a Columbia professor and New York Times columnist, says the FBI is cutting true story distribution. Taibbi retracted the claim Friday night: "I've seen no evidence of government involvement in the laptop story."
What’s the bottom line?
I'm still not sure what's at stake in the Hunter Biden scandal after dozens of New York Post articles, hundreds of hours of Fox News airtime, and thousands of tweets. Briefly: Joe Biden's son left his laptop with a questionable repairman. FBI confiscated it? The repairman made a copy and gave it to Rudy Giuliani's lawyer. The Post got it from Steve Bannon. On that laptop were videos of Hunter Biden smoking crack, cavorting with prostitutes, and emails about introducing his father to a Ukrainian businessman for $50,000 a month. Joe Biden urged Ukraine to fire a prosecutor investigating the company. What? The story seems to be about Biden family business dealings, right?
The discussion has moved past that point anyway. Now, the story is the censorship of it. Adrienne Rich wrote in "Diving Into the Wreck" that she came for "the wreck and not the story of the wreck" No matter how far we go, Hunter Biden's laptop is done. Now, the crash's story matters.
I'm dizzy. Katherine Miller of BuzzFeed wrote, "I know who I believe, and you probably do, too. To believe one is to disbelieve the other, which implicates us in the decision; we're stuck." I'm stuck. Hunter Biden's laptop is a political fabrication. You choose. I've decided.
This could change. Twitter Files drama continues. Taibbi said, "Much more to come." I'm dizzy.
