An approximate introduction to how zk-SNARKs are possible (part 1)
You can make a proof for the statement "I know a secret number such that if you take the word ‘cow', add the number to the end, and SHA256 hash it 100 million times, the output starts with 0x57d00485aa". The verifier can verify the proof far more quickly than it would take for them to run 100 million hashes themselves, and the proof would also not reveal what the secret number is.
In the context of blockchains, this has 2 very powerful applications: Perhaps the most powerful cryptographic technology to come out of the last decade is general-purpose succinct zero knowledge proofs, usually called zk-SNARKs ("zero knowledge succinct arguments of knowledge"). A zk-SNARK allows you to generate a proof that some computation has some particular output, in such a way that the proof can be verified extremely quickly even if the underlying computation takes a very long time to run. The "ZK" part adds an additional feature: the proof can keep some of the inputs to the computation hidden.
You can make a proof for the statement "I know a secret number such that if you take the word ‘cow', add the number to the end, and SHA256 hash it 100 million times, the output starts with 0x57d00485aa". The verifier can verify the proof far more quickly than it would take for them to run 100 million hashes themselves, and the proof would also not reveal what the secret number is.
In the context of blockchains, this has two very powerful applications:
- Scalability: if a block takes a long time to verify, one person can verify it and generate a proof, and everyone else can just quickly verify the proof instead
- Privacy: you can prove that you have the right to transfer some asset (you received it, and you didn't already transfer it) without revealing the link to which asset you received. This ensures security without unduly leaking information about who is transacting with whom to the public.
But zk-SNARKs are quite complex; indeed, as recently as in 2014-17 they were still frequently called "moon math". The good news is that since then, the protocols have become simpler and our understanding of them has become much better. This post will try to explain how ZK-SNARKs work, in a way that should be understandable to someone with a medium level of understanding of mathematics.
Why ZK-SNARKs "should" be hard
Let us take the example that we started with: we have a number (we can encode "cow" followed by the secret input as an integer), we take the SHA256 hash of that number, then we do that again another 99,999,999 times, we get the output, and we check what its starting digits are. This is a huge computation.
A "succinct" proof is one where both the size of the proof and the time required to verify it grow much more slowly than the computation to be verified. If we want a "succinct" proof, we cannot require the verifier to do some work per round of hashing (because then the verification time would be proportional to the computation). Instead, the verifier must somehow check the whole computation without peeking into each individual piece of the computation.
One natural technique is random sampling: how about we just have the verifier peek into the computation in 500 different places, check that those parts are correct, and if all 500 checks pass then assume that the rest of the computation must with high probability be fine, too?
Such a procedure could even be turned into a non-interactive proof using the Fiat-Shamir heuristic: the prover computes a Merkle root of the computation, uses the Merkle root to pseudorandomly choose 500 indices, and provides the 500 corresponding Merkle branches of the data. The key idea is that the prover does not know which branches they will need to reveal until they have already "committed to" the data. If a malicious prover tries to fudge the data after learning which indices are going to be checked, that would change the Merkle root, which would result in a new set of random indices, which would require fudging the data again... trapping the malicious prover in an endless cycle.
But unfortunately there is a fatal flaw in naively applying random sampling to spot-check a computation in this way: computation is inherently fragile. If a malicious prover flips one bit somewhere in the middle of a computation, they can make it give a completely different result, and a random sampling verifier would almost never find out.
It only takes one deliberately inserted error, that a random check would almost never catch, to make a computation give a completely incorrect result.
If tasked with the problem of coming up with a zk-SNARK protocol, many people would make their way to this point and then get stuck and give up. How can a verifier possibly check every single piece of the computation, without looking at each piece of the computation individually? There is a clever solution.
see part 2
(Edited)
More on Web3 & Crypto

Nabil Alouani
3 years ago
Why Cryptocurrency Is Not Dead Despite the FTX Scam
A fraud, free-market, antifragility tale

Crypto's only rival is public opinion.
In less than a week, mainstream media, bloggers, and TikTokers turned on FTX's founder.
While some were surprised, almost everyone with a keyboard and a Twitter account predicted the FTX collapse. These financial oracles should have warned the 1.2 million people Sam Bankman-Fried duped.
After happening, unexpected events seem obvious to our brains. It's a bug and a feature because it helps us cope with disasters and makes our reasoning suck.
Nobody predicted the FTX debacle. Bloomberg? Politicians. Non-famous. No cryptologists. Who?
When FTX imploded, taking billions of dollars with it, an outrage bomb went off, and the resulting shockwave threatens the crypto market's existence.
As someone who lost more than $78,000 in a crypto scam in 2020, I can only understand people’s reactions. When the dust settles and rationality returns, we'll realize this is a natural occurrence in every free market.
What specifically occurred with FTX? (Skip if you are aware.)
FTX is a cryptocurrency exchange where customers can trade with cash. It reached #3 in less than two years as the fastest-growing platform of its kind.
FTX's performance helped make SBF the crypto poster boy. Other reasons include his altruistic public image, his support for the Democrats, and his company Alameda Research.
Alameda Research made a fortune arbitraging Bitcoin.
Arbitrage trading uses small price differences between two markets to make money. Bitcoin costs $20k in Japan and $21k in the US. Alameda Research did that for months, making $1 million per day.
Later, as its capital grew, Alameda expanded its trading activities and began investing in other companies.
Let's now discuss FTX.
SBF's diabolic master plan began when he used FTX-created FTT coins to inflate his trading company's balance sheets. He used inflated Alameda numbers to secure bank loans.
SBF used money he printed himself as collateral to borrow billions for capital. Coindesk exposed him in a report.
One of FTX's early investors tweeted that he planned to sell his FTT coins over the next few months. This would be a minor event if the investor wasn't Binance CEO Changpeng Zhao (CZ).
The crypto space saw a red WARNING sign when CZ cut ties with FTX. Everyone with an FTX account and a brain withdrew money. Two events followed. FTT fell from $20 to $4 in less than 72 hours, and FTX couldn't meet withdrawal requests, spreading panic.
SBF reassured FTX users on Twitter. Good assets.
He lied.
SBF falsely claimed FTX had a liquidity crunch. At the time of his initial claims, FTX owed about $8 billion to its customers. Liquidity shortages are usually minor. To get cash, sell assets. In the case of FTX, the main asset was printed FTT coins.
Sam wouldn't get out of trouble even if he slashed the discount (from $20 to $4) and sold every FTT. He'd flood the crypto market with his homemade coins, causing the price to crash.
SBF was trapped. He approached Binance about a buyout, which seemed good until Binance looked at FTX's books.
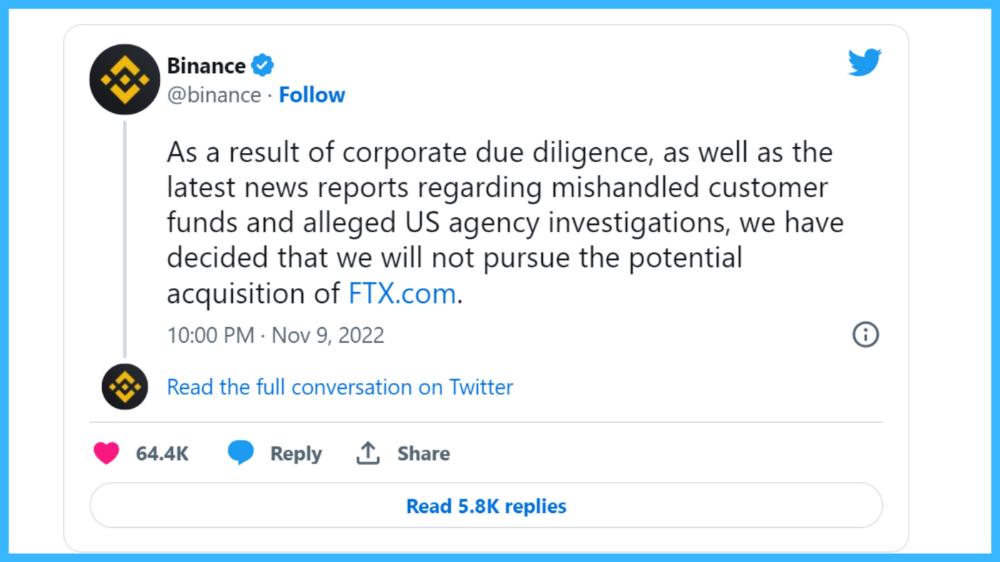
Binance's tweet ended SBF, and he had to apologize, resign as CEO, and file for bankruptcy.
Bloomberg estimated Sam's net worth to be zero by the end of that week. 0!
But that's not all. Twitter investigations exposed fraud at FTX and Alameda Research. SBF used customer funds to trade and invest in other companies.
Thanks to the Twitter indie reporters who made the mainstream press look amateurish. Some Twitter detectives didn't sleep for 30 hours to find answers. Others added to existing threads. Memes were hilarious.
One question kept repeating in my bald head as I watched the Blue Bird. Sam, WTF?
Then I understood.
SBF wanted that FTX becomes a bank.
Think about this. FTX seems healthy a few weeks ago. You buy 2 bitcoins using FTX. You'd expect the platform to take your dollars and debit your wallet, right?
No. They give I-Owe-Yous.
FTX records owing you 2 bitcoins in its internal ledger but doesn't credit your account. Given SBF's tricks, I'd bet on nothing.
What happens if they don't credit my account with 2 bitcoins? Your money goes into FTX's capital, where SBF and his friends invest in marketing, political endorsements, and buying other companies.
Over its two-year existence, FTX invested in 130 companies. Once they make a profit on their purchases, they'll pay you and keep the rest.
One detail makes their strategy dumb. If all FTX customers withdraw at once, everything collapses.
Financially savvy people think FTX's collapse resembles a bank run, and they're right. SBF designed FTX to operate like a bank.
You expect your bank to open a drawer with your name and put $1,000 in it when you deposit $1,000. They deposit $100 in your drawer and create an I-Owe-You for $900. What happens to $900?
Let's sum it up: It's boring and headache-inducing.
When you deposit money in a bank, they can keep 10% and lend the rest. Fractional Reserve Banking is a popular method. Fractional reserves operate within and across banks.
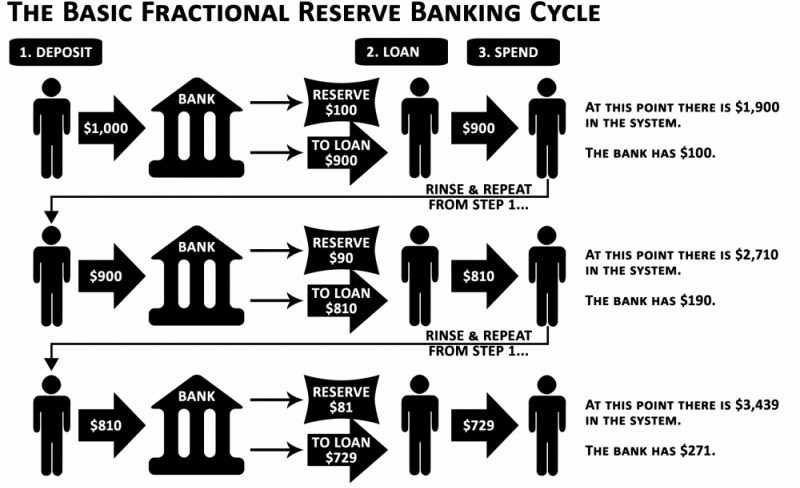
Fractional reserve banking generates $10,000 for every $1,000 deposited. People will pay off their debt plus interest.
As long as banks work together and the economy grows, their model works well.
SBF tried to replicate the system but forgot two details. First, traditional banks need verifiable collateral like real estate, jewelry, art, stocks, and bonds, not digital coupons. Traditional banks developed a liquidity buffer. The Federal Reserve (or Central Bank) injects massive cash into troubled banks.
Massive cash injections come from taxpayers. You and I pay for bankers' mistakes and annual bonuses. Yes, you may think banking is rigged. It's rigged, but it's the best financial game in 150 years. We accept its flaws, including bailouts for too-big-to-fail companies.
Anyway.
SBF wanted Binance's bailout. Binance said no, which was good for the crypto market.
Free markets are resilient.
Nassim Nicholas Taleb coined the term antifragility.
“Some things benefit from shocks; they thrive and grow when exposed to volatility, randomness, disorder, and stressors and love adventure, risk, and uncertainty. Yet, in spite of the ubiquity of the phenomenon, there is no word for the exact opposite of fragile. Let us call it antifragile. Antifragility is beyond resilience or robustness. The resilient resists shocks and stays the same; the antifragile gets better.”
The easiest way to understand how antifragile systems behave is to compare them with other types of systems.
Glass is like a fragile system. It snaps when shocked.
Similar to rubber, a resilient system. After a stressful episode, it bounces back.
A system that is antifragile is similar to a muscle. As it is torn in the gym, it gets stronger.
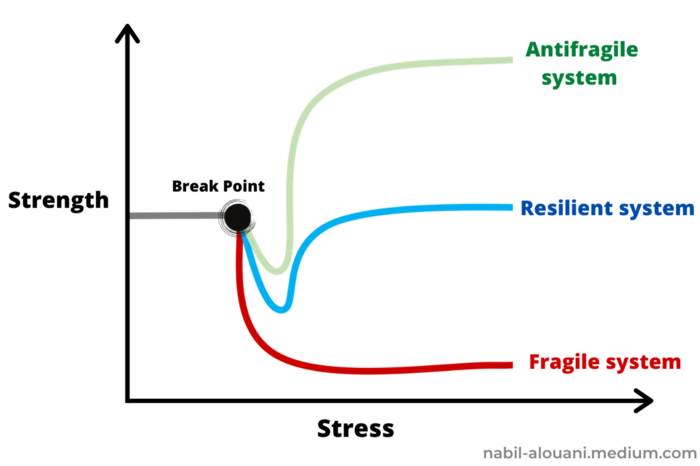
Time-changed things are antifragile. Culture, tech innovation, restaurants, revolutions, book sales, cuisine, economic success, and even muscle shape. These systems benefit from shocks and randomness in different ways, but they all pay a price for antifragility.
Same goes for the free market and financial institutions. Taleb's book uses restaurants as an example and ends with a reference to the 2008 crash.
“Restaurants are fragile. They compete with each other. But the collective of local restaurants is antifragile for that very reason. Had restaurants been individually robust, hence immortal, the overall business would be either stagnant or weak and would deliver nothing better than cafeteria food — and I mean Soviet-style cafeteria food. Further, it [the overall business] would be marred with systemic shortages, with once in a while a complete crisis and government bailout.”
Imagine the same thing with banks.
Independent banks would compete to offer the best services. If one of these banks fails, it will disappear. Customers and investors will suffer, but the market will recover from the dead banks' mistakes.
This idea underpins a free market. Bitcoin and other cryptocurrencies say this when criticizing traditional banking.
The traditional banking system's components never die. When a bank fails, the Federal Reserve steps in with a big taxpayer-funded check. This hinders bank evolution. If you don't let banking cells die and be replaced, your financial system won't be antifragile.
The interdependence of banks (centralization) means that one bank's mistake can sink the entire fleet, which brings us to SBF's ultimate travesty with FTX.
FTX has left the cryptocurrency gene pool.
FTX should be decentralized and independent. The super-star scammer invested in more than 130 crypto companies and linked them, creating a fragile banking-like structure. FTX seemed to say, "We exist because centralized banks are bad." But we'll be good, unlike the centralized banking system.
FTX saved several companies, including BlockFi and Voyager Digital.
FTX wanted to be a crypto bank conglomerate and Federal Reserve. SBF wanted to monopolize crypto markets. FTX wanted to be in bed with as many powerful people as possible, so SBF seduced politicians and celebrities.
Worst? People who saw SBF's plan flaws praised him. Experts, newspapers, and crypto fans praised FTX. When billions pour in, it's hard to realize FTX was acting against its nature.
Then, they act shocked when they realize FTX's fall triggered a domino effect. Some say the damage could wipe out the crypto market, but that's wrong.
Cell death is different from body death.
FTX is out of the game despite its size. Unfit, it fell victim to market natural selection.
Next?
The challengers keep coming. The crypto economy will improve with each failure.
Free markets are antifragile because their fragile parts compete, fostering evolution. With constructive feedback, evolution benefits customers and investors.
FTX shows that customers don't like being scammed, so the crypto market's health depends on them. Charlatans and con artists are eliminated quickly or slowly.
Crypto isn't immune to collapse. Cryptocurrencies can go extinct like biological species. Antifragility isn't immortality. A few more decades of evolution may be enough for humans to figure out how to best handle money, whether it's bitcoin, traditional banking, gold, or something else.
Keep your BS detector on. Start by being skeptical of this article's finance-related claims. Even if you think you understand finance, join the conversation.
We build a better future through dialogue. So listen, ask, and share. When you think you can't find common ground with the opposing view, remember:
Sam Bankman-Fried lied.

Chris
2 years ago
What the World's Most Intelligent Investor Recently Said About Crypto
Cryptoshit. This thing is crazy to buy.

Charlie Munger is revered and powerful in finance.
Munger, vice chairman of Berkshire Hathaway, is noted for his wit, no-nonsense attitude to investment, and ability to spot promising firms and markets.
Munger's crypto views have upset some despite his reputation as a straight shooter.
“There’s only one correct answer for intelligent people, just totally avoid all the people that are promoting it.” — Charlie Munger
The Munger Interview on CNBC (4:48 secs)
This Monday, CNBC co-anchor Rebecca Quick interviewed Munger and brought up his 2007 statement, "I'm not allowed to have an opinion on this subject until I can present the arguments against my viewpoint better than the folks who are supporting it."
Great investing and life advice!
If you can't explain the opposing reasons, you're not informed enough to have an opinion.
In today's world, it's important to grasp both sides of a debate before supporting one.
Rebecca inquired:
Does your Wall Street Journal article on banning cryptocurrency apply? If so, would you like to present the counterarguments?
Mungers reply:
I don't see any viable counterarguments. I think my opponents are idiots, hence there is no sensible argument against my position.
Consider his words.
Do you believe Munger has studied both sides?
He said, "I assume my opponents are idiots, thus there is no sensible argument against my position."
This is worrisome, especially from a guy who once encouraged studying both sides before forming an opinion.
Munger said:
National currencies have benefitted humanity more than almost anything else.
Hang on, I think we located the perpetrator.
Munger thinks crypto will replace currencies.
False.
I doubt he studied cryptocurrencies because the name is deceptive.
He misread a headline as a Dollar destroyer.
Cryptocurrencies are speculations.
Like Tesla, Amazon, Apple, Google, Microsoft, etc.
Crypto won't replace dollars.
In the interview with CNBC, Munger continued:
“I’m not proud of my country for allowing this crap, what I call the cryptoshit. It’s worthless, it’s no good, it’s crazy, it’ll do nothing but harm, it’s anti-social to allow it.” — Charlie Munger
Not entirely inaccurate.
Daily cryptos are established solely to pump and dump regular investors.
Let's get into Munger's crypto aversion.
Rat poison is bitcoin.
Munger famously dubbed Bitcoin rat poison and a speculative bubble that would implode.
Partially.
But the bubble broke. Since 2021, the market has fallen.
Scam currencies and NFTs are being eliminated, which I like.
Whoa.
Why does Munger doubt crypto?
Mungers thinks cryptocurrencies has no intrinsic value.
He worries about crypto fraud and money laundering.
Both are valid issues.
Yet grouping crypto is intellectually dishonest.
Ethereum, Bitcoin, Solana, Chainlink, Flow, and Dogecoin have different purposes and values (not saying they’re all good investments).
Fraudsters who hurt innocents will be punished.
Therefore, complaining is useless.
Why not stop it? Repair rather than complain.
Regrettably, individuals today don't offer solutions.
Blind Areas for Mungers
As with everyone, Mungers' bitcoin views may be impacted by his biases and experiences.
OK.
But Munger has always advocated classic value investing and may be wary of investing in an asset outside his expertise.
Mungers' banking and insurance investments may influence his bitcoin views.
Could a coworker or acquaintance have told him crypto is bad and goes against traditional finance?
Right?
Takeaways
Do you respect Charlie Mungers?
Yes and no, like any investor or individual.
To understand Mungers' bitcoin beliefs, you must be critical.
Mungers is a successful investor, but his views about bitcoin should be considered alongside other viewpoints.
Munger’s success as an investor has made him an influencer in the space.
Influence gives power.
He controls people's thoughts.
Munger's ok. He will always be heard.
I'll do so cautiously.
:max_bytes(150000):strip_icc():gifv():format(webp)/reiff_headshot-5bfc2a60c9e77c00519a70bd.jpg)
Nathan Reiff
3 years ago
Howey Test and Cryptocurrencies: 'Every ICO Is a Security'
What Is the Howey Test?
To determine whether a transaction qualifies as a "investment contract" and thus qualifies as a security, the Howey Test refers to the U.S. Supreme Court cass: the Securities Act of 1933 and the Securities Exchange Act of 1934. According to the Howey Test, an investment contract exists when "money is invested in a common enterprise with a reasonable expectation of profits from others' efforts."
The test applies to any contract, scheme, or transaction. The Howey Test helps investors and project backers understand blockchain and digital currency projects. ICOs and certain cryptocurrencies may be found to be "investment contracts" under the test.
Understanding the Howey Test
The Howey Test comes from the 1946 Supreme Court case SEC v. W.J. Howey Co. The Howey Company sold citrus groves to Florida buyers who leased them back to Howey. The company would maintain the groves and sell the fruit for the owners. Both parties benefited. Most buyers had no farming experience and were not required to farm the land.
The SEC intervened because Howey failed to register the transactions. The court ruled that the leaseback agreements were investment contracts.
This established four criteria for determining an investment contract. Investing contract:
- An investment of money
- n a common enterprise
- With the expectation of profit
- To be derived from the efforts of others
In the case of Howey, the buyers saw the transactions as valuable because others provided the labor and expertise. An income stream was obtained by only investing capital. As a result of the Howey Test, the transaction had to be registered with the SEC.
Howey Test and Cryptocurrencies
Bitcoin is notoriously difficult to categorize. Decentralized, they evade regulation in many ways. Regardless, the SEC is looking into digital assets and determining when their sale qualifies as an investment contract.
The SEC claims that selling digital assets meets the "investment of money" test because fiat money or other digital assets are being exchanged. Like the "common enterprise" test.
Whether a digital asset qualifies as an investment contract depends on whether there is a "expectation of profit from others' efforts."
For example, buyers of digital assets may be relying on others' efforts if they expect the project's backers to build and maintain the digital network, rather than a dispersed community of unaffiliated users. Also, if the project's backers create scarcity by burning tokens, the test is met. Another way the "efforts of others" test is met is if the project's backers continue to act in a managerial role.
These are just a few examples given by the SEC. If a project's success is dependent on ongoing support from backers, the buyer of the digital asset is likely relying on "others' efforts."
Special Considerations
If the SEC determines a cryptocurrency token is a security, many issues arise. It means the SEC can decide whether a token can be sold to US investors and forces the project to register.
In 2017, the SEC ruled that selling DAO tokens for Ether violated federal securities laws. Instead of enforcing securities laws, the SEC issued a warning to the cryptocurrency industry.
Due to the Howey Test, most ICOs today are likely inaccessible to US investors. After a year of ICOs, then-SEC Chair Jay Clayton declared them all securities.
SEC Chairman Gensler Agrees With Predecessor: 'Every ICO Is a Security'
Howey Test FAQs
How Do You Determine If Something Is a Security?
The Howey Test determines whether certain transactions are "investment contracts." Securities are transactions that qualify as "investment contracts" under the Securities Act of 1933 and the Securities Exchange Act of 1934.
The Howey Test looks for a "investment of money in a common enterprise with a reasonable expectation of profits from others' efforts." If so, the Securities Act of 1933 and the Securities Exchange Act of 1934 require disclosure and registration.
Why Is Bitcoin Not a Security?
Former SEC Chair Jay Clayton clarified in June 2018 that bitcoin is not a security: "Cryptocurrencies: Replace the dollar, euro, and yen with bitcoin. That type of currency is not a security," said Clayton.
Bitcoin, which has never sought public funding to develop its technology, fails the SEC's Howey Test. However, according to Clayton, ICO tokens are securities.
A Security Defined by the SEC
In the public and private markets, securities are fungible and tradeable financial instruments. The SEC regulates public securities sales.
The Supreme Court defined a security offering in SEC v. W.J. Howey Co. In its judgment, the court defines a security using four criteria:
- An investment contract's existence
- The formation of a common enterprise
- The issuer's profit promise
- Third-party promotion of the offering
Read original post.
You might also like

Simone Basso
3 years ago
How I set up my teams to be successful
After 10 years of working in scale-ups, I've embraced a few concepts for scaling Tech and Product teams.
First, cross-functionalize teams. Product Managers represent the business, Product Designers the consumer, and Engineers build.
I organize teams of 5-10 individuals, following AWS's two pizza teams guidelines, with a Product Trio guiding each.
If more individuals are needed to reach a goal, I group teams under a Product Trio.
With Engineering being the biggest group, Staff/Principal Engineers often support the Trio on cross-team technical decisions.
Product Managers, Engineering Managers, or Engineers in the team may manage projects (depending on the project or aim), but the trio is collectively responsible for the team's output and outcome.
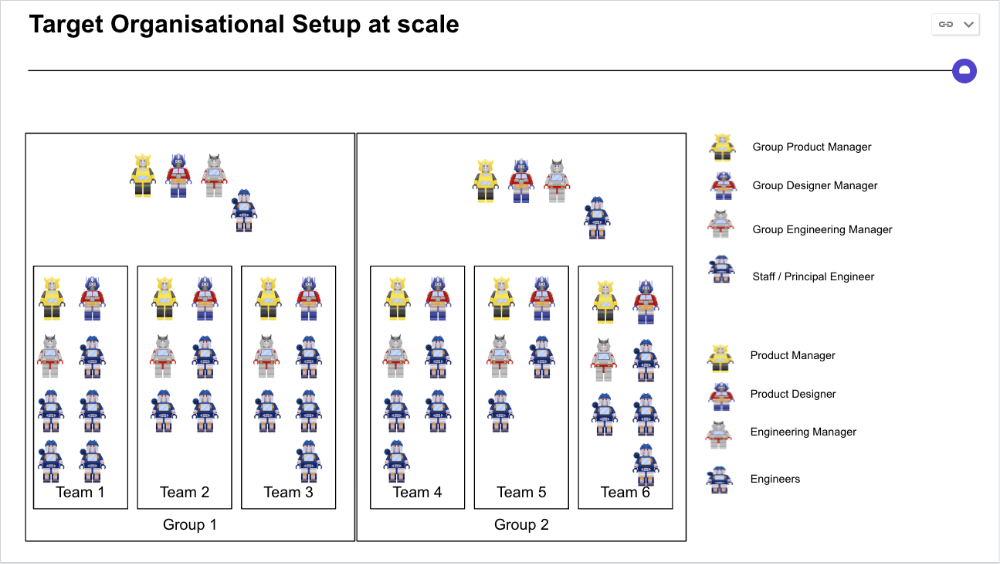
Once the Product Trio model is created, roles, duties, team ceremonies, and cooperation models must be clarified.
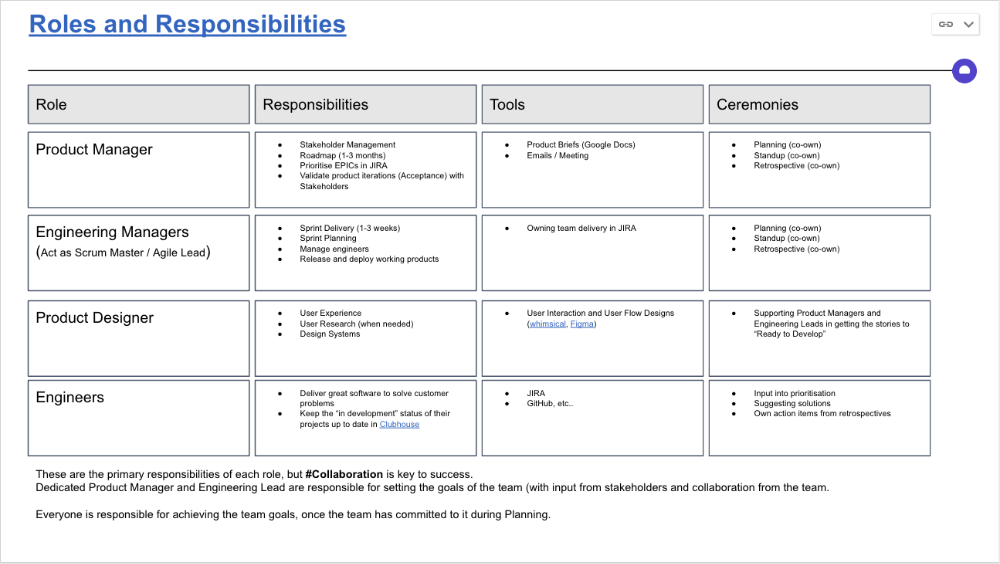
Keep reporting lines by discipline. Line managers are accountable for each individual's advancement, thus it's crucial that they know the work in detail.

Cross-team collaboration becomes more important after 3 teams (15-30 people). Teams can easily diverge in how they write code, run ceremonies, and build products.
Establishing groups of people that are cross-team, but grouped by discipline and skills, sharing and agreeing on working practices becomes critical.
The “Spotify Guild” model has been where I’ve taken a lot of my inspiration from.
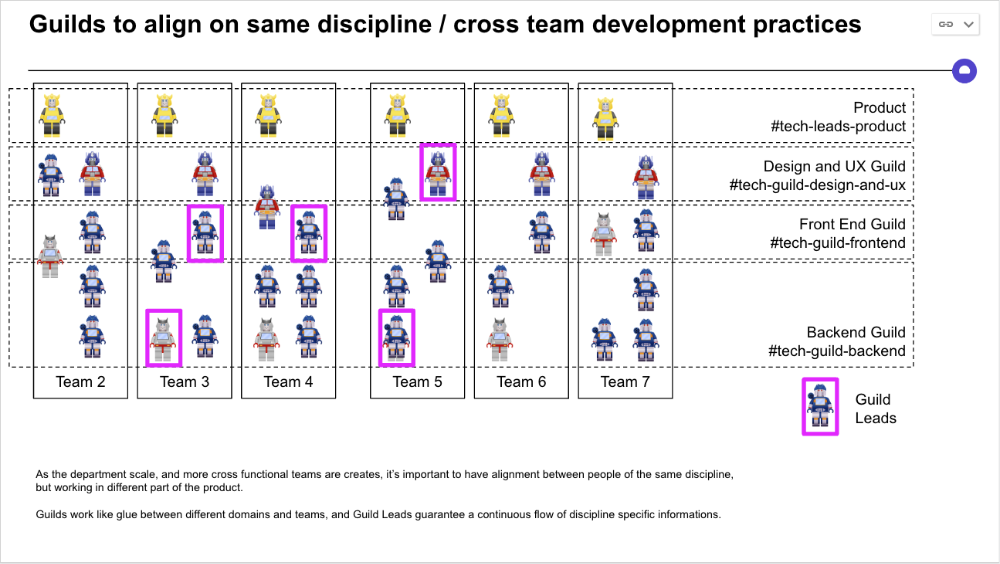
Last, establish a taxonomy for communication channels.
In Slack, I create one channel per team and one per guild (and one for me to have discussions with the team leads).
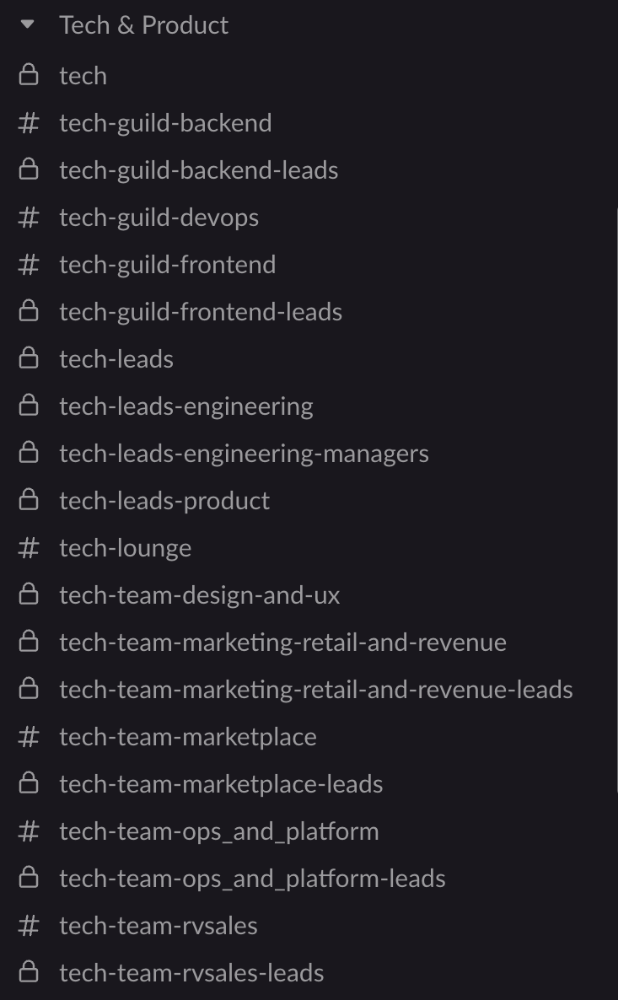
These are just some of the basic principles I follow to organize teams.
A book I particularly like about team types and how they interact with each other is https://teamtopologies.com/.

Jon Brosio
3 years ago
You can learn more about marketing from these 8 copywriting frameworks than from a college education.
Email, landing pages, and digital content

Today's most significant skill:
Copywriting.
Unfortunately, most people don't know how to write successful copy because they weren't taught in school.
I've been obsessed with copywriting for two years. I've read 15 books, completed 3 courses, and studied internet's best digital entrepreneurs.
Here are 8 copywriting frameworks that educate more than a four-year degree.
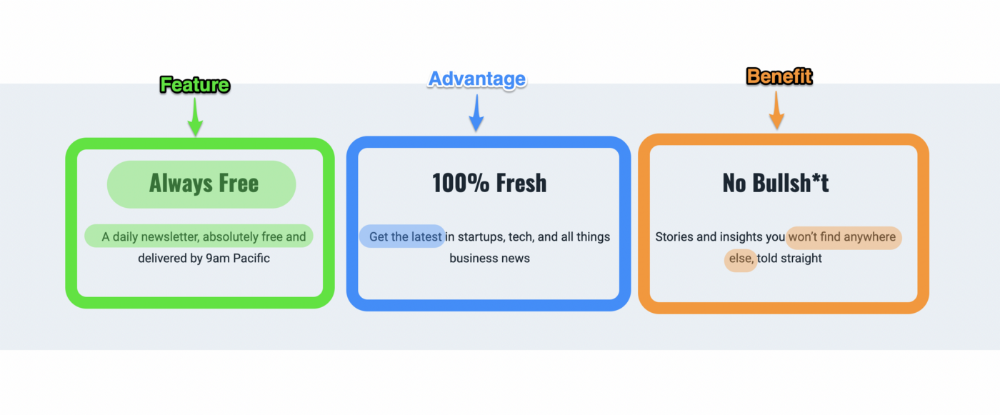
1. Feature — Advantage — Benefit (F.A.B)
This is the most basic copywriting foundation. Email marketing, landing page copy, and digital video ads can use it.
F.A.B says:
How it works (feature)
which is helpful (advantage)
What's at stake (benefit)
The Hustle uses this framework on their landing page to convince people to sign up:
2. P. A. S. T. O. R.
This framework is for longer-form copywriting. PASTOR uses stories to engage with prospects. It explains why people should buy this offer.
PASTOR means:
Problem
Amplify
Story
Testimonial
Offer
Response
Dan Koe's landing page is a great example. It shows PASTOR frame-by-frame.

3. Before — After — Bridge
Before-after-bridge is a copywriting framework that draws attention and shows value quickly.
This framework highlights:
where you are
where you want to be
how to get there
Works great for: Email threads/landing pages
Zain Kahn utilizes this framework to write viral threads.

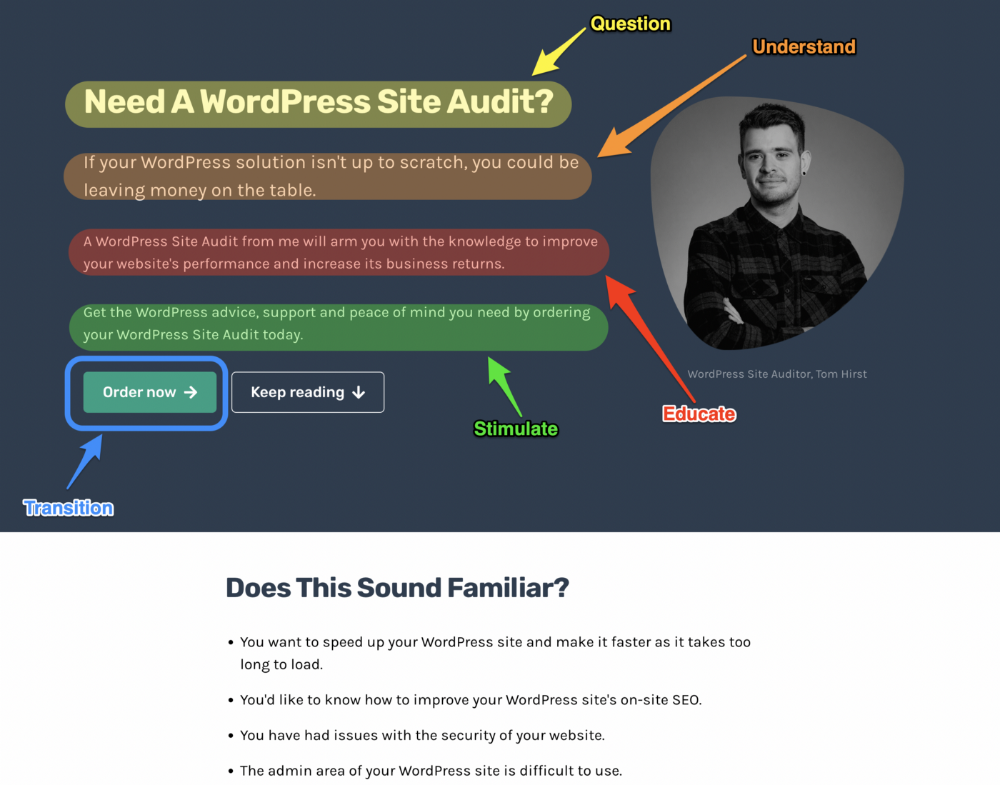
4. Q.U.E.S.T
QUEST is about empathetic writing. You know their issues, obstacles, and headaches. This allows coverups.
QUEST:
Qualifies
Understands
Educates
Stimulates
Transitions
Tom Hirst's landing page uses the QUEST framework.
5. The 4P’s model
The 4P’s approach pushes your prospect to action. It educates and persuades quickly.
4Ps:
The problem the visitor is dealing with
The promise that will help them
The proof the promise works
A push towards action
Mark Manson is a bestselling author, digital creator, and pop-philosopher. He's also a great copywriter, and his membership offer uses the 4P’s framework.

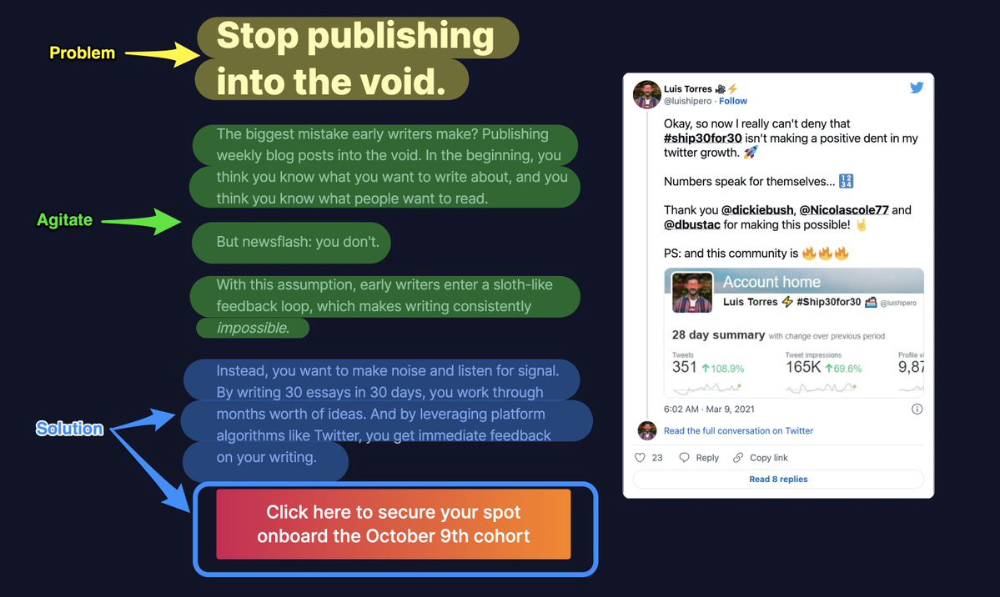
6. Problem — Agitate — Solution (P.A.S)
Up-and-coming marketers should understand problem-agitate-solution copywriting. Once you understand one structure, others are easier. It drives passion and presents a clear solution.
PAS outlines:
The issue the visitor is having
It then intensifies this issue through emotion.
finally offers an answer to that issue (the offer)
The customer's story loops. Nicolas Cole and Dickie Bush use PAS to promote Ship 30 for 30.
7. Star — Story — Solution (S.S.S)
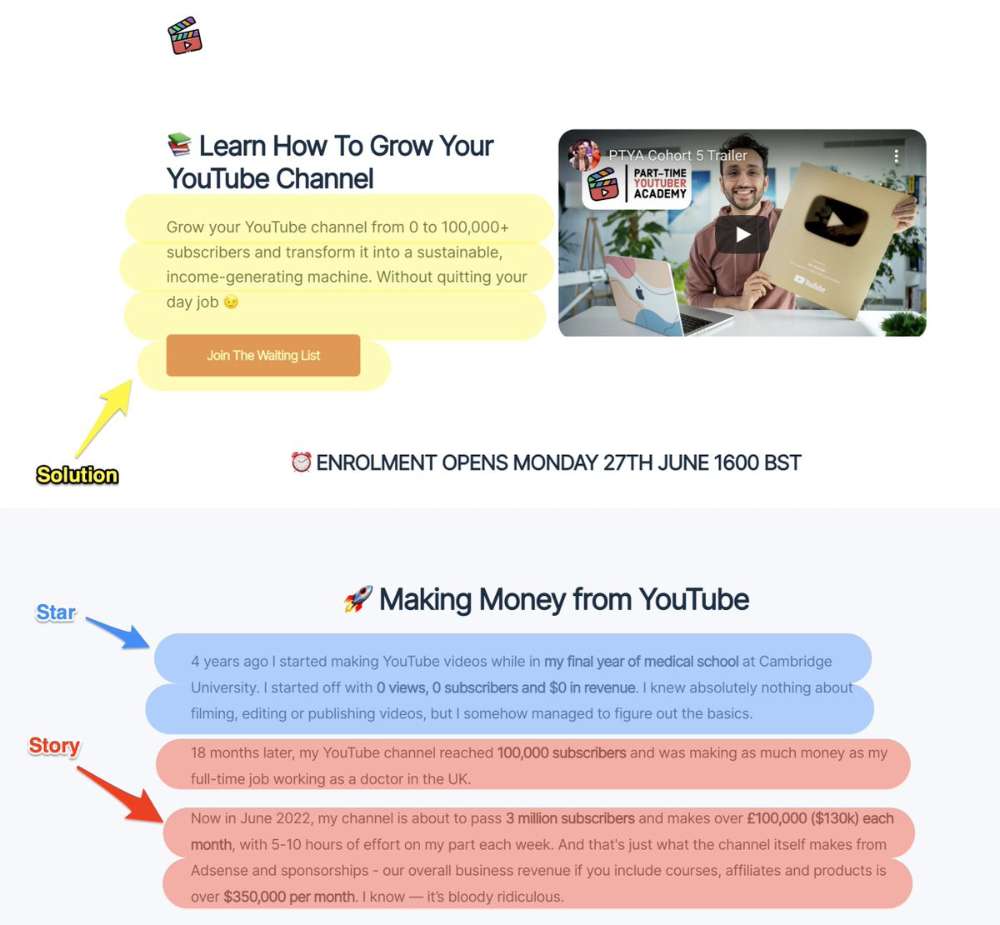
PASTOR + PAS = star-solution-story. Like PAS, it employs stories to persuade.
S.S.S. is effective storytelling:
Star: (Person had a problem)
Story: (until they had a breakthrough)
Solution: (That created a transformation)
Ali Abdaal is a YouTuber with a great S.S.S copy.
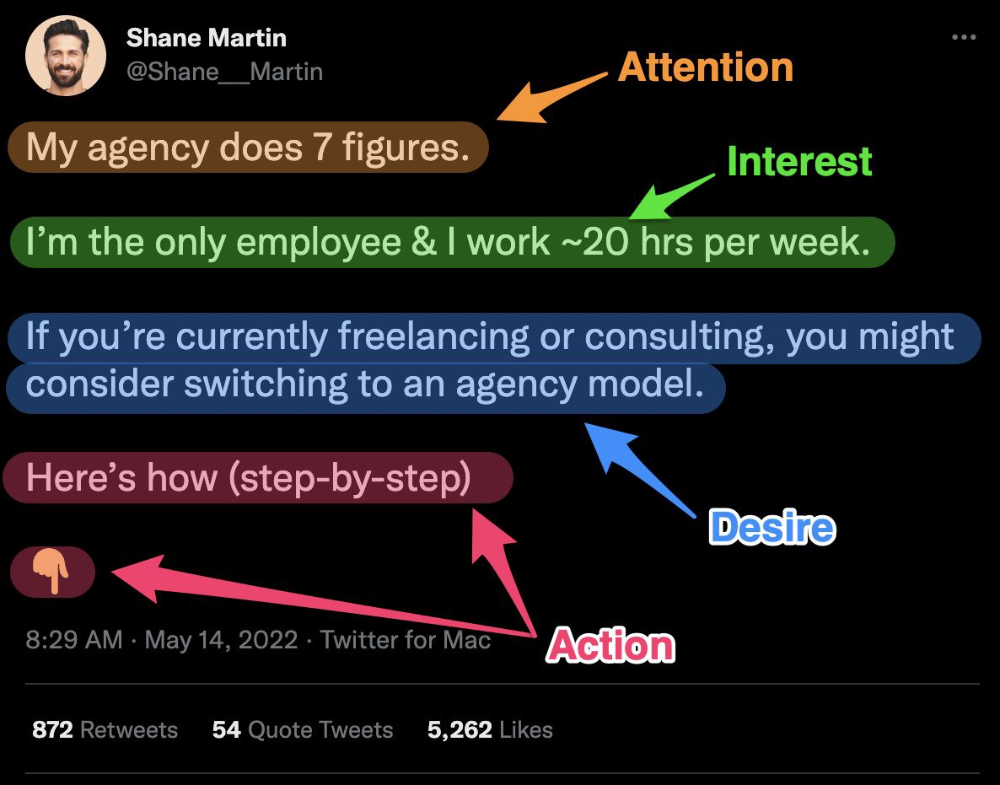
8. Attention — Interest — Desire — Action
AIDA is another classic. This copywriting framework is great for fast-paced environments (think all digital content on Linkedin, Twitter, Medium, etc.).
It works with:
Page landings
writing on thread
Email
It's a good structure since it's concise, attention-grabbing, and action-oriented.
Shane Martin, Twitter's creator, uses this approach to create viral content.
TL;DR
8 copywriting frameworks that teach marketing better than a four-year degree
Feature-advantage-benefit
Before-after-bridge
Star-story-solution
P.A.S.T.O.R
Q.U.E.S.T
A.I.D.A
P.A.S
4P’s

Matthew O'Riordan
3 years ago
Trends in SaaS Funding from 2016 to 2022
Christopher Janz of Point Nine Capital created the SaaS napkin in 2016. This post shows how founders have raised cash in the last 6 years. View raw data.
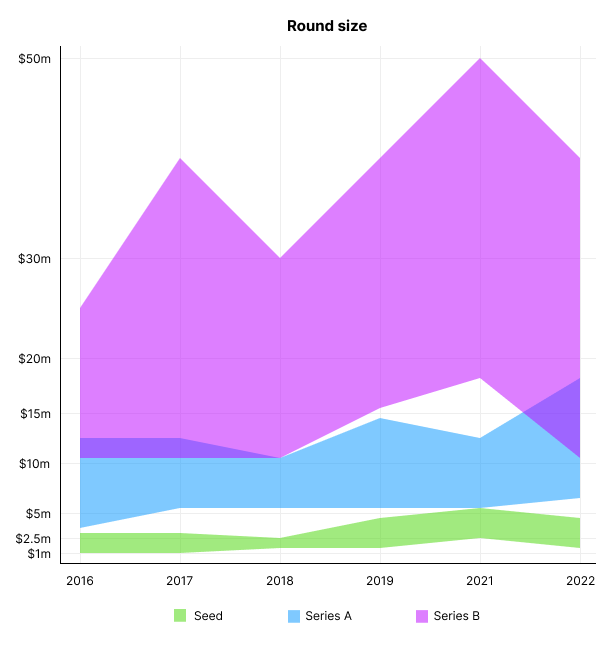
Round size
Unsurprisingly, round sizes have expanded and will taper down in 2022. In 2016, pre-seed rounds were $200k to $500k; currently, they're $1-$2m. Despite the macroeconomic scenario, Series A have expanded from $3m to $12m in 2016 to $6m and $18m in 2022.
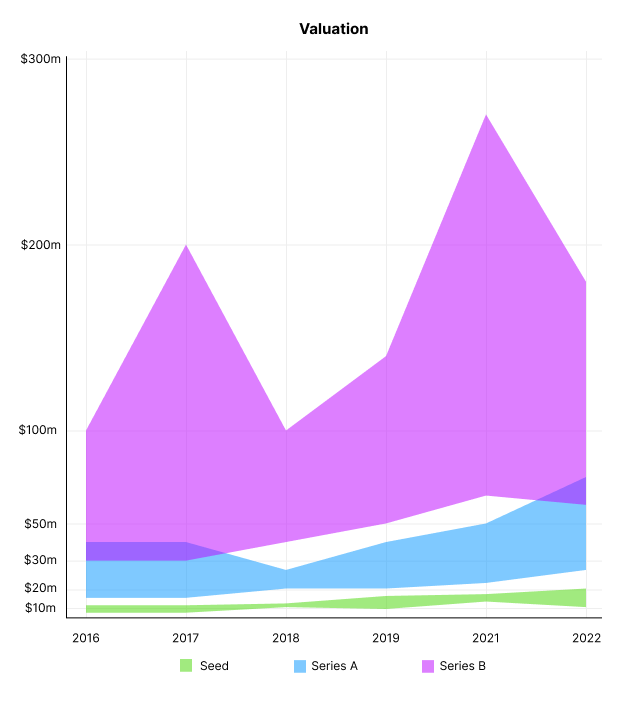
Valuation
There are hints that valuations are rebounding this year. Pre-seed valuations in 2022 are $12m from $3m in 2016, and Series B prices are $270m from $100m in 2016.
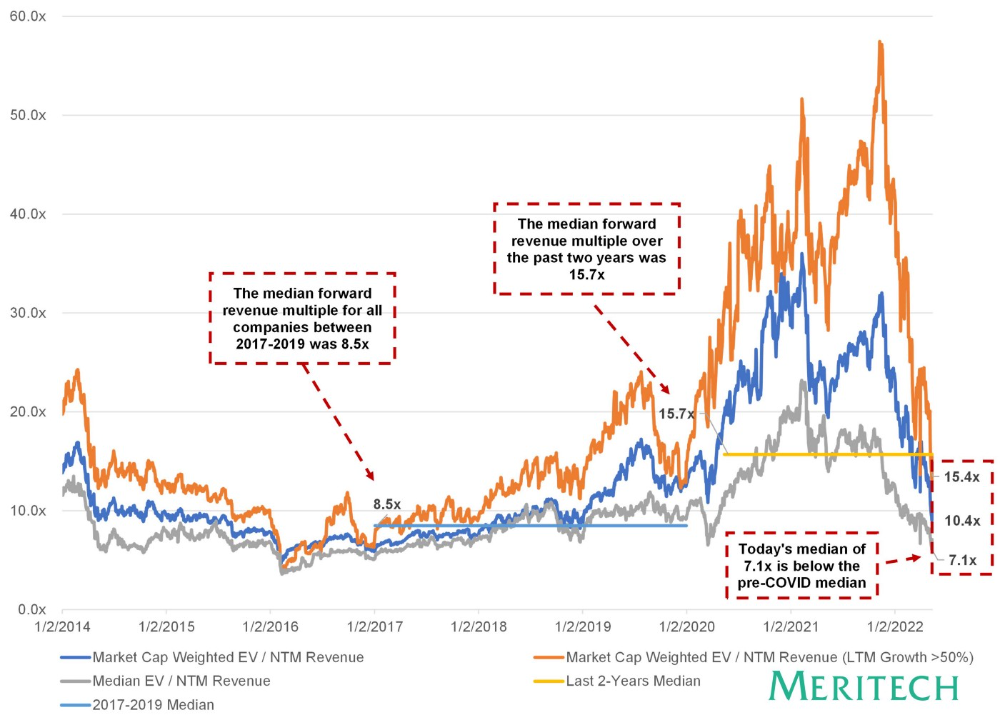
Compared to public SaaS multiples, Series B valuations more closely reflect the market, but Seed and Series A prices seem to be inflated regardless of the market.
I'd like to know how each annual cohort performed for investors, based on the year they invested and the valuations. I can't access this information.
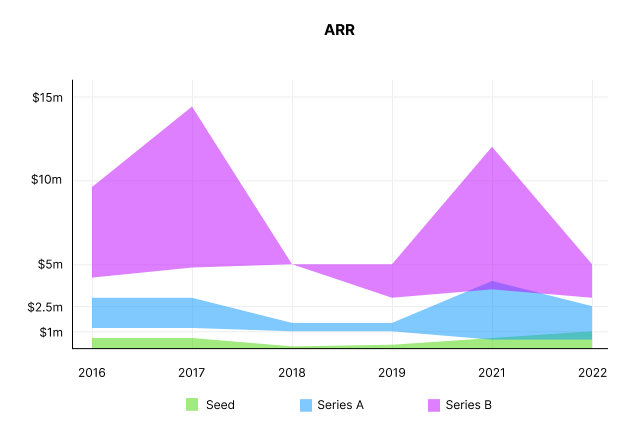
ARR
Seed firms' ARR forecasts have risen from $0 to $0.6m to $0 to $1m. 2016 expected $1.2m to $3m, 2021 $0.5m to $4m, and this year $0.5m to $2.5m, suggesting that Series A firms may raise with less ARR today. Series B minutes fell from $4.2m to $3m.
Capitalization Rate
2022 is the year that VCs start discussing capital efficiency in portfolio meetings. Given the economic shift in the markets and the stealthy VC meltdown, it's not surprising. Christopher Janz added capital efficiency to the SaaS Napkin as a new statistic for Series A (3.5x) and Series B. (2.5x). Your investors must live under a rock if they haven't asked about capital efficiency. If you're unsure:
The Capital Efficiency Ratio is the ratio of how much a company has spent growing revenue and how much they’re receiving in return. It is the broadest measure of company effectiveness in generating ARR
What next?
No one knows what's next, including me. All startup and growing enterprises around me are tightening their belts and extending their runways in anticipation of a difficult fundraising ride. If you're wanting to raise money but can wait, wait till the market is more stable and access to money is easier.
