More on Web3 & Crypto

Trent Lapinski
4 years ago
What The Hell Is A Crypto Punk?
We are Crypto Punks, and we are changing your world.
A “Crypto Punk” is a new generation of entrepreneurs who value individual liberty and collective value creation and co-creation through decentralization. While many Crypto Punks were born and raised in a digital world, some of the early pioneers in the crypto space are from the Oregon Trail generation. They were born to an analog world, but grew up simultaneously alongside the birth of home computing, the Internet, and mobile computing.
A Crypto Punk’s world view is not the same as previous generations. By the time most Crypto Punks were born everything from fiat currency, the stock market, pharmaceuticals, the Internet, to advanced operating systems and microprocessing were already present or emerging. Crypto Punks were born into pre-existing conditions and systems of control, not governed by logic or reason but by greed, corporatism, subversion, bureaucracy, censorship, and inefficiency.
All Systems Are Human Made
Crypto Punks understand that all systems were created by people and that previous generations did not have access to information technologies that we have today. This is why Crypto Punks have different values than their parents, and value liberty, decentralization, equality, social justice, and freedom over wealth, money, and power. They understand that the only path forward is to work together to build new and better systems that make the old world order obsolete.
Unlike the original cypher punks and cyber punks, Crypto Punks are a new iteration or evolution of these previous cultures influenced by cryptography, blockchain technology, crypto economics, libertarianism, holographics, democratic socialism, and artificial intelligence. They are tasked with not only undoing the mistakes of previous generations, but also innovating and creating new ways of solving complex problems with advanced technology and solutions.
Where Crypto Punks truly differ is in their understanding that computer systems can exist for more than just engagement and entertainment, but actually improve the human condition by automating bureaucracy and inefficiency by creating more efficient economic incentives and systems.
Crypto Punks Value Transparency and Do Not Trust Flawed, Unequal, and Corrupt Systems
Crypto Punks have a strong distrust for inherently flawed and corrupt systems. This why Crypto Punks value transparency, free speech, privacy, and decentralization. As well as arguably computer systems over human powered systems.
Crypto Punks are the children of the Great Recession, and will never forget the economic corruption that still enslaves younger generations.
Crypto Punks were born to think different, and raised by computers to view reality through an LED looking glass. They will not surrender to the flawed systems of economic wage slavery, inequality, censorship, and subjection. They will literally engineer their own unstoppable financial systems and trade in cryptography over fiat currency merely to prove that belief systems are more powerful than corruption.
Crypto Punks are here to help achieve freedom from world governments, corporations and bankers who monetizine our data to control our lives.
Crypto Punks Decentralize
Despite all the evils of the world today, Crypto Punks know they have the power to create change. This is why Crypto Punks are optimistic about the future despite all the indicators that humanity is destined for failure.
Crypto Punks believe in systems that prioritize people and the planet above profit. Even so, Crypto Punks still believe in capitalistic systems, but only capitalistic systems that incentivize good behaviors that do not violate the common good for the sake of profit.
Cyber Punks Are Co-Creators
We are Crypto Punks, and we will build a better world for all of us. For the true price of creation is not in US dollars, but through working together as equals to replace the unequal and corrupt greedy systems of previous generations.
Where they have failed, Crypto Punks will succeed. Not because we want to, but because we have to. The world we were born into is so corrupt and its systems so flawed and unequal we were never given a choice.
We have to be the change we seek.
We are Crypto Punks.
Either help us, or get out of our way.
Are you a Crypto Punk?
Alex Bentley
3 years ago
Why Bill Gates thinks Bitcoin, crypto, and NFTs are foolish
Microsoft co-founder Bill Gates assesses digital assets while the bull is caged.

Bill Gates is well-respected.
Reasonably. He co-founded and led Microsoft during its 1980s and 1990s revolution.
After leaving Microsoft, Bill Gates pursued other interests. He and his wife founded one of the world's largest philanthropic organizations, Bill & Melinda Gates Foundation. He also supports immunizations, population control, and other global health programs.
When Gates criticized Bitcoin, cryptocurrencies, and NFTs, it made news.
Bill Gates said at the 58th Munich Security Conference...
“You have an asset class that’s 100% based on some sort of greater fool theory that somebody’s going to pay more for it than I do.”
Gates means digital assets. Like many bitcoin critics, he says digital coins and tokens are speculative.
And he's not alone. Financial experts have dubbed Bitcoin and other digital assets a "bubble" for a decade.
Gates also made fun of Bored Ape Yacht Club and NFTs, saying, "Obviously pricey digital photographs of monkeys will help the world."
Why does Bill Gates dislike digital assets?
According to Gates' latest comments, Bitcoin, cryptos, and NFTs aren't good ways to hold value.
Bill Gates is a better investor than Elon Musk.
“I’m used to asset classes, like a farm where they have output, or like a company where they make products,” Gates said.
The Guardian claimed in April 2021 that Bill and Melinda Gates owned the most U.S. farms. Over 242,000 acres of farmland.
The Gates couple has enough farmland to cover Hong Kong.

Bill Gates is a classic investor. He wants companies with an excellent track record, strong fundamentals, and good management. Or tangible assets like land and property.
Gates prefers the "old economy" over the "new economy"
Gates' criticism of Bitcoin and cryptocurrency ventures isn't surprising. These digital assets lack all of Gates's investing criteria.
Volatile digital assets include Bitcoin. Their costs might change dramatically in a day. Volatility scares risk-averse investors like Gates.
Gates has a stake in the old financial system. As Microsoft's co-founder, Gates helped develop a dominant tech company.
Because of his business, he's one of the world's richest men.
Bill Gates is invested in protecting the current paradigm.
He won't invest in anything that could destroy the global economy.
When Gates criticizes Bitcoin, cryptocurrencies, and NFTs, he's suggesting they're a hoax. These soapbox speeches are one way he protects his interests.
Digital assets aren't a bad investment, though. Many think they're the future.
Changpeng Zhao and Brian Armstrong are two digital asset billionaires. Two crypto exchange CEOs. Binance/Coinbase.
Digital asset revolution won't end soon.
If you disagree with Bill Gates and plan to invest in Bitcoin, cryptocurrencies, or NFTs, do your own research and understand the risks.
But don’t take Bill Gates’ word for it.
He’s just an old rich guy with a lot of farmland.
He has a lot to lose if Bitcoin and other digital assets gain global popularity.
This post is a summary. Read the full article here.

Crypto Zen Monk
2 years ago
How to DYOR in the world of cryptocurrency
RESEARCH
We must create separate ideas and handle our own risks to be better investors. DYOR is crucial.
The only thing unsustainable is your cluelessness.
DYOR: Why
On social media, there is a lot of false information and divergent viewpoints. All of these facts might be accurate, but they might not be appropriate for your portfolio and investment preferences.
You become a more knowledgeable investor thanks to DYOR.
DYOR improves your portfolio's risk management.
My DYOR resources are below.

Messari: Major Blockchains' Activities
New York-based Messari provides cryptocurrency open data libraries.
Major blockchains offer 24-hour on-chain volume. https://messari.io/screener/most-active-chains-DB01F96B
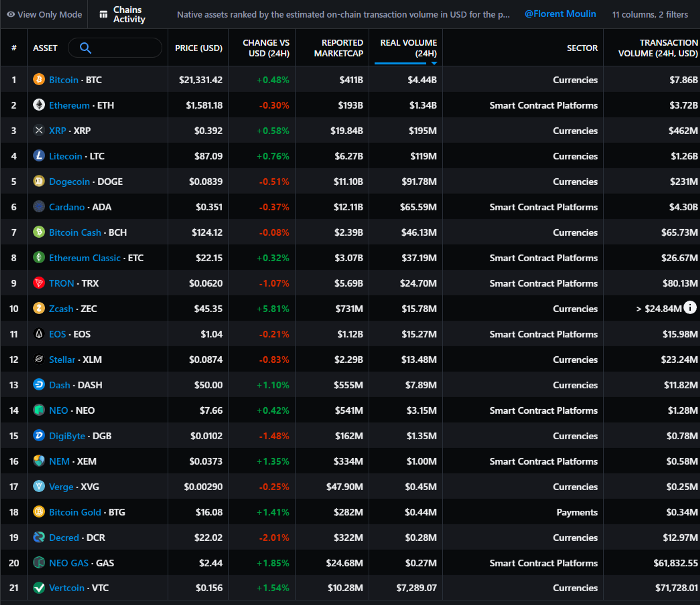
What to do
Invest in stable cryptocurrencies. Sort Messari by Real Volume (24H) or Reported Market Cap.
Coingecko: Research on Ecosystems
Top 10 Ecosystems by Coingecko are good.
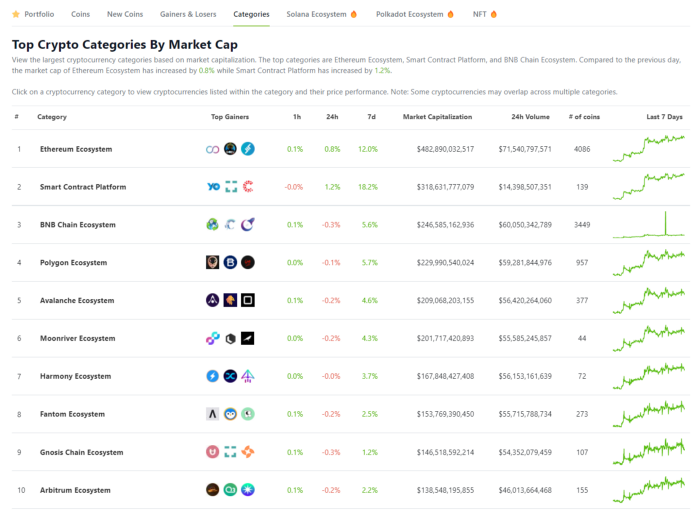
What to do
Invest in quality.
Leading ten Ecosystems by Market Cap
There are a lot of coins in the ecosystem (second last column of above chart)
CoinGecko's Market Cap Crypto Categories Market capitalization-based cryptocurrency categories. Ethereum Ecosystem www.coingecko.com
Fear & Greed Index for Bitcoin (FGI)
The Bitcoin market sentiment index ranges from 0 (extreme dread) to 100. (extreme greed).
How to Apply
See market sentiment:
Extreme fright = opportunity to buy
Extreme greed creates sales opportunity (market due for correction).
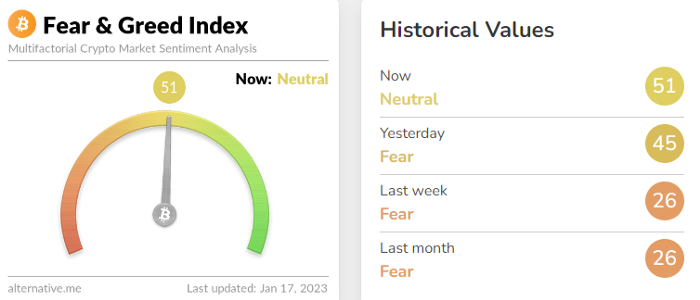
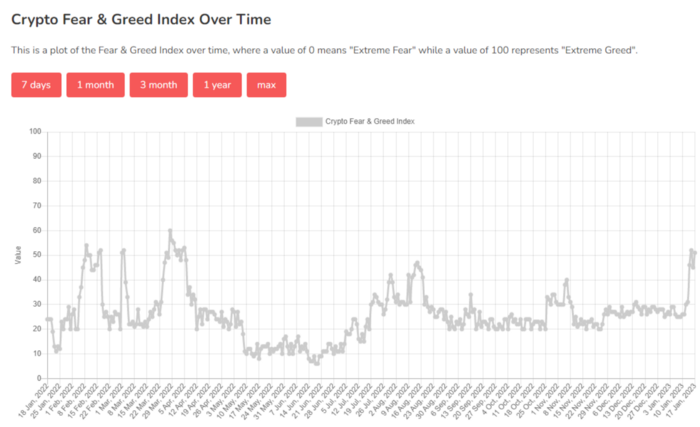
Glassnode
Glassnode gives facts, information, and confidence to make better Bitcoin, Ethereum, and cryptocurrency investments and trades.
Explore free and paid metrics.
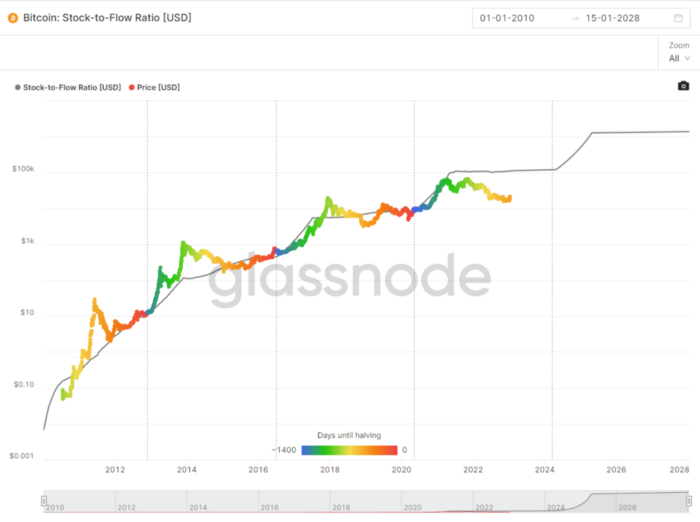
Stock to Flow Ratio: Application
The popular Stock to Flow Ratio concept believes scarcity drives value. Stock to flow is the ratio of circulating Bitcoin supply to fresh production (i.e. newly mined bitcoins). The S/F Ratio has historically predicted Bitcoin prices. PlanB invented this metric.
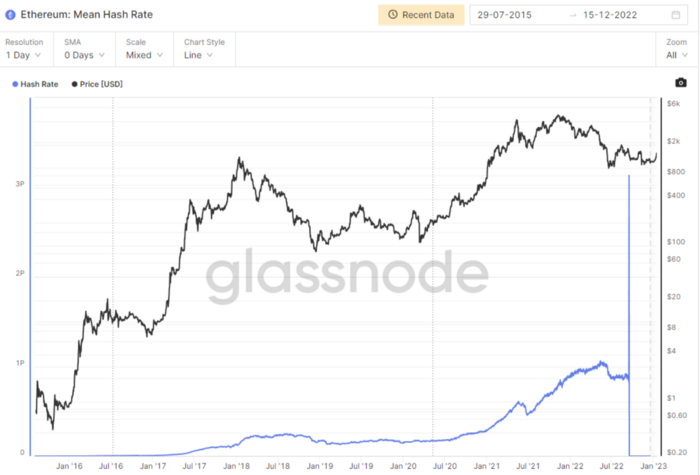
Utilization: Ethereum Hash Rate
Ethereum miners produce an estimated number of hashes per second.
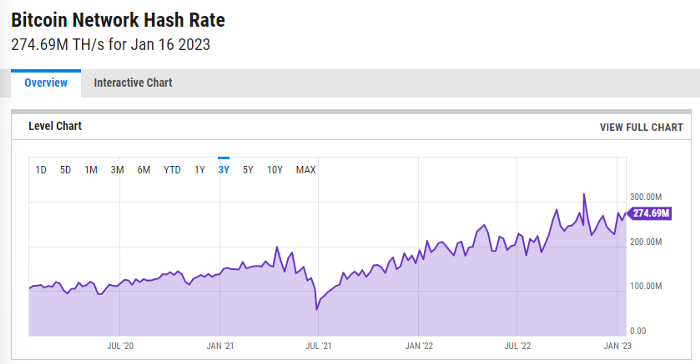
ycharts: Hash rate of the Bitcoin network
TradingView
TradingView is your go-to tool for investment analysis, watch lists, technical analysis, and recommendations from other traders/investors.
Research for a cryptocurrency project
Two key questions every successful project must ask: Q1: What is this project trying to solve? Is it a big problem or minor? Q2: How does this project make money?
Each cryptocurrency:
Check out the white paper.
check out the project's internet presence on github, twitter, and medium.
the transparency of it
Verify the team structure and founders. Verify their LinkedIn profile, academic history, and other qualifications. Search for their names with scam.
Where to purchase and use cryptocurrencies Is it traded on trustworthy exchanges?
From CoinGecko and CoinMarketCap, we may learn about market cap, circulations, and other important data.
The project must solve a problem. Solving a problem is the goal of the founders.
Avoid projects that resemble multi-level marketing or ponzi schemes.
Your use of social media
Use social media carefully or ignore it: Twitter, TradingView, and YouTube
Someone said this before and there are some truth to it. Social media bullish => short.
Your Behavior
Investigate. Spend time. You decide. Worth it!
Only you have the best interest in your financial future.
You might also like

SAHIL SAPRU
3 years ago
Growth tactics that grew businesses from 1 to 100
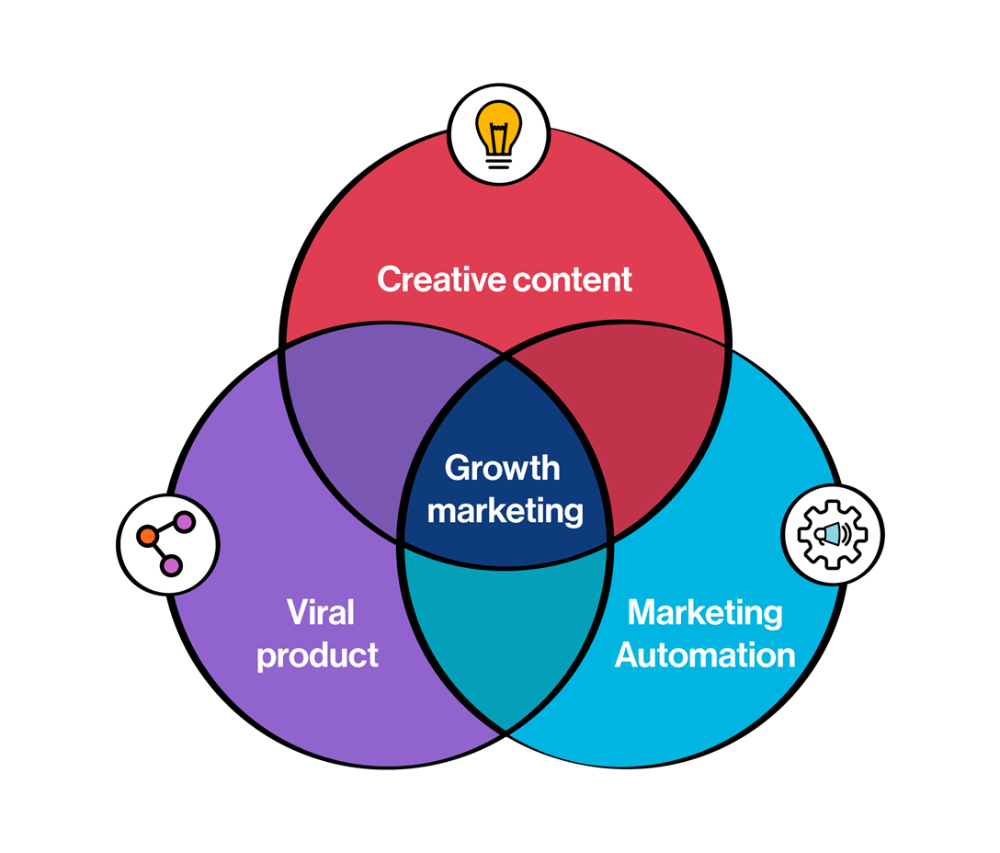
Everyone wants a scalable startup.
Innovation helps launch a startup. The secret to a scalable business is growth trials (from 1 to 100).
Growth marketing combines marketing and product development for long-term growth.
Today, I'll explain growth hacking strategies popular startups used to scale.
1/ A Facebook user's social value is proportional to their friends.
Facebook built its user base using content marketing and paid ads. Mark and his investors feared in 2007 when Facebook's growth stalled at 90 million users.
Chamath Palihapitiya was brought in by Mark.
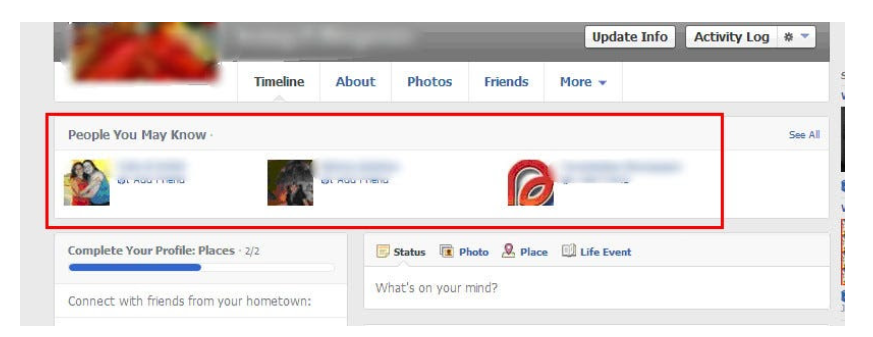
The team tested SEO keywords and MAU chasing. The growth team introduced “people you may know”
This feature reunited long-lost friends and family. Casual users became power users as the retention curve flattened.
Growth Hack Insights: With social network effect the value of your product or platform increases exponentially if you have users you know or can relate with.
2/ Airbnb - Focus on your value propositions
Airbnb nearly failed in 2009. The company's weekly revenue was $200 and they had less than 2 months of runway.
Enter Paul Graham. The team noticed a pattern in 40 listings. Their website's property photos sucked.
Why?
Because these photos were taken with regular smartphones. Users didn't like the first impression.
Graham suggested traveling to New York to rent a camera, meet with property owners, and replace amateur photos with high-resolution ones.
A week later, the team's weekly revenue doubled to $400, indicating they were on track.
Growth Hack Insights: When selling an “online experience” ensure that your value proposition is aesthetic enough for users to enjoy being associated with them.

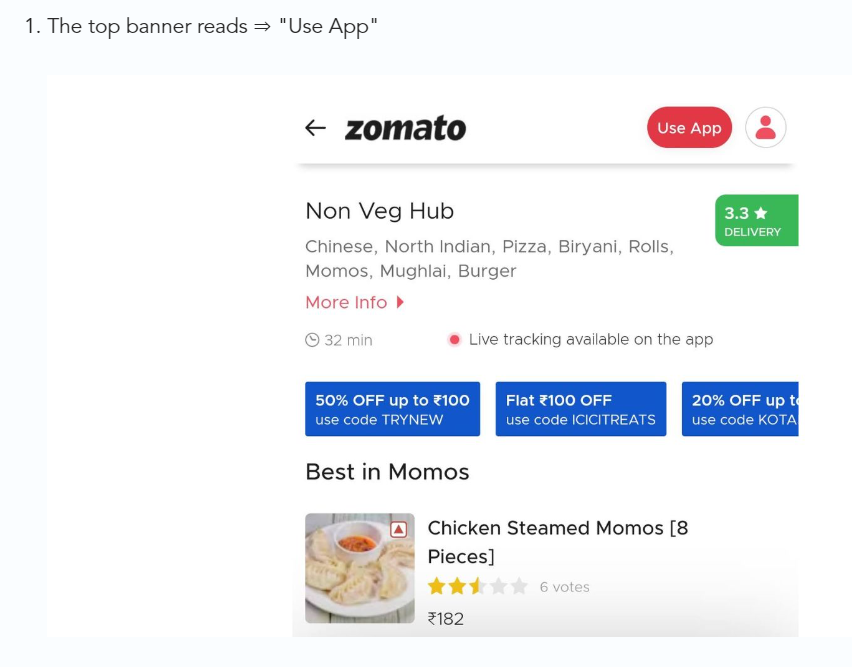
3/ Zomato - A company's smartphone push ensured growth.
Zomato delivers food. User retention was a challenge for the founders. Indian food customers are notorious for switching brands at the drop of a hat.
Zomato wanted users to order food online and repeat orders throughout the week.
Zomato created an attractive website with “near me” keywords for SEO indexing.
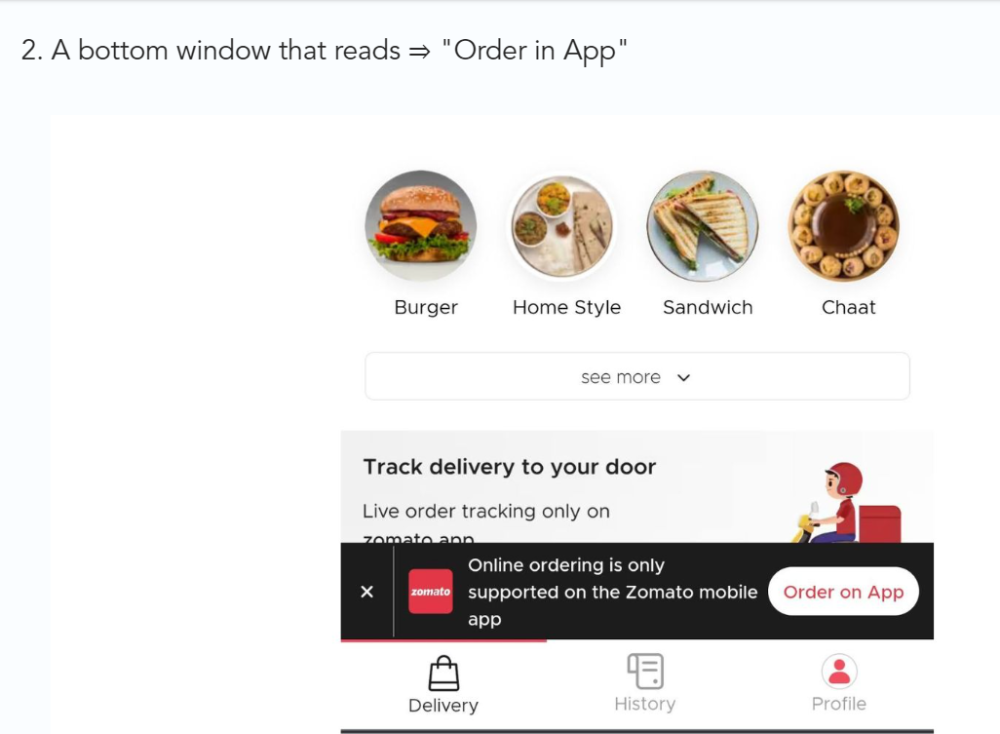
Zomato gambled to increase repeat orders. They only allowed mobile app food orders.
Zomato thought mobile apps were stickier. Product innovations in search/discovery/ordering or marketing campaigns like discounts/in-app notifications/nudges can improve user experience.
Zomato went public in 2021 after users kept ordering food online.
Growth Hack Insights: To improve user retention try to build platforms that build user stickiness. Your product and marketing team will do the rest for them.
4/ Hotmail - Signaling helps build premium users.
Ever sent or received an email or tweet with a sign — sent from iPhone?
Hotmail did it first! One investor suggested Hotmail add a signature to every email.
Overnight, thousands joined the company. Six months later, the company had 1 million users.
When serving an existing customer, improve their social standing. Signaling keeps the top 1%.
5/ Dropbox - Respect loyal customers
Dropbox is a company that puts people over profits. The company prioritized existing users.
Dropbox rewarded loyal users by offering 250 MB of free storage to anyone who referred a friend. The referral hack helped Dropbox get millions of downloads in its first few months.
Growth Hack Insights: Think of ways to improve the social positioning of your end-user when you are serving an existing customer. Signaling goes a long way in attracting the top 1% to stay.
These experiments weren’t hacks. Hundreds of failed experiments and user research drove these experiments. Scaling up experiments is difficult.
Contact me if you want to grow your startup's user base.

Startup Journal
3 years ago
The Top 14 Software Business Ideas That Are Sure To Succeed in 2023
Software can change any company.

Software is becoming essential. Everyone should consider how software affects their lives and others'.
Software on your phone, tablet, or computer offers many new options. We're experts in enough ways now.
Software Business Ideas will be popular by 2023.
ERP Programs
ERP software meets rising demand.
ERP solutions automate and monitor tasks that large organizations, businesses, and even schools would struggle to do manually.
ERP software could reach $49 billion by 2024.
CRM Program
CRM software is a must-have for any customer-focused business.
Having an open mind about your business services and products allows you to change platforms.
Another company may only want your CRM service.
Medical software
Healthcare facilities need reliable, easy-to-use software.
EHRs, MDDBs, E-Prescribing, and more are software options.
The global medical software market could reach $11 billion by 2025, and mobile medical apps may follow.
Presentation Software in the Cloud
SaaS presentation tools are great.
They're easy to use, comprehensive, and full of traditional Software features.
In today's cloud-based world, these solutions make life easier for people. We don't know about you, but we like it.
Software for Project Management
People began working remotely without signs or warnings before the 2020 COVID-19 pandemic.
Many organizations found it difficult to track projects and set deadlines.
With PMP software tools, teams can manage remote units and collaborate effectively.
App for Blockchain-Based Invoicing
This advanced billing and invoicing solution is for businesses and freelancers.
These blockchain-based apps can calculate taxes, manage debts, and manage transactions.
Intelligent contracts help blockchain track transactions more efficiently. It speeds up and improves invoice generation.
Software for Business Communications
Internal business messaging is tricky.
Top business software tools for communication can share files, collaborate on documents, host video conferences, and more.
Payroll Automation System
Software development also includes developing an automated payroll system.
These software systems reduce manual tasks for timely employee payments.
These tools help enterprise clients calculate total wages quickly, simplify tax calculations, improve record-keeping, and support better financial planning.
System for Detecting Data Leaks
Both businesses and individuals value data highly. Yahoo's data breach is dangerous because of this.
This area of software development can help people protect their data.
You can design an advanced data loss prevention system.
AI-based Retail System
AI-powered shopping systems are popular. The systems analyze customers' search and purchase patterns and store history and are equipped with a keyword database.
These systems offer many customers pre-loaded products.
AI-based shopping algorithms also help users make purchases.
Software for Detecting Plagiarism
Software can help ensure your projects are original and not plagiarized.
These tools detect plagiarized content that Google, media, and educational institutions don't like.
Software for Converting Audio to Text
Machine Learning converts speech to text automatically.
These programs can quickly transcribe cloud-based files.
Software for daily horoscopes
Daily and monthly horoscopes will continue to be popular.
Software platforms that can predict forecasts, calculate birth charts, and other astrology resources are good business ideas.
E-learning Programs
Traditional study methods are losing popularity as virtual schools proliferate and physical space shrinks.
Khan Academy online courses are the best way to keep learning.
Online education portals can boost your learning. If you want to start a tech startup, consider creating an e-learning program.
Conclusion
Software is booming. There's never been a better time to start a software development business, with so many people using computers and smartphones. This article lists eight business ideas for 2023. Consider these ideas if you're just starting out or looking to expand.

Darius Foroux
2 years ago
My financial life was changed by a single, straightforward mental model.
Prioritize big-ticket purchases
I've made several spending blunders. I get sick thinking about how much money I spent.
My financial mental model was poor back then.
Stoicism and mindfulness keep me from attaching to those feelings. It still hurts.
Until four or five years ago, I bought a new winter jacket every year.
Ten years ago, I spent twice as much. Now that I have a fantastic, warm winter parka, I don't even consider acquiring another one. No more spending. I'm not looking for jackets either.
Saving time and money by spending well is my thinking paradigm.
The philosophy is expressed in most languages. Cheap is expensive in the Netherlands. This applies beyond shopping.
In this essay, I will offer three examples of how this mental paradigm transformed my financial life.
Publishing books
In 2015, I presented and positioned my first book poorly.
I called the book Huge Life Success and made a funny Canva cover in 30 minutes. This:

That looks nothing like my present books. No logo or style. The book felt amateurish.
The book started bothering me a few weeks after publication. The advice was good, but it didn't appear professional. I studied the book business extensively.
I created a style for all my designs. Branding. Win Your Inner Wars was reissued a year later.
Title, cover, and description changed. Rearranging the chapters improved readability.
Seven years later, the book sells hundreds of copies a month. That taught me a lot.
Rushing to finish a project is enticing. Send it and move forward.
Avoid rushing everything. Relax. Develop your projects. Perform well. Perform the job well.
My first novel was underfunded and underworked. A bad book arrived. I then invested time and money in writing the greatest book I could.
That book still sells.
Traveling
I hate travel. Airports, flights, trains, and lines irritate me.
But, I enjoy traveling to beautiful areas.
I do it strangely. I make up travel rules. I never go to airports in summer. I hate being near airports on holidays. Unworthy.
No vacation packages for me. Those airline packages with a flight, shuttle, and hotel. I've had enough.
I try to avoid crowds and popular spots. July Paris? Nuts and bolts, please. Christmas in NYC? No, please keep me sane.
I fly business class behind. I accept upgrades upon check-in. I prefer driving. I drove from the Netherlands to southern Spain.
Thankfully, no lines. What if travel costs more? Thus? I enjoy it from the start. I start traveling then.
I rarely travel since I'm so difficult. One great excursion beats several average ones.
Personal effectiveness
New apps, tools, and strategies intrigue most productivity professionals.
No.
I researched years ago. I spent years investigating productivity in university.
I bought books, courses, applications, and tools. It was expensive and time-consuming.
Im finished. Productivity no longer costs me time or money. OK. I worked on it once and now follow my strategy.
I avoid new programs and systems. My stuff works. Why change winners?
Spending wisely saves time and money.
Spending wisely means spending once. Many people ignore productivity. It's understudied. No classes.
Some assume reading a few articles or a book is enough. Productivity is personal. You need a personal system.
Time invested is one-time. You can trust your system for life once you find it.
Concentrate on the expensive choices.
Life's short. Saving money quickly is enticing.
Spend less on groceries today. True. That won't fix your finances.
Adopt a lifestyle that makes you affluent over time. Consider major choices.
Are they causing long-term poverty? Are you richer?
Leasing cars comes to mind. The automobile costs a fortune today. The premium could accomplish a million nice things.
Focusing on important decisions makes life easier. Consider your future. You want to improve next year.
