More on Web3 & Crypto

Percy Bolmér
3 years ago
Ethereum No Longer Consumes A Medium-Sized Country's Electricity To Run
The Merge cut Ethereum's energy use by 99.5%.

The Crypto community celebrated on September 15, 2022. This day, Ethereum Merged. The entire blockchain successfully merged with the Beacon chain, and it was so smooth you barely noticed.
Many have waited, dreaded, and longed for this day.
Some investors feared the network would break down, while others envisioned a seamless merging.
Speculators predict a successful Merge will lead investors to Ethereum. This could boost Ethereum's popularity.
What Has Changed Since The Merge
The merging transitions Ethereum mainnet from PoW to PoS.
PoW sends a mathematical riddle to computers worldwide (miners). First miner to solve puzzle updates blockchain and is rewarded.
The puzzles sent are power-intensive to solve, so mining requires a lot of electricity. It's sent to every miner competing to solve it, requiring duplicate computation.
PoS allows investors to stake their coins to validate a new transaction. Instead of validating a whole block, you validate a transaction and get the fees.
You can validate instead of mine. A validator stakes 32 Ethereum. After staking, the validator can validate future blocks.
Once a validator validates a block, it's sent to a randomly selected group of other validators. This group verifies that a validator is not malicious and doesn't validate fake blocks.
This way, only one computer needs to solve or validate the transaction, instead of all miners. The validated block must be approved by a small group of validators, causing duplicate computation.
PoS is more secure because validating fake blocks results in slashing. You lose your bet tokens. If a validator signs a bad block or double-signs conflicting blocks, their ETH is burned.
Theoretically, Ethereum has one block every 12 seconds, so a validator forging a block risks burning 1 Ethereum for 12 seconds of transactions. This makes mistakes expensive and risky.
What Impact Does This Have On Energy Use?
Cryptocurrency is a natural calamity, sucking electricity and eating away at the earth one transaction at a time.
Many don't know the environmental impact of cryptocurrencies, yet it's tremendous.
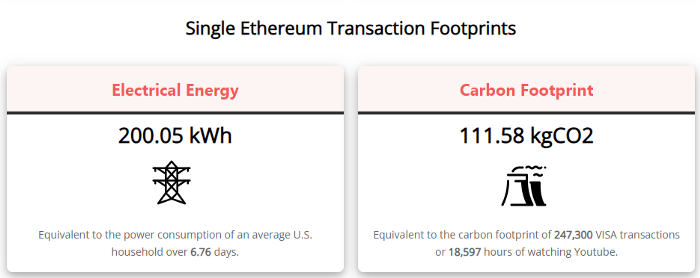
A single Ethereum transaction used to use 200 kWh and leave a large carbon imprint. This update reduces global energy use by 0.2%.
Ethereum will submit a challenge to one validator, and that validator will forward it to randomly selected other validators who accept it.
This reduces the needed computing power.
They expect a 99.5% reduction, therefore a single transaction should cost 1 kWh.
Carbon footprint is 0.58 kgCO2, or 1,235 VISA transactions.
This is a big Ethereum blockchain update.
I love cryptocurrency and Mother Earth.

CyberPunkMetalHead
3 years ago
It's all about the ego with Terra 2.0.
UST depegs and LUNA crashes 99.999% in a fraction of the time it takes the Moon to orbit the Earth.
Fat Man, a Terra whistle-blower, promises to expose Do Kwon's dirty secrets and shady deals.

The Terra community has voted to relaunch Terra LUNA on a new blockchain. The Terra 2.0 Pheonix-1 blockchain went live on May 28, 2022, and people were airdropped the new LUNA, now called LUNA, while the old LUNA became LUNA Classic.
Does LUNA deserve another chance? To answer this, or at least start a conversation about the Terra 2.0 chain's advantages and limitations, we must assess its fundamentals, ideology, and long-term vision.
Whatever the result, our analysis must be thorough and ruthless. A failure of this magnitude cannot happen again, so we must magnify every potential breaking point by 10.
Will UST and LUNA holders be compensated in full?
The obvious. First, and arguably most important, is to restore previous UST and LUNA holders' bags.
Terra 2.0 has 1,000,000,000,000 tokens to distribute.
25% of a community pool
Holders of pre-attack LUNA: 35%
10% of aUST holders prior to attack
Holders of LUNA after an attack: 10%
UST holders as of the attack: 20%
Every LUNA and UST holder has been compensated according to the above proposal.
According to self-reported data, the new chain has 210.000.000 tokens and a $1.3bn marketcap. LUNC and UST alone lost $40bn. The new token must fill this gap. Since launch:
LUNA holders collectively own $1b worth of LUNA if we subtract the 25% community pool airdrop from the current market cap and assume airdropped LUNA was never sold.
At the current supply, the chain must grow 40 times to compensate holders. At the current supply, LUNA must reach $240.
LUNA needs a full-on Bull Market to make LUNC and UST holders whole.
Who knows if you'll be whole? From the time you bought to the amount and price, there are too many variables to determine if Terra can cover individual losses.
The above distribution doesn't consider individual cases. Terra didn't solve individual cases. It would have been huge.
What does LUNA offer in terms of value?
UST's marketcap peaked at $18bn, while LUNC's was $41bn. LUNC and UST drove the Terra chain's value.
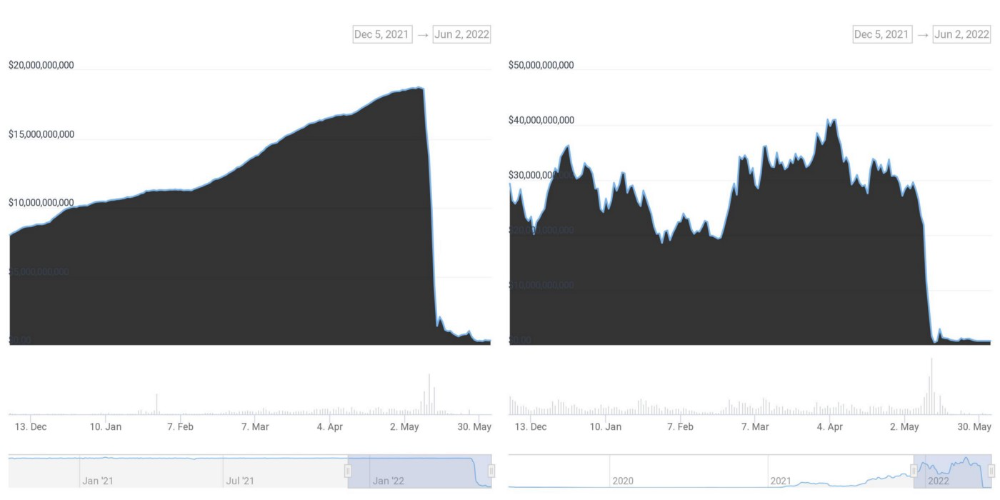
After it was confirmed (again) that algorithmic stablecoins are bad, Terra 2.0 will no longer support them.
Algorithmic stablecoins contributed greatly to Terra's growth and value proposition. Terra 2.0 has no product without algorithmic stablecoins.
Terra 2.0 has an identity crisis because it has no actual product. It's like Volkswagen faking carbon emission results and then stopping car production.
A project that has already lost the trust of its users and nearly all of its value cannot survive without a clear and in-demand use case.
Do Kwon, how about him?
Oh, the Twitter-caller-poor? Who challenges crypto billionaires to break his LUNA chain? Who dissolved Terra Labs South Korea before depeg? Arrogant guy?
That's not a good image for LUNA, especially when making amends. I think he should step down and let a nicer person be Terra 2.0's frontman.
The verdict
Terra has a terrific community with an arrogant, unlikeable leader. The new LUNA chain must grow 40 times before it can start making up its losses, and even then, not everyone's losses will be covered.
I won't invest in Terra 2.0 or other algorithmic stablecoins in the near future. I won't be near any Do Kwon-related project within 100 miles. My opinion.
Can Terra 2.0 be saved? Comment below.
Scott Hickmann
4 years ago
Welcome
Welcome to Integrity's Web3 community!
You might also like

Khyati Jain
3 years ago
By Engaging in these 5 Duplicitous Daily Activities, You Rapidly Kill Your Brain Cells
No, it’s not smartphones, overeating, or sugar.

Everyday practices affect brain health. Good brain practices increase memory and cognition.
Bad behaviors increase stress, which destroys brain cells.
Bad behaviors can reverse evolution and diminish the brain. So, avoid these practices for brain health.
1. The silent assassin
Introverts appreciated quarantine.
Before the pandemic, they needed excuses to remain home; thereafter, they had enough.
I am an introvert, and I didn’t hate quarantine. There are billions of people like me who avoid people.
Social relationships are important for brain health. Social anxiety harms your brain.
Antisocial behavior changes brains. It lowers IQ and increases drug abuse risk.
What you can do is as follows:
Make a daily commitment to engage in conversation with a stranger. Who knows, you might turn out to be your lone mate.
Get outside for at least 30 minutes each day.
Shop for food locally rather than online.
Make a call to a friend you haven't spoken to in a while.
2. Try not to rush things.
People love hustle culture. This economy requires a side gig to save money.
Long hours reduce brain health. A side gig is great until you burn out.
Work ages your wallet and intellect. Overworked brains age faster and lose cognitive function.
Working longer hours can help you make extra money, but it can harm your brain.
Side hustle but don't overwork.
What you can do is as follows:
Decide what hour you are not permitted to work after.
Three hours prior to night, turn off your laptop.
Put down your phone and work.
Assign due dates to each task.
3. Location is everything!
The environment may cause brain fog. High pollution can cause brain damage.
Air pollution raises Alzheimer's risk. Air pollution causes cognitive and behavioral abnormalities.
Polluted air can trigger early development of incurable brain illnesses, not simply lung harm.
Your city's air quality is uncontrollable. You may take steps to improve air quality.
In Delhi, schools and colleges are closed to protect pupils from polluted air. So I've adapted.
What you can do is as follows:
To keep your mind healthy and young, make an investment in a high-quality air purifier.
Enclose your windows during the day.
Use a N95 mask every day.
4. Don't skip this meal.
Fasting intermittently is trendy. Delaying breakfast to finish fasting is frequent.
Some skip breakfast and have a hefty lunch instead.
Skipping breakfast might affect memory and focus. Skipping breakfast causes low cognition, delayed responsiveness, and irritation.
Breakfast affects mood and productivity.
Intermittent fasting doesn't prevent healthy breakfasts.
What you can do is as follows:
Try to fast for 14 hours, then break it with a nutritious breakfast.
So that you can have breakfast in the morning, eat dinner early.
Make sure your breakfast is heavy in fiber and protein.
5. The quickest way to damage the health of your brain
Brain health requires water. 1% dehydration can reduce cognitive ability by 5%.
Cerebral fog and mental clarity might result from 2% brain dehydration. Dehydration shrinks brain cells.
Dehydration causes midday slumps and unproductivity. Water improves work performance.
Dehydration can harm your brain, so drink water throughout the day.
What you can do is as follows:
Always keep a water bottle at your desk.
Enjoy some tasty herbal teas.
With a big glass of water, begin your day.
Bring your own water bottle when you travel.
Conclusion
Bad habits can harm brain health. Low cognition reduces focus and productivity.
Unproductive work leads to procrastination, failure, and low self-esteem.
Avoid these harmful habits to optimize brain health and function.

Sarah Bird
3 years ago
Memes Help This YouTube Channel Earn Over $12k Per Month
Take a look at a YouTube channel making anything up to over $12k a month from making very simple videos.
And the best part? Its replicable by anyone. Basic videos can be generated for free without design abilities.
Join me as I deconstruct the channel to estimate how much they make, how they do it, and how you can too.
What Do They Do Exactly?
Happy Land posts memes with a simple caption they wrote. So, it's new. The videos are a slideshow of meme photos with stock music.
The site posts 12 times a day.
8-10-minute videos show 10 second images. Thus, each video needs 48-60 memes.
Memes are video titles (e.g. times a boyfriend was hilarious, back to school fails, funny restaurant signs).
Some stats about the channel:
Founded on October 30, 2020
873 videos were added.
81.8k subscribers
67,244,196 views of the video
What Value Are They Adding?
Everyone can find free memes online. This channel collects similar memes into a single video so you don't have to scroll or click for more. It’s right there, you just keep watching and more will come.
By theming it, the audience is prepared for the video's content.
If you want hilarious animal memes or restaurant signs, choose the video and you'll get up to 60 memes without having to look for them. Genius!
How much money do they make?
According to www.socialblade.com, the channel earns $800-12.8k (image shown in my home currency of GBP).
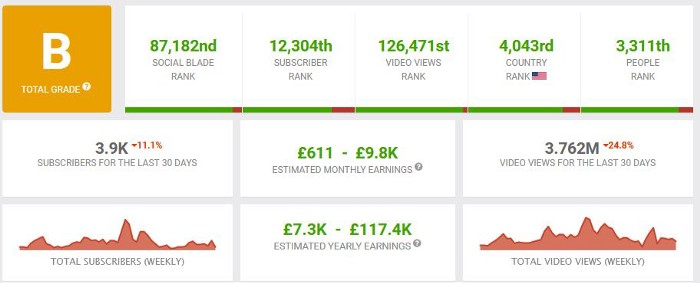
That's a crazy estimate, but it highlights the unbelievable potential of a channel that presents memes.
This channel thrives on quantity, thus putting out videos is necessary to keep the flow continuing and capture its audience's attention.
How Are the Videos Made?
Straightforward. Memes are added to a presentation without editing (so you could make this in PowerPoint or Keynote).
Each slide should include a unique image and caption. Set 10 seconds per slide.
Add music and post the video.
Finding enough memes for the material and theming is difficult, but if you enjoy memes, this is a fun job.
This case study should have shown you that you don't need expensive software or design expertise to make entertaining videos. Why not try fresh, easy-to-do ideas and see where they lead?

Bradley Vangelder
3 years ago
How we started and then quickly sold our startup
From a simple landing where we tested our MVP to a platform that distributes 20,000 codes per month, we learned a lot.

Starting point
Kwotet was my first startup. Everyone might post book quotes online.
I wanted a change.
Kwotet lacked attention, thus I felt stuck. After experiencing the trials of starting Kwotet, I thought of developing a waitlist service, but I required a strong co-founder.
I knew Dries from school, but we weren't close. He was an entrepreneurial programmer who worked a lot outside school. I needed this.
We brainstormed throughout school hours. We developed features to put us first. We worked until 3 am to launch this product.
Putting in the hours is KEY when building a startup

The instant that we lost our spark
In Belgium, college seniors do their internship in their last semester.
As we both made the decision to pick a quite challenging company, little time was left for Lancero.
Eventually, we lost interest. We lost the spark…
The only logical choice was to find someone with the same spark we started with to acquire Lancero.
And we did @ MicroAcquire.
Sell before your product dies. Make sure to profit from all the gains.
What did we do following the sale?
Not far from selling Lancero I lost my dad. I was about to start a new company. It was focused on positivity. I got none left at the time.
We still didn’t let go of the dream of becoming full-time entrepreneurs. As Dries launched the amazing company Plunk, and I’m still in the discovering stages of my next journey!

Dream!
You’re an entrepreneur if:
You're imaginative.
You enjoy disassembling and reassembling things.
You're adept at making new friends.
YOU HAVE DREAMS.
You don’t need to believe me if I tell you “everything is possible”… I wouldn't believe it myself if anyone told me this 2 years ago.
Until I started doing, living my dreams.
