NFT was used to serve a restraining order on an anonymous hacker.
The international law firm Holland & Knight used an NFT built and airdropped by its asset recovery team to serve a defendant in a hacking case.
The law firms Holland & Knight and Bluestone used a nonfungible token to serve a defendant in a hacking case with a temporary restraining order, marking the first documented legal process assisted by an NFT.
The so-called "service token" or "service NFT" was served to an unknown defendant in a hacking case involving LCX, a cryptocurrency exchange based in Liechtenstein that was hacked for over $8 million in January. The attack compromised the platform's hot wallets, resulting in the loss of Ether (ETH), USD Coin (USDC), and other cryptocurrencies, according to Cointelegraph at the time.
On June 7, LCX claimed that around 60% of the stolen cash had been frozen, with investigations ongoing in Liechtenstein, Ireland, Spain, and the United States. Based on a court judgment from the New York Supreme Court, Centre Consortium, a company created by USDC issuer Circle and crypto exchange Coinbase, has frozen around $1.3 million in USDC.
The monies were laundered through Tornado Cash, according to LCX, but were later tracked using "algorithmic forensic analysis." The organization was also able to identify wallets linked to the hacker as a result of the investigation.
In light of these findings, the law firms representing LCX, Holland & Knight and Bluestone, served the unnamed defendant with a temporary restraining order issued on-chain using an NFT. According to LCX, this system "was allowed by the New York Supreme Court and is an example of how innovation can bring legitimacy and transparency to a market that some say is ungovernable."
More on Web3 & Crypto

Shan Vernekar
3 years ago
How the Ethereum blockchain's transactions are carried out
Overview
Ethereum blockchain is a network of nodes that validate transactions. Any network node can be queried for blockchain data for free. To write data as a transition requires processing and writing to each network node's storage. Fee is paid in ether and is also called as gas.
We'll examine how user-initiated transactions flow across the network and into the blockchain.
Flow of transactions
A user wishes to move some ether from one external account to another. He utilizes a cryptocurrency wallet for this (like Metamask), which is a browser extension.
The user enters the desired transfer amount and the external account's address. He has the option to choose the transaction cost he is ready to pay.
Wallet makes use of this data, signs it with the user's private key, and writes it to an Ethereum node. Services such as Infura offer APIs that enable writing data to nodes. One of these services is used by Metamask. An example transaction is shown below. Notice the “to” address and value fields.
var rawTxn = {
nonce: web3.toHex(txnCount),
gasPrice: web3.toHex(100000000000),
gasLimit: web3.toHex(140000),
to: '0x633296baebc20f33ac2e1c1b105d7cd1f6a0718b',
value: web3.toHex(0),
data: '0xcc9ab24952616d6100000000000000000000000000000000000000000000000000000000'
};The transaction is written to the target Ethereum node's local TRANSACTION POOL. It informed surrounding nodes of the new transaction, and those nodes reciprocated. Eventually, this transaction is received by and written to each node's local TRANSACTION pool.
The miner who finds the following block first adds pending transactions (with a higher gas cost) from the nearby TRANSACTION POOL to the block.
The transactions written to the new block are verified by other network nodes.
A block is added to the main blockchain after there is consensus and it is determined to be genuine. The local blockchain is updated with the new node by additional nodes as well.
Block mining begins again next.
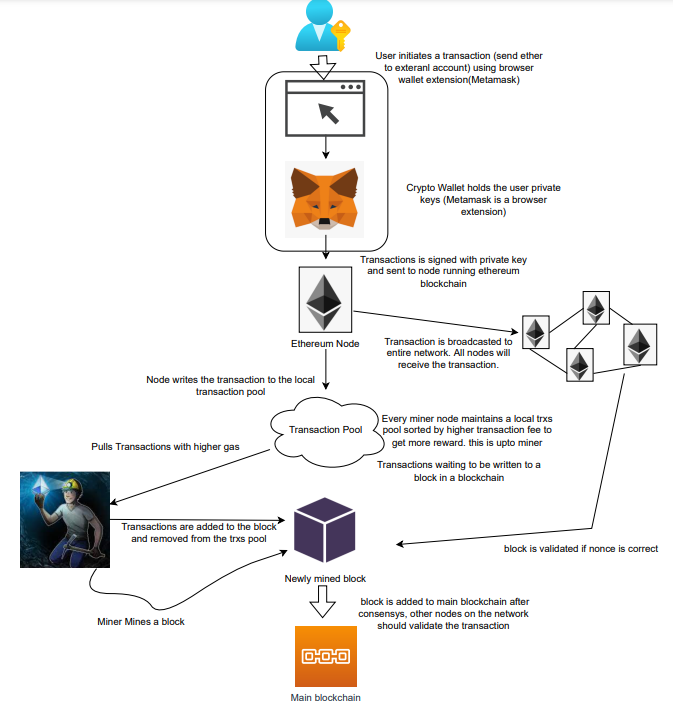
The image above shows how transactions go via the network and what's needed to submit them to the main block chain.
References
ethereum.org/transactions How Ethereum transactions function, their data structure, and how to send them via app. ethereum.org

CyberPunkMetalHead
3 years ago
I talked to ChatGPT about the adoption of cryptocurrencies.

OpenAI's ChatGPT is an amazing AI-powered chatbot. It can write poetry, fiction, and marketing ideas. I was impressed how well ChatGPT followed the interview, albeit there were a few classics “I’m afraid I can’t do that”.
Full interview below.
Me: I'm your interviewer. We'll discuss crypto. Thanks for being interviewed. What do you think about cryptocurrency?
CGPT: Cryptocurrency is an innovative technology that could transform money and financial activities. It might boost the efficiency and security of financial institutions and let consumers deal directly without banks. Cryptocurrency is still a new and untested technology with many unknowns and hurdles before it can be broadly accepted.
Me: Over 22,000 cryptocurrencies exist, and many have little use. We need how much cryptocurrencies?
CGPT: The appropriate quantity will rely on a multitude of factors, including each cryptocurrency's use cases, adoption rate, and market rivalry. Only a few cryptocurrencies will likely receive widespread adoption and be successful. Many existing cryptocurrencies may not survive since they can't deliver new or valued solutions or compete with more established cryptocurrencies.
Me: Will cryptocurrencies grow? What's next for worldwide adoption?
CGPT: It's hard to forecast the future of cryptocurrencies because the acceptance of new technologies is unpredictable. I believe cryptocurrencies will expand and acquire popularity in the future years. Regulatory ambiguity, security concerns, and scalability issues must be overcome for this to happen. Cryptocurrency companies and organizations must engage together with governments and authorities to address these obstacles and establish a growth-friendly climate. Continued innovation and improvement of the technology, including public education and awareness, will drive acceptance.
Me: Do bear markets affect bitcoin adoption?
CGPT: On the one hand, a bear market might induce uncertainty and hesitation among potential consumers. Bear markets can present opportunities for long-term investors who can acquire cryptocurrencies at cheaper prices and are more likely to hang onto their assets. A bear market can also test the tenacity and power of the underlying technology and community, which can boost long-term confidence and adoption. A bear market might have profound and nuanced effects on bitcoin adoption.
Me: What are some likely outcomes if Bitcoin reaches $100,000 by next year?
CGPT: If Bitcoin saw rapid growth, it would undoubtedly have repercussions for the cryptocurrency market and economy. Possible scenarios include increased public interest and awareness of cryptocurrency, a surge in demand for Bitcoin and other cryptocurrencies, and a growth in the cryptocurrency industry's market value. By shifting their focus and cash to the cryptocurrency market, investors and traders may also affect other asset classes, such as traditional equities and commodities. Governments and financial organizations may focus more on the cryptocurrency sector as they try to grasp Bitcoin's rapid rise.
Me: Will other countries accept crypto as currency?
CGPT: It's hard to say if additional governments will adopt cryptocurrencies as legal tender. Some countries have recognized the promise of bitcoin and are exploring its use, while others are cautious. Adoption of bitcoin as legal cash may vary by country, based on financial infrastructure, rules, and political atmosphere. As cryptocurrency technology evolves and becomes more accepted, more governments may embrace it as legal tender.
Me: Final question: will the recent cryptocurrency hacks affect long term adoption?
CGPT: Hacks might tarnish cryptocurrency's reputation and public faith in its security, the technology underpinning it is continually improving. Many cryptocurrency projects have developed strong security mechanisms to prevent hacks and other dangers, and these safeguards will undoubtedly improve over time. The decentralized nature of cryptocurrency makes it more resistant to attacks. Hacks and other security breaches are a concern, but they may not affect cryptocurrency adoption.
James Howell
3 years ago
Which Metaverse Is Better, Decentraland or Sandbox?
The metaverse is the most commonly used term in current technology discussions. While the entire tech ecosystem awaits the metaverse's full arrival, defining it is difficult. Imagine the internet in the '80s! The metaverse is a three-dimensional virtual world where users can interact with digital solutions and each other as digital avatars.
The metaverse is a three-dimensional virtual world where users can interact with digital solutions and each other as digital avatars.
Among the metaverse hype, the Decentraland vs Sandbox debate has gained traction. Both are decentralized metaverse platforms with no central authority. So, what's the difference and which is better? Let us examine the distinctions between Decentraland and Sandbox.
2 Popular Metaverse Platforms Explained
The first step in comparing sandbox and Decentraland is to outline the definitions. Anyone keeping up with the metaverse news has heard of the two current leaders. Both have many similarities, but also many differences. Let us start with defining both platforms to see if there is a winner.
Decentraland
Decentraland, a fully immersive and engaging 3D metaverse, launched in 2017. It allows players to buy land while exploring the vast virtual universe. Decentraland offers a wide range of activities for its visitors, including games, casinos, galleries, and concerts. It is currently the longest-running metaverse project.
Decentraland began with a $24 million ICO and went public in 2020. The platform's virtual real estate parcels allow users to create a variety of experiences. MANA and LAND are two distinct tokens associated with Decentraland. MANA is the platform's native ERC-20 token, and users can burn MANA to get LAND, which is ERC-721 compliant. The MANA coin can be used to buy avatars, wearables, products, and names on Decentraland.
Sandbox
Sandbox, the next major player, began as a blockchain-based virtual world in 2011 and migrated to a 3D gaming platform in 2017. The virtual world allows users to create, play, own, and monetize their virtual experiences. Sandbox aims to empower artists, creators, and players in the blockchain community to customize the platform. Sandbox gives the ideal means for unleashing creativity in the development of the modern gaming ecosystem.
The project combines NFTs and DAOs to empower a growing community of gamers. A new play-to-earn model helps users grow as gamers and creators. The platform offers a utility token, SAND, which is required for all transactions.
What are the key points from both metaverse definitions to compare Decentraland vs sandbox?
It is ideal for individuals, businesses, and creators seeking new artistic, entertainment, and business opportunities. It is one of the rapidly growing Decentralized Autonomous Organization projects. Holders of MANA tokens also control the Decentraland domain.
Sandbox, on the other hand, is a blockchain-based virtual world that runs on the native token SAND. On the platform, users can create, sell, and buy digital assets and experiences, enabling blockchain-based gaming. Sandbox focuses on user-generated content and building an ecosystem of developers.
Sandbox vs. Decentraland
If you try to find what is better Sandbox or Decentraland, then you might struggle with only the basic definitions. Both are metaverse platforms offering immersive 3D experiences. Users can freely create, buy, sell, and trade digital assets. However, both have significant differences, especially in MANA vs SAND.
For starters, MANA has a market cap of $5,736,097,349 versus $4,528,715,461, giving Decentraland an advantage.
The MANA vs SAND pricing comparison is also noteworthy. A SAND is currently worth $3664, while a MANA is worth $2452.
The value of the native tokens and the market capitalization of the two metaverse platforms are not enough to make a choice. Let us compare Sandbox vs Decentraland based on the following factors.
Workstyle
The way Decentraland and Sandbox work is one of the main comparisons. From a distance, they both appear to work the same way. But there's a lot more to learn about both platforms' workings. Decentraland has 90,601 digital parcels of land.
Individual parcels of virtual real estate or estates with multiple parcels of land are assembled. It also has districts with similar themes and plazas, which are non-tradeable parcels owned by the community. It has three token types: MANA, LAND, and WEAR.
Sandbox has 166,464 plots of virtual land that can be grouped into estates. Estates are owned by one person, while districts are owned by two or more people. The Sandbox metaverse has four token types: SAND, GAMES, LAND, and ASSETS.
Age
The maturity of metaverse projects is also a factor in the debate. Decentraland is clearly the winner in terms of maturity. It was the first solution to create a 3D blockchain metaverse. Decentraland made the first working proof of concept public. However, Sandbox has only made an Alpha version available to the public.
Backing
The MANA vs SAND comparison would also include support for both platforms. Digital Currency Group, FBG Capital, and CoinFund are all supporters of Decentraland. It has also partnered with Polygon, the South Korean government, Cyberpunk, and Samsung.
SoftBank, a Japanese multinational conglomerate focused on investment management, is another major backer. Sandbox has the backing of one of the world's largest investment firms, as well as Slack and Uber.
Compatibility
Wallet compatibility is an important factor in comparing the two metaverse platforms. Decentraland currently has a competitive advantage. How? Both projects' marketplaces accept ERC-20 wallets. However, Decentraland has recently improved by bridging with Walletconnect. So it can let Polygon users join Decentraland.
Scalability
Because Sandbox and Decentraland use the Ethereum blockchain, scalability is an issue. Both platforms' scalability is constrained by volatile tokens and high gas fees. So, scalability issues can hinder large-scale adoption of both metaverse platforms.
Buying Land
Decentraland vs Sandbox comparisons often include virtual real estate. However, the ability to buy virtual land on both platforms defines the user experience and differentiates them. In this case, Sandbox offers better options for users to buy virtual land by combining OpenSea and Sandbox. In fact, Decentraland users can only buy from the MANA marketplace.
Innovation
The rate of development distinguishes Sandbox and Decentraland. Both platforms have been developing rapidly new features. However, Sandbox wins by adopting Polygon NFT layer 2 solutions, which consume almost 100 times less energy than Ethereum.
Collaborations
The platforms' collaborations are the key to determining "which is better Sandbox or Decentraland." Adoption of metaverse platforms like the two in question can be boosted by association with reputable brands. Among the partners are Atari, Cyberpunk, and Polygon. Rather, Sandbox has partnered with well-known brands like OpenSea, CryptoKitties, The Walking Dead, Snoop Dogg, and others.
Platform Adaptivity
Another key feature that distinguishes Sandbox and Decentraland is the ease of use. Sandbox clearly wins in terms of platform access. It allows easy access via social media, email, or a Metamask wallet. However, Decentraland requires a wallet connection.
Prospects
The future development plans also play a big role in defining Sandbox vs Decentraland. Sandbox's future development plans include bringing the platform to mobile devices. This includes consoles like PlayStation and Xbox. By the end of 2023, the platform expects to have around 5000 games.
Decentraland, on the other hand, has no set plan. In fact, the team defines the decisions that appear to have value. They plan to add celebrities, creators, and brands soon, along with NFT ads and drops.
Final Words
The comparison of Decentraland vs Sandbox provides a balanced view of both platforms. You can see how difficult it is to determine which decentralized metaverse is better now. Sandbox is still in Alpha, whereas Decentraland has a working proof of concept.
Sandbox, on the other hand, has better graphics and is backed by some big names. But both have a long way to go in the larger decentralized metaverse.
You might also like

Ethan Siegel
2 years ago
How you view the year will change after using this one-page calendar.

No other calendar is simpler, smaller, and reusable year after year. It works and is used here.
Most of us discard and replace our calendars annually. Each month, we move our calendar ahead another page, thus if we need to know which day of the week corresponds to a given day/month combination, we have to calculate it or flip forward/backward to the corresponding month. Questions like:
What day does this year's American Thanksgiving fall on?
Which months contain a Friday the thirteenth?
When is July 4th? What day of the week?
Alternatively, what day of the week is Christmas?
They're hard to figure out until you switch to the right month or look up all the months.
However, mathematically, the answers to these questions or any question that requires matching the day of the week with the day/month combination in a year are predictable, basic, and easy to work out. If you use this one-page calendar instead of a 12-month calendar, it lasts the whole year and is easy to alter for future years. Let me explain.
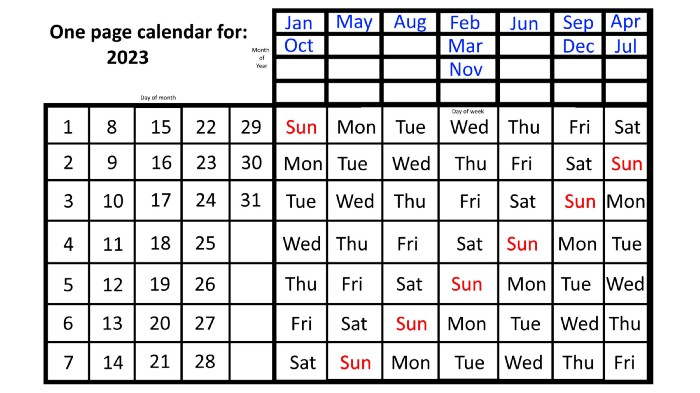
The 2023 one-page calendar is above. The days of the month are on the lower left, which works for all months if you know that:
There are 31 days in January, March, May, July, August, October, and December.
All of the months of April, June, September, and November have 30 days.
And depending on the year, February has either 28 days (in non-leap years) or 29 days (in leap years).
If you know this, this calendar makes it easy to match the day/month of the year to the weekday.
Here are some instances. American Thanksgiving is always on the fourth Thursday of November. You'll always know the month and day of the week, but the date—the day in November—changes each year.
On any other calendar, you'd have to flip to November to see when the fourth Thursday is. This one-page calendar only requires:
pick the month of November in the top-right corner to begin.
drag your finger down until Thursday appears,
then turn left and follow the monthly calendar until you reach the fourth Thursday.
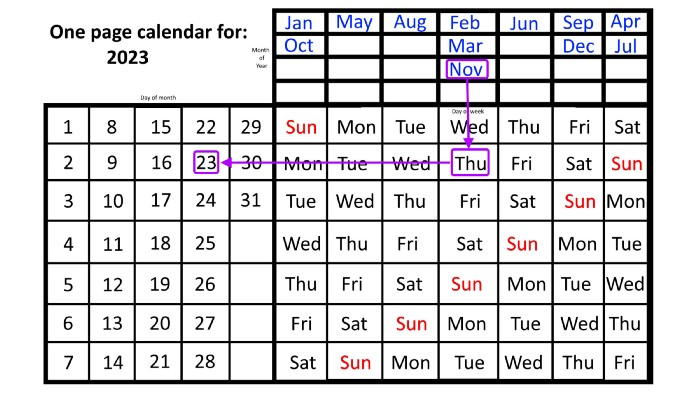
It's obvious: 2023 is the 23rd American Thanksgiving. For every month and day-of-the-week combination, start at the month, drag your finger down to the desired day, and then move to the left to see which dates match.
What if you knew the day of the week and the date of the month, but not the month(s)?
A different method using the same one-page calendar gives the answer. Which months have Friday the 13th this year? Just:
begin on the 13th of the month, the day you know you desire,
then swipe right with your finger till Friday appears.
and then work your way up until you can determine which months the specific Friday the 13th falls under.
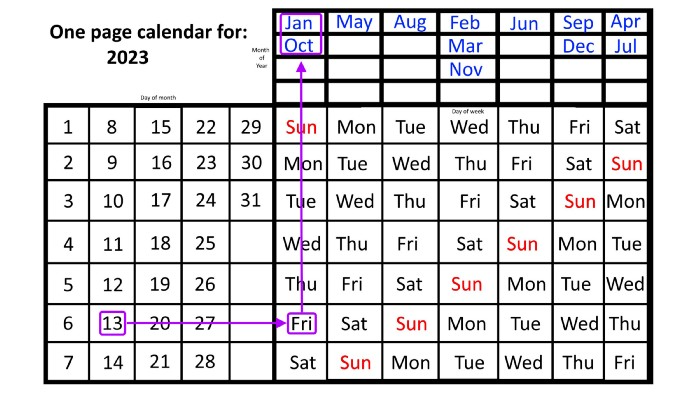
One Friday the 13th occurred in January 2023, and another will occur in October.
The most typical reason to consult a calendar is when you know the month/day combination but not the day of the week.
Compared to single-month calendars, the one-page calendar excels here. Take July 4th, for instance. Find the weekday here:
beginning on the left on the fourth of the month, as you are aware,
also begin with July, the month of the year you are most familiar with, at the upper right,
you should move your two fingers in the opposite directions till they meet: on a Tuesday in 2023.
That's how you find your selected day/month combination's weekday.
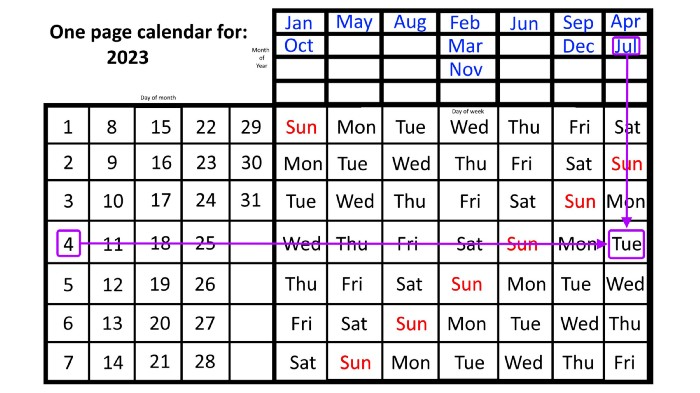
Another example: Christmas. Christmas Day is always December 25th, however unless your conventional calendar is open to December of your particular year, a question like "what day of the week is Christmas?" difficult to answer.
Unlike the one-page calendar!
Remember the left-hand day of the month. Top-right, you see the month. Put two fingers, one from each hand, on the date (25th) and the month (December). Slide the day hand to the right and the month hand downwards until they touch.
They meet on Monday—December 25, 2023.
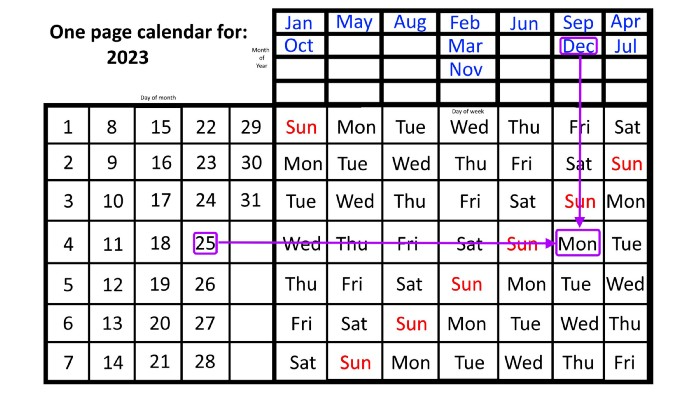
For 2023, that's fine, but what happens in 2024? Even worse, what if we want to know the day-of-the-week/day/month combo many years from now?
I think the one-page calendar shines here.
Except for the blue months in the upper-right corner of the one-page calendar, everything is the same year after year. The months also change in a consistent fashion.
Each non-leap year has 365 days—one more than a full 52 weeks (which is 364). Since January 1, 2023 began on a Sunday and 2023 has 365 days, we immediately know that December 31, 2023 will conclude on a Sunday (which you can confirm using the one-page calendar) and that January 1, 2024 will begin on a Monday. Then, reorder the months for 2024, taking in mind that February will have 29 days in a leap year.
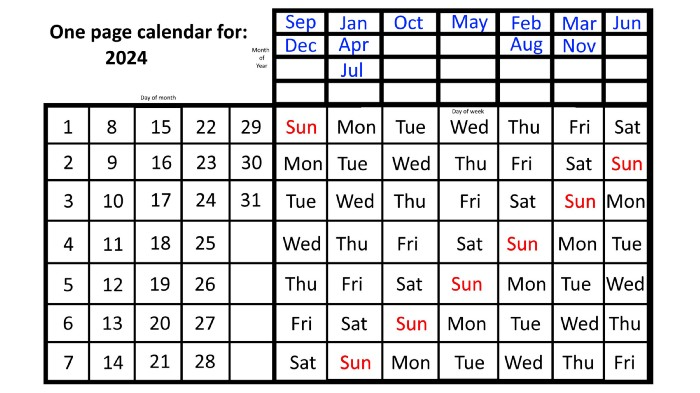
Please note the differences between 2023 and 2024 month placement. In 2023:
October and January began on the same day of the week.
On the following Monday of the week, May began.
August started on the next day,
then the next weekday marked the start of February, March, and November, respectively.
Unlike June, which starts the following weekday,
While September and December start on the following day of the week,
Lastly, April and July start one extra day later.
Since 2024 is a leap year, February has 29 days, disrupting the rhythm. Month placements change to:
The first day of the week in January, April, and July is the same.
October will begin the following day.
Possibly starting the next weekday,
February and August start on the next weekday,
beginning on the following day of the week between March and November,
beginning the following weekday in June,
and commencing one more day of the week after that, September and December.
Due to the 366-day leap year, 2025 will start two days later than 2024 on January 1st.
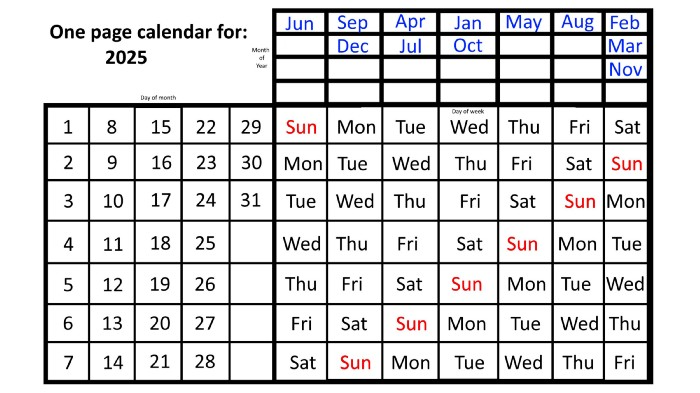
Now, looking at the 2025 calendar, you can see that the 2023 pattern of which months start on which days is repeated! The sole variation is a shift of three days-of-the-week ahead because 2023 had one more day (365) than 52 full weeks (364), and 2024 had two more days (366). Again,
On Wednesday this time, January and October begin on the same day of the week.
Although May begins on Thursday,
August begins this Friday.
March, November, and February all begin on a Saturday.
Beginning on a Sunday in June
Beginning on Monday are September and December,
and on Tuesday, April and July begin.
In 2026 and 2027, the year will commence on a Thursday and a Friday, respectively.
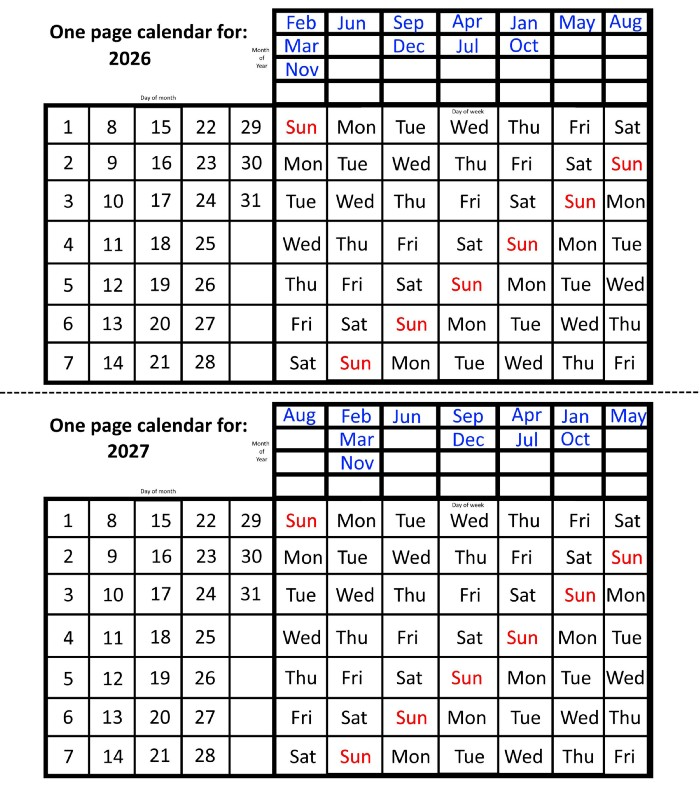
We must return to our leap year monthly arrangement in 2028. Yes, January 1, 2028 begins on a Saturday, but February, which begins on a Tuesday three days before January, will have 29 days. Thus:
Start dates for January, April, and July are all Saturdays.
Given that October began on Sunday,
Although May starts on a Monday,
beginning on a Tuesday in February and August,
Beginning on a Wednesday in March and November,
Beginning on Thursday, June
and Friday marks the start of September and December.
This is great because there are only 14 calendar configurations: one for each of the seven non-leap years where January 1st begins on each of the seven days of the week, and one for each of the seven leap years where it begins on each day of the week.
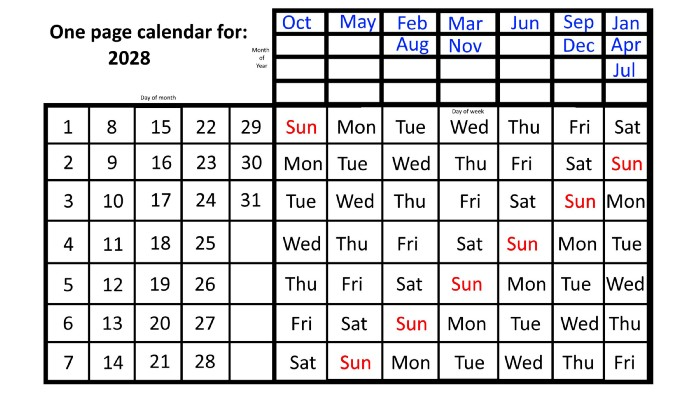
The 2023 calendar will function in 2034, 2045, 2051, 2062, 2073, 2079, 2090, 2102, 2113, and 2119. Except when passing over a non-leap year that ends in 00, like 2100, the repeat time always extends to 12 years or shortens to an extra 6 years.
The pattern is repeated in 2025's calendar in 2031, 2042, 2053, 2059, 2070, 2081, 2087, 2098, 2110, and 2121.
The extra 6-year repeat at the end of the century on the calendar for 2026 will occur in the years 2037, 2043, 2054, 2065, 2071, 2082, 2093, 2099, 2105, and 2122.
The 2027s calendar repeats in 2038, 2049, 2055, 2066, 2077, 2083, 2094, 2100, 2106, and 2117, almost exactly matching the 2026s pattern.
For leap years, the recurrence pattern is every 28 years when not passing a non-leap year ending in 00, or 12 or 40 years when we do. 2024's calendar repeats in 2052, 2080, 2120, 2148, 2176, and 2216; 2028's in 2056, 2084, 2124, 2152, 2180, and 2220.
Knowing January 1st and whether it's a leap year lets you construct a one-page calendar for any year. Try it—you might find it easier than any other alternative!

Patryk Nawrocki
3 years ago
7 things a new UX/UI designer should know
If I could tell my younger self a few rules, they would boost my career.
1. Treat design like medicine; don't get attached.

If it doesn't help, you won't be angry, but you'll try to improve it. Designers blame others if they don't like the design, but the rule is the same: we solve users' problems. You're not your design, and neither are they. Be humble with your work because your assumptions will often be wrong and users will behave differently.
2. Consider your design flawed.

Disagree with yourself, then defend your ideas. Most designers forget to dig deeper into a pattern, screen, button, or copywriting. If someone asked, "Have you considered alternatives? How does this design stack up? Here's a functional UX checklist to help you make design decisions.
3. Codeable solutions.

If your design requires more developer time, consider whether it's worth spending more money to code something with a small UX impact. Overthinking problems and designing abstract patterns is easy. Sometimes you see something on dribbble or bechance and try to recreate it, but it's not worth it. Here's my article on it.
4. Communication changes careers

Designers often talk with users, clients, companies, developers, and other designers. How you talk and present yourself can land you a job. Like driving or swimming, practice it. Success requires being outgoing and friendly. If I hadn't said "hello" to a few people, I wouldn't be where I am now.
5. Ignorance of the law is not an excuse.

Copyright, taxation How often have you used an icon without checking its license? If you use someone else's work in your project, the owner can cause you a lot of problems — paying a lot of money isn't worth it. Spend a few hours reading about copyrights, client agreements, and taxes.
6. Always test your design

If nobody has seen or used my design, it's not finished. Ask friends about prototypes. Testing reveals how wrong your assumptions were. Steve Krug, one of the authorities on this topic will tell you more about how to do testing.
7. Run workshops

A UX designer's job involves talking to people and figuring out what they need, which is difficult because they usually don't know. Organizing teamwork sessions is a powerful skill, but you must also be a good listener. Your job is to help a quiet, introverted developer express his solution and control the group. AJ Smart has more on workshops here.

Jess Rifkin
3 years ago
As the world watches the Russia-Ukraine border situation, This bill would bar aid to Ukraine until the Mexican border is secured.
Although Mexico and Ukraine are thousands of miles apart, this legislation would link their responses.
Context
Ukraine was a Soviet republic until 1991. A significant proportion of the population, particularly in the east, is ethnically Russian. In February, the Russian military invaded Ukraine, intent on overthrowing its democratically elected government.
This could be the biggest European land invasion since WWII. In response, President Joe Biden sent 3,000 troops to NATO countries bordering Ukraine to help with Ukrainian refugees, with more troops possible if the situation worsened.
In July 2021, the US Border Patrol reported its highest monthly encounter total since March 2000. Some Republicans compare Biden's response to the Mexican border situation to his response to the Ukrainian border situation, though the correlation is unclear.
What the bills do
Two new Republican bills seek to link the US response to Ukraine to the situation in Mexico.
The Secure America's Borders First Act would prohibit federal funding for Ukraine until the US-Mexico border is “operationally controlled,” including a wall as promised by former President Donald Trump. (The bill even mandates a 30-foot-high wall.)
The USB (Ukraine and Southern Border) Act, introduced on February 8 by Rep. Matt Rosendale (R-MT0), would allow the US to support Ukraine, but only if the number of Armed Forces deployed there is less than the number deployed to the Mexican border. Madison Cawthorne introduced H.R. 6665 on February 9th (R-NC11).
What backers say
Supporters argue that even if the US should militarily assist Ukraine, our own domestic border situation should take precedence.
After failing to secure our own border and protect our own territorial integrity, ‘America Last' politicians on both sides of the aisle now tell us that we must do so for Ukraine. “Before rushing America into another foreign conflict over an Eastern European nation's border thousands of miles from our shores, they should first secure our southern border.”
“If Joe Biden truly cared about Americans, he would prioritize national security over international affairs,” Rep. Cawthorn said in a separate press release. The least we can do to secure our own country is send the same number of troops to the US-Mexico border to assist our border patrol agents working diligently to secure America.
What opponents say
The president has defended his Ukraine and Mexico policies, stating that both seek peace and diplomacy.
Our nations [the US and Mexico] have a long and complicated history, and we haven't always been perfect neighbors, but we have seen the power and purpose of cooperation,” Biden said in 2021. “We're safer when we work together, whether it's to manage our shared border or stop the pandemic. [In both the Obama and Biden administration], we made a commitment that we look at Mexico as an equal, not as somebody who is south of our border.”
No mistake: If Russia goes ahead with its plans, it will be responsible for a catastrophic and unnecessary war of choice. To protect our collective security, the United States and our allies are ready to defend every inch of NATO territory. We won't send troops into Ukraine, but we will continue to support the Ukrainian people... But, I repeat, Russia can choose diplomacy. It is not too late to de-escalate and return to the negotiating table.”
Odds of passage
The Secure America's Borders First Act has nine Republican sponsors. Either the House Armed Services or Foreign Affairs Committees may vote on it.
Rep. Paul Gosar, a Republican, co-sponsored the USB Act (R-AZ4). The House Armed Services Committee may vote on it.
With Republicans in control, passage is unlikely.
