More on Web3 & Crypto

Farhan Ali Khan
2 years ago
Introduction to Zero-Knowledge Proofs: The Art of Proving Without Revealing
Zero-Knowledge Proofs for Beginners
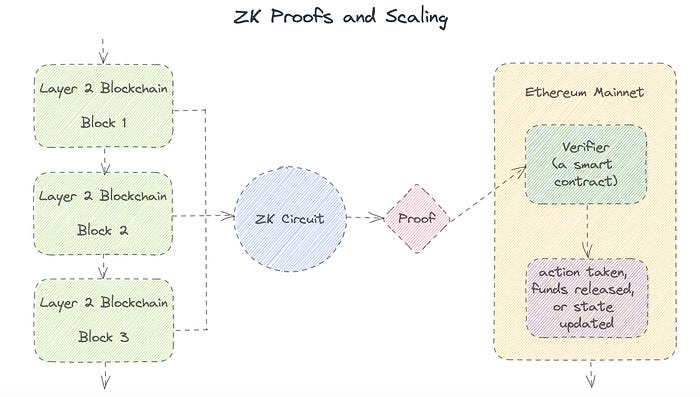
Published here originally.
Introduction
I Spy—did you play as a kid? One person chose a room object, and the other had to guess it by answering yes or no questions. I Spy was entertaining, but did you know it could teach you cryptography?
Zero Knowledge Proofs let you show your pal you know what they picked without exposing how. Math replaces electronics in this secret spy mission. Zero-knowledge proofs (ZKPs) are sophisticated cryptographic tools that allow one party to prove they have particular knowledge without revealing it. This proves identification and ownership, secures financial transactions, and more. This article explains zero-knowledge proofs and provides examples to help you comprehend this powerful technology.
What is a Proof of Zero Knowledge?
Zero-knowledge proofs prove a proposition is true without revealing any other information. This lets the prover show the verifier that they know a fact without revealing it. So, a zero-knowledge proof is like a magician's trick: the prover proves they know something without revealing how or what. Complex mathematical procedures create a proof the verifier can verify.
Want to find an easy way to test it out? Try out with tis awesome example! ZK Crush
Describe it as if I'm 5
Alex and Jack found a cave with a center entrance that only opens when someone knows the secret. Alex knows how to open the cave door and wants to show Jack without telling him.
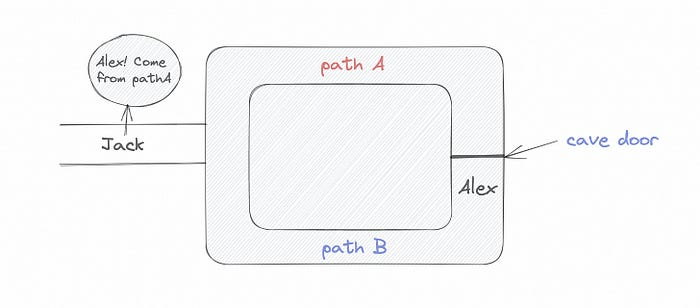
Alex and Jack name both pathways (let’s call them paths A and B).
In the first phase, Alex is already inside the cave and is free to select either path, in this case A or B.
As Alex made his decision, Jack entered the cave and asked him to exit from the B path.
Jack can confirm that Alex really does know the key to open the door because he came out for the B path and used it.
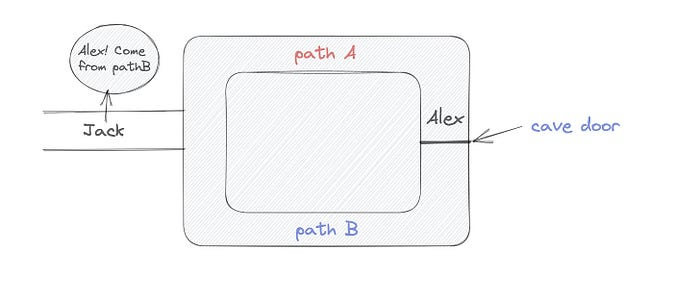
To conclude, Alex and Jack repeat:
Alex walks into the cave.
Alex follows a random route.
Jack walks into the cave.
Alex is asked to follow a random route by Jack.
Alex follows Jack's advice and heads back that way.
What is a Zero Knowledge Proof?
At a high level, the aim is to construct a secure and confidential conversation between the prover and the verifier, where the prover convinces the verifier that they have the requisite information without disclosing it. The prover and verifier exchange messages and calculate in each round of the dialogue.
The prover uses their knowledge to prove they have the information the verifier wants during these rounds. The verifier can verify the prover's truthfulness without learning more by checking the proof's mathematical statement or computation.
Zero knowledge proofs use advanced mathematical procedures and cryptography methods to secure communication. These methods ensure the evidence is authentic while preventing the prover from creating a phony proof or the verifier from extracting unnecessary information.
ZK proofs require examples to grasp. Before the examples, there are some preconditions.
Criteria for Proofs of Zero Knowledge
Completeness: If the proposition being proved is true, then an honest prover will persuade an honest verifier that it is true.
Soundness: If the proposition being proved is untrue, no dishonest prover can persuade a sincere verifier that it is true.
Zero-knowledge: The verifier only realizes that the proposition being proved is true. In other words, the proof only establishes the veracity of the proposition being supported and nothing more.
The zero-knowledge condition is crucial. Zero-knowledge proofs show only the secret's veracity. The verifier shouldn't know the secret's value or other details.
Example after example after example
To illustrate, take a zero-knowledge proof with several examples:
Initial Password Verification Example
You want to confirm you know a password or secret phrase without revealing it.
Use a zero-knowledge proof:
You and the verifier settle on a mathematical conundrum or issue, such as figuring out a big number's components.
The puzzle or problem is then solved using the hidden knowledge that you have learned. You may, for instance, utilize your understanding of the password to determine the components of a particular number.
You provide your answer to the verifier, who can assess its accuracy without knowing anything about your private data.
You go through this process several times with various riddles or issues to persuade the verifier that you actually are aware of the secret knowledge.
You solved the mathematical puzzles or problems, proving to the verifier that you know the hidden information. The proof is zero-knowledge since the verifier only sees puzzle solutions, not the secret information.
In this scenario, the mathematical challenge or problem represents the secret, and solving it proves you know it. The evidence does not expose the secret, and the verifier just learns that you know it.
My simple example meets the zero-knowledge proof conditions:
Completeness: If you actually know the hidden information, you will be able to solve the mathematical puzzles or problems, hence the proof is conclusive.
Soundness: The proof is sound because the verifier can use a publicly known algorithm to confirm that your answer to the mathematical conundrum or difficulty is accurate.
Zero-knowledge: The proof is zero-knowledge because all the verifier learns is that you are aware of the confidential information. Beyond the fact that you are aware of it, the verifier does not learn anything about the secret information itself, such as the password or the factors of the number. As a result, the proof does not provide any new insights into the secret.
Explanation #2: Toss a coin.
One coin is biased to come up heads more often than tails, while the other is fair (i.e., comes up heads and tails with equal probability). You know which coin is which, but you want to show a friend you can tell them apart without telling them.
Use a zero-knowledge proof:
One of the two coins is chosen at random, and you secretly flip it more than once.
You show your pal the following series of coin flips without revealing which coin you actually flipped.
Next, as one of the two coins is flipped in front of you, your friend asks you to tell which one it is.
Then, without revealing which coin is which, you can use your understanding of the secret order of coin flips to determine which coin your friend flipped.
To persuade your friend that you can actually differentiate between the coins, you repeat this process multiple times using various secret coin-flipping sequences.
In this example, the series of coin flips represents the knowledge of biased and fair coins. You can prove you know which coin is which without revealing which is biased or fair by employing a different secret sequence of coin flips for each round.
The evidence is zero-knowledge since your friend does not learn anything about which coin is biased and which is fair other than that you can tell them differently. The proof does not indicate which coin you flipped or how many times you flipped it.
The coin-flipping example meets zero-knowledge proof requirements:
Completeness: If you actually know which coin is biased and which is fair, you should be able to distinguish between them based on the order of coin flips, and your friend should be persuaded that you can.
Soundness: Your friend may confirm that you are correctly recognizing the coins by flipping one of them in front of you and validating your answer, thus the proof is sound in that regard. Because of this, your acquaintance can be sure that you are not just speculating or picking a coin at random.
Zero-knowledge: The argument is that your friend has no idea which coin is biased and which is fair beyond your ability to distinguish between them. Your friend is not made aware of the coin you used to make your decision or the order in which you flipped the coins. Consequently, except from letting you know which coin is biased and which is fair, the proof does not give any additional information about the coins themselves.
Figure out the prime number in Example #3.
You want to prove to a friend that you know their product n=pq without revealing p and q. Zero-knowledge proof?
Use a variant of the RSA algorithm. Method:
You determine a new number s = r2 mod n by computing a random number r.
You email your friend s and a declaration that you are aware of the values of p and q necessary for n to equal pq.
A random number (either 0 or 1) is selected by your friend and sent to you.
You send your friend r as evidence that you are aware of the values of p and q if e=0. You calculate and communicate your friend's s/r if e=1.
Without knowing the values of p and q, your friend can confirm that you know p and q (in the case where e=0) or that s/r is a legitimate square root of s mod n (in the situation where e=1).
This is a zero-knowledge proof since your friend learns nothing about p and q other than their product is n and your ability to verify it without exposing any other information. You can prove that you know p and q by sending r or by computing s/r and sending that instead (if e=1), and your friend can verify that you know p and q or that s/r is a valid square root of s mod n without learning anything else about their values. This meets the conditions of completeness, soundness, and zero-knowledge.
Zero-knowledge proofs satisfy the following:
Completeness: The prover can demonstrate this to the verifier by computing q = n/p and sending both p and q to the verifier. The prover also knows a prime number p and a factorization of n as p*q.
Soundness: Since it is impossible to identify any pair of numbers that correctly factorize n without being aware of its prime factors, the prover is unable to demonstrate knowledge of any p and q that do not do so.
Zero knowledge: The prover only admits that they are aware of a prime number p and its associated factor q, which is already known to the verifier. This is the extent of their knowledge of the prime factors of n. As a result, the prover does not provide any new details regarding n's prime factors.
Types of Proofs of Zero Knowledge
Each zero-knowledge proof has pros and cons. Most zero-knowledge proofs are:
Interactive Zero Knowledge Proofs: The prover and the verifier work together to establish the proof in this sort of zero-knowledge proof. The verifier disputes the prover's assertions after receiving a sequence of messages from the prover. When the evidence has been established, the prover will employ these new problems to generate additional responses.
Non-Interactive Zero Knowledge Proofs: For this kind of zero-knowledge proof, the prover and verifier just need to exchange a single message. Without further interaction between the two parties, the proof is established.
A statistical zero-knowledge proof is one in which the conclusion is reached with a high degree of probability but not with certainty. This indicates that there is a remote possibility that the proof is false, but that this possibility is so remote as to be unimportant.
Succinct Non-Interactive Argument of Knowledge (SNARKs): SNARKs are an extremely effective and scalable form of zero-knowledge proof. They are utilized in many different applications, such as machine learning, blockchain technology, and more. Similar to other zero-knowledge proof techniques, SNARKs enable one party—the prover—to demonstrate to another—the verifier—that they are aware of a specific piece of information without disclosing any more information about that information.
The main characteristic of SNARKs is their succinctness, which refers to the fact that the size of the proof is substantially smaller than the amount of the original data being proved. Because to its high efficiency and scalability, SNARKs can be used in a wide range of applications, such as machine learning, blockchain technology, and more.
Uses for Zero Knowledge Proofs
ZKP applications include:
Verifying Identity ZKPs can be used to verify your identity without disclosing any personal information. This has uses in access control, digital signatures, and online authentication.
Proof of Ownership ZKPs can be used to demonstrate ownership of a certain asset without divulging any details about the asset itself. This has uses for protecting intellectual property, managing supply chains, and owning digital assets.
Financial Exchanges Without disclosing any details about the transaction itself, ZKPs can be used to validate financial transactions. Cryptocurrency, internet payments, and other digital financial transactions can all use this.
By enabling parties to make calculations on the data without disclosing the data itself, Data Privacy ZKPs can be used to preserve the privacy of sensitive data. Applications for this can be found in the financial, healthcare, and other sectors that handle sensitive data.
By enabling voters to confirm that their vote was counted without disclosing how they voted, elections ZKPs can be used to ensure the integrity of elections. This is applicable to electronic voting, including internet voting.
Cryptography Modern cryptography's ZKPs are a potent instrument that enable secure communication and authentication. This can be used for encrypted messaging and other purposes in the business sector as well as for military and intelligence operations.
Proofs of Zero Knowledge and Compliance
Kubernetes and regulatory compliance use ZKPs in many ways. Examples:
Security for Kubernetes ZKPs offer a mechanism to authenticate nodes without disclosing any sensitive information, enhancing the security of Kubernetes clusters. ZKPs, for instance, can be used to verify, without disclosing the specifics of the program, that the nodes in a Kubernetes cluster are running permitted software.
Compliance Inspection Without disclosing any sensitive information, ZKPs can be used to demonstrate compliance with rules like the GDPR, HIPAA, and PCI DSS. ZKPs, for instance, can be used to demonstrate that data has been encrypted and stored securely without divulging the specifics of the mechanism employed for either encryption or storage.
Access Management Without disclosing any private data, ZKPs can be used to offer safe access control to Kubernetes resources. ZKPs can be used, for instance, to demonstrate that a user has the necessary permissions to access a particular Kubernetes resource without disclosing the details of those permissions.
Safe Data Exchange Without disclosing any sensitive information, ZKPs can be used to securely transmit data between Kubernetes clusters or between several businesses. ZKPs, for instance, can be used to demonstrate the sharing of a specific piece of data between two parties without disclosing the details of the data itself.
Kubernetes deployments audited Without disclosing the specifics of the deployment or the data being processed, ZKPs can be used to demonstrate that Kubernetes deployments are working as planned. This can be helpful for auditing purposes and for ensuring that Kubernetes deployments are operating as planned.
ZKPs preserve data and maintain regulatory compliance by letting parties prove things without revealing sensitive information. ZKPs will be used more in Kubernetes as it grows.

Vitalik
4 years ago
An approximate introduction to how zk-SNARKs are possible (part 2)
If tasked with the problem of coming up with a zk-SNARK protocol, many people would make their way to this point and then get stuck and give up. How can a verifier possibly check every single piece of the computation, without looking at each piece of the computation individually? But it turns out that there is a clever solution.
Polynomials
Polynomials are a special class of algebraic expressions of the form:
- x+5
- x^4
- x^3+3x^2+3x+1
- 628x^{271}+318x^{270}+530x^{269}+…+69x+381
i.e. they are a sum of any (finite!) number of terms of the form cx^k
There are many things that are fascinating about polynomials. But here we are going to zoom in on a particular one: polynomials are a single mathematical object that can contain an unbounded amount of information (think of them as a list of integers and this is obvious). The fourth example above contained 816 digits of tau, and one can easily imagine a polynomial that contains far more.
Furthermore, a single equation between polynomials can represent an unbounded number of equations between numbers. For example, consider the equation A(x)+ B(x) = C(x). If this equation is true, then it's also true that:
- A(0)+B(0)=C(0)
- A(1)+B(1)=C(1)
- A(2)+B(2)=C(2)
- A(3)+B(3)=C(3)
And so on for every possible coordinate. You can even construct polynomials to deliberately represent sets of numbers so you can check many equations all at once. For example, suppose that you wanted to check:
- 12+1=13
- 10+8=18
- 15+8=23
- 15+13=28
You can use a procedure called Lagrange interpolation to construct polynomials A(x) that give (12,10,15,15) as outputs at some specific set of coordinates (eg. (0,1,2,3)), B(x) the outputs (1,8,8,13) on thos same coordinates, and so forth. In fact, here are the polynomials:
- A(x)=-2x^3+\frac{19}{2}x^2-\frac{19}{2}x+12
- B(x)=2x^3-\frac{19}{2}x^2+\frac{29}{2}x+1
- C(x)=5x+13
Checking the equation A(x)+B(x)=C(x) with these polynomials checks all four above equations at the same time.
Comparing a polynomial to itself
You can even check relationships between a large number of adjacent evaluations of the same polynomial using a simple polynomial equation. This is slightly more advanced. Suppose that you want to check that, for a given polynomial F, F(x+2)=F(x)+F(x+1) with the integer range {0,1…89} (so if you also check F(0)=F(1)=1, then F(100) would be the 100th Fibonacci number)
As polynomials, F(x+2)-F(x+1)-F(x) would not be exactly zero, as it could give arbitrary answers outside the range x={0,1…98}. But we can do something clever. In general, there is a rule that if a polynomial P is zero across some set S=\{x_1,x_2…x_n\} then it can be expressed as P(x)=Z(x)*H(x), where Z(x)=(x-x_1)*(x-x_2)*…*(x-x_n) and H(x) is also a polynomial. In other words, any polynomial that equals zero across some set is a (polynomial) multiple of the simplest (lowest-degree) polynomial that equals zero across that same set.
Why is this the case? It is a nice corollary of polynomial long division: the factor theorem. We know that, when dividing P(x) by Z(x), we will get a quotient Q(x) and a remainder R(x) is strictly less than that of Z(x). Since we know that P is zero on all of S, it means that R has to be zero on all of S as well. So we can simply compute R(x) via polynomial interpolation, since it's a polynomial of degree at most n-1 and we know n values (the zeros at S). Interpolating a polynomial with all zeroes gives the zero polynomial, thus R(x)=0 and H(x)=Q(x).
Going back to our example, if we have a polynomial F that encodes Fibonacci numbers (so F(x+2)=F(x)+F(x+1) across x=\{0,1…98\}), then I can convince you that F actually satisfies this condition by proving that the polynomial P(x)=F(x+2)-F(x+1)-F(x) is zero over that range, by giving you the quotient:
H(x)=\frac{F(x+2)-F(x+1)-F(x)}{Z(x)}
Where Z(x) = (x-0)*(x-1)*…*(x-98).
You can calculate Z(x) yourself (ideally you would have it precomputed), check the equation, and if the check passes then F(x) satisfies the condition!
Now, step back and notice what we did here. We converted a 100-step-long computation into a single equation with polynomials. Of course, proving the N'th Fibonacci number is not an especially useful task, especially since Fibonacci numbers have a closed form. But you can use exactly the same basic technique, just with some extra polynomials and some more complicated equations, to encode arbitrary computations with an arbitrarily large number of steps.
see part 3

Yusuf Ibrahim
4 years ago
How to sell 10,000 NFTs on OpenSea for FREE (Puppeteer/NodeJS)
So you've finished your NFT collection and are ready to sell it. Except you can't figure out how to mint them! Not sure about smart contracts or want to avoid rising gas prices. You've tried and failed with apps like Mini mouse macro, and you're not familiar with Selenium/Python. Worry no more, NodeJS and Puppeteer have arrived!
Learn how to automatically post and sell all 1000 of my AI-generated word NFTs (Nakahana) on OpenSea for FREE!
My NFT project — Nakahana |
NOTE: Only NFTs on the Polygon blockchain can be sold for free; Ethereum requires an initiation charge. NFTs can still be bought with (wrapped) ETH.
If you want to go right into the code, here's the GitHub link: https://github.com/Yusu-f/nftuploader
Let's start with the knowledge and tools you'll need.
What you should know
You must be able to write and run simple NodeJS programs. You must also know how to utilize a Metamask wallet.
Tools needed
- NodeJS. You'll need NodeJs to run the script and NPM to install the dependencies.
- Puppeteer – Use Puppeteer to automate your browser and go to sleep while your computer works.
- Metamask – Create a crypto wallet and sign transactions using Metamask (free). You may learn how to utilize Metamask here.
- Chrome – Puppeteer supports Chrome.
Let's get started now!
Starting Out
Clone Github Repo to your local machine. Make sure that NodeJS, Chrome, and Metamask are all installed and working. Navigate to the project folder and execute npm install. This installs all requirements.
Replace the “extension path” variable with the Metamask chrome extension path. Read this tutorial to find the path.
Substitute an array containing your NFT names and metadata for the “arr” variable and the “collection_name” variable with your collection’s name.
Run the script.
After that, run node nftuploader.js.
Open a new chrome instance (not chromium) and Metamask in it. Import your Opensea wallet using your Secret Recovery Phrase or create a new one and link it. The script will be unable to continue after this but don’t worry, it’s all part of the plan.
Next steps
Open your terminal again and copy the route that starts with “ws”, e.g. “ws:/localhost:53634/devtools/browser/c07cb303-c84d-430d-af06-dd599cf2a94f”. Replace the path in the connect function of the nftuploader.js script.
const browser = await puppeteer.connect({ browserWSEndpoint: "ws://localhost:58533/devtools/browser/d09307b4-7a75-40f6-8dff-07a71bfff9b3", defaultViewport: null });
Rerun node nftuploader.js. A second tab should open in THE SAME chrome instance, navigating to your Opensea collection. Your NFTs should now start uploading one after the other! If any errors occur, the NFTs and errors are logged in an errors.log file.
Error Handling
The errors.log file should show the name of the NFTs and the error type. The script has been changed to allow you to simply check if an NFT has already been posted. Simply set the “searchBeforeUpload” setting to true.
We're done!
If you liked it, you can buy one of my NFTs! If you have any concerns or would need a feature added, please let me know.
Thank you to everyone who has read and liked. I never expected it to be so popular.
You might also like

Jared A. Brock
3 years ago
Here is the actual reason why Russia invaded Ukraine
Democracy's demise
Our Ukrainian brothers and sisters are being attacked by a far superior force.
It's the biggest invasion since WWII.
43.3 million peaceful Ukrainians awoke this morning to tanks, mortars, and missiles. Russia is already 15 miles away.
America and the West will not deploy troops.
They're sanctioning. Except railways. And luxuries. And energy. Diamonds. Their dependence on Russian energy exports means they won't even cut Russia off from SWIFT.
Ukraine is desperate enough to hand out guns on the street.
France, Austria, Turkey, and the EU are considering military aid, but Ukraine will fall without America or NATO.
The Russian goal is likely to encircle Kyiv and topple Zelenskyy's government. A proxy power will be reinstated once Russia has total control.
“Western security services believe Putin intends to overthrow the government and install a puppet regime,” says Financial Times foreign affairs commentator Gideon Rachman. This “decapitation” strategy includes municipalities. Ukrainian officials are being targeted for arrest or death.”
Also, Putin has never lost a war.
Why is Russia attacking Ukraine?
Putin, like a snowflake college student, “feels unsafe.”
Why?
Because Ukraine is full of “Nazi ideas.”
Putin claims he has felt threatened by Ukraine since the country's pro-Putin leader was ousted and replaced by a popular Jewish comedian.
Hee hee
He fears a full-scale enemy on his doorstep if Ukraine joins NATO. But he refuses to see it both ways. NATO has never invaded Russia, but Russia has always stolen land from its neighbors. Can you blame them for joining a mutual defense alliance when a real threat exists?
Nations that feel threatened can join NATO. That doesn't justify an attack by Russia. It allows them to defend themselves. But NATO isn't attacking Moscow. They aren't.
Russian President Putin's "special operation" aims to de-Nazify the Jewish-led nation.
To keep Crimea and the other two regions he has already stolen, he wants Ukraine undefended by NATO.
(Warlords have fought for control of the strategically important Crimea for over 2,000 years.)
Putin wants to own all of Ukraine.
Why?
The Black Sea is his goal.
Ports bring money and power, and Ukraine pipelines transport Russian energy products.
Putin wants their wheat, too — with 70% crop coverage, Ukraine would be their southern breadbasket, and Russia has no qualms about starving millions of Ukrainians to death to feed its people.
In the end, it's all about greed and power.
Putin wants to own everything Russia has ever owned. This year he turns 70, and he wants to be remembered like his hero Peter the Great.
In order to get it, he's willing to kill thousands of Ukrainians
Art imitates life
This story began when a Jewish TV comedian portrayed a teacher elected President after ranting about corruption.
Servant of the People, the hit sitcom, is now the leading centrist political party.
Right, President Zelenskyy won the hearts and minds of Ukrainians by imagining a fairer world.
A fair fight is something dictators, corporatists, monopolists, and warlords despise.
Now Zelenskyy and his people will die, allowing one of history's most corrupt leaders to amass even more power.
The poor always lose
Meanwhile, the West will impose economic sanctions on Russia.
China is likely to step in to help Russia — or at least the wealthy.
The poor and working class in Russia will suffer greatly if there is a hard crash or long-term depression.
Putin's friends will continue to drink champagne and eat caviar.
Russia cutting off oil, gas, and fertilizer could cause more inflation and possibly a recession if it cuts off supplies to the West. This causes more suffering and hardship for the Western poor and working class.
Why? a billionaire sociopath gets his dirt.
Yes, Russia is simply copying America. Some of us think all war is morally wrong, regardless of who does it.
But let's not kid ourselves right now.
The markets rallied after the biggest invasion in Europe since WWII.
Investors hope Ukraine collapses and Russian oil flows.
Unbridled capitalists value lifeless.
What we can do about Ukraine
When the Russian army invaded eastern Finland, my wife's grandmother fled as a child. 80 years later, Russia still has Karelia.
Russia invaded Ukraine today to retake two eastern provinces.
History has taught us nothing.
Past mistakes won't fix the future.
Instead, we should try:
- Pray and/or meditate on our actions with our families.
- Stop buying Russian products (vodka, obviously, but also pay more for hydro/solar/geothermal/etc.)
- Stop wasting money on frivolous items and donate it to Ukrainian charities.
Here are 35+ places to donate.
- To protest, gather a few friends, contact the media, and shake signs in front of the Russian embassy.
- Prepare to welcome refugees.
More war won't save the planet or change hearts.
Only love can work.

Al Anany
3 years ago
Notion AI Might Destroy Grammarly and Jasper
The trick Notion could use is simply Facebook-ing the hell out of them.

*Time travel to fifteen years ago.* Future-Me: “Hey! What are you up to?” Old-Me: “I am proofreading an article. It’s taking a few hours, but I will be done soon.” Future-Me: “You know, in the future, you will be using a google chrome plugin called Grammarly that will help you easily proofread articles in half that time.” Old-Me: “What is… Google Chrome?” Future-Me: “Gosh…”
I love Grammarly. It’s one of those products that I personally feel the effects of. I mean, Space X is a great company. But I am not a rocket writing this article in space (or am I?)…
No, I’m not. So I don’t personally feel a connection to Space X. So, if a company collapse occurs in the morning, I might write about it. But I will have zero emotions regarding it.
Yet, if Grammarly fails tomorrow, I will feel 1% emotionally distressed. So looking at the title of this article, you’d realize that I am betting against them. This is how much I believe in the critical business model that’s taking over the world, the one of Notion.
Notion How frequently do you go through your notes?
Grammarly is everywhere, which helps its success. Grammarly is available when you update LinkedIn on Chrome. Grammarly prevents errors in Google Docs.
My internal concentration isn't apparent in the previous paragraph. Not Grammarly. I should have used Chrome to make a Google doc and LinkedIn update. Without this base, Grammarly will be useless.
So, welcome to this business essay.
Grammarly provides a solution.
Another issue is resolved by Jasper.
Your entire existence is supposed to be contained within Notion.
New Google Chrome is offline. It's an all-purpose notepad (in the near future.)
How should I start my blog? Enter it in Note.
an update on LinkedIn? If you mention it, it might be automatically uploaded there (with little help from another app.)
An advanced thesis? You can brainstorm it with your coworkers.
This ad sounds great! I won't cry if Notion dies tomorrow.
I'll reread the following passages to illustrate why I think Notion could kill Grammarly and Jasper.
Notion is a fantastic app that incubates your work.
Smartly, they began with note-taking.
Hopefully, your work will be on Notion. Grammarly and Jasper are still must-haves.
Grammarly will proofread your typing while Jasper helps with copywriting and AI picture development.
They're the best, therefore you'll need them. Correct? Nah.
Notion might bombard them with Facebook posts.
Notion: “Hi Grammarly, do you want to sell your product to us?” Grammarly: “Dude, we are more valuable than you are. We’ve even raised $400m, while you raised $342m. Our last valuation round put us at $13 billion, while yours put you at $10 billion. Go to hell.” Notion: “Okay, we’ll speak again in five years.”
Notion: “Jasper, wanna sell?” Jasper: “Nah, we’re deep into AI and the field. You can’t compete with our people.” Notion: “How about you either sell or you turn into a Snapchat case?” Jasper: “…”
Notion is your home. Grammarly is your neighbor. Your track is Jasper.
What if you grew enough vegetables in your backyard to avoid the supermarket? No more visits.
What if your home had a beautiful treadmill? You won't rush outside as much (I disagree with my own metaphor). (You get it.)
It's Facebooking. Instagram Stories reduced your Snapchat usage. Notion will reduce your need to use Grammarly.
The Final Piece of the AI Puzzle
Let's talk about Notion first, since you've probably read about it everywhere.
They raised $343 million, as I previously reported, and bought four businesses
According to Forbes, Notion will have more than 20 million users by 2022. The number of users is up from 4 million in 2020.
If raising $1.8 billion was impressive, FTX wouldn't have fallen.
This article compares the basic product to two others. Notion is a day-long app.
Notion has released Notion AI to support writers. It's early, so it's not as good as Jasper. Then-Jasper isn't now-Jasper. In five years, Notion AI will be different.
With hard work, they may construct a Jasper-like writing assistant. They have resources and users.
At this point, it's all speculation. Jasper's copywriting is top-notch. Grammarly's proofreading is top-notch. Businesses are constrained by user activities.
If Notion's future business movements are strategic, they might become a blue ocean shark (or get acquired by an unbelievable amount.)
I love business mental teasers, so tell me:
How do you feel? Are you a frequent Notion user?
Do you dispute my position? I enjoy hearing opposing viewpoints.
Ironically, I proofread this with Grammarly.

Christian Soschner
3 years ago
Steve Jobs' Secrets Revealed
From 1984 until 2011, he ran Apple using the same template.

What is a founder CEO's most crucial skill?
Presentation, communication, and sales
As a Business Angel Investor, I saw many pitch presentations and met with investors one-on-one to promote my companies.
There is always the conception of “Investors have to invest,” so there is no need to care about the presentation.
It's false. Nobody must invest. Many investors believe that entrepreneurs must convince them to invest in their business.
Sometimes — like in 2018–2022 — too much money enters the market, and everyone makes good money.
Do you recall the Buy Now, Pay Later Movement? This amazing narrative had no return potential. Only buyers who couldn't acquire financing elsewhere shopped at these companies.
Klarna's failing business concept led to high valuations.
Investors become more cautious when the economy falters. 2022 sees rising inflation, interest rates, wars, and civil instability. It's like the apocalypse's four horsemen have arrived.
Storytelling is important in rough economies.
When investors draw back, how can entrepreneurs stand out?
In Q2/2022, every study I've read said:
Investors cease investing
Deals are down in almost all IT industries from previous quarters.
What do founders need to do?
Differentiate yourself.
Storytelling talents help.
The Steve Jobs Way
Every time I watch a Steve Jobs presentation, I'm enthralled.
I'm a techie. Everything technical interests me. But, I skim most presentations.
What's Steve Jobs's secret?
Steve Jobs created Apple in 1976 and made it a profitable software and hardware firm in the 1980s. Macintosh goods couldn't beat IBM's. This mistake sacked him in 1985.
Before rejoining Apple in 1997, Steve Jobs founded Next Inc. and Pixar.
From then on, Apple became America's most valuable firm.
Steve Jobs understood people's needs. He said:
“People don’t know what they want until you show it to them. That’s why I never rely on market research. Our task is to read things that are not yet on the page.”
In his opinion, people talk about problems. A lot. Entrepreneurs must learn what the population's pressing problems are and create a solution.
Steve Jobs showed people what they needed before they realized it.
I'll explain:
Present a Big Vision
Steve Jobs starts every presentation by describing his long-term goals for Apple.
1984's Macintosh presentation set up David vs. Goliath. In a George Orwell-style dystopia, IBM computers were bad. It was 1984.
Apple will save the world, like Jedis.
Why do customers and investors like Big Vision?
People want a wider perspective, I think. Humans love improving the planet.
Apple users often cite emotional reasons for buying the brand.
Revolutionizing several industries with breakthrough inventions
Establish Authority
Everyone knows Apple in 2022. It's hard to find folks who confuse Apple with an apple around the world.
Apple wasn't as famous as it is today until Steve Jobs left in 2011.
Most entrepreneurs lack experience. They may market their company or items to folks who haven't heard of it.
Steve Jobs presented the company's historical accomplishments to overcome opposition.
In his presentation of the first iPhone, he talked about the Apple Macintosh, which altered the computing sector, and the iPod, which changed the music industry.
People who have never heard of Apple feel like they're seeing a winner. It raises expectations that the new product will be game-changing and must-have.
The Big Reveal
A pitch or product presentation always has something new.
Steve Jobs doesn't only demonstrate the product. I don't think he'd skip the major point of a company presentation.
He consistently discusses present market solutions, their faults, and a better consumer solution.
No solution exists yet.
It's a multi-faceted play:
It's comparing the new product to something familiar. This makes novelty and the product more relatable.
Describe a desirable solution.
He's funny. He demonstrated an iPod with an 80s phone dial in his iPhone presentation.
Then he reveals the new product. Macintosh presented itself.
Show the benefits
He outlines what Apple is doing differently after demonstrating the product.
How do you distinguish from others? The Big Breakthrough Presentation.
A few hundred slides might list all benefits.
Everyone would fall asleep. Have you ever had similar presentations?
When the brain is overloaded with knowledge, the limbic system changes to other duties, like lunch planning.
What should a speaker do? There's a classic proverb:
“Tell me and I forget, teach me and I may remember, involve me and I learn” (— Not Benjamin Franklin).
Steve Jobs showcased the product live.
Again, using ordinary scenarios to highlight the product's benefits makes it relatable.
The 2010 iPad Presentation uses this technique.
Invite the Team and Let Them Run the Presentation
CEOs spend most time outside the organization. Many companies elect to have only one presenter.
It sends the incorrect message to investors. Product presentations should always include the whole team.
Let me explain why.
Companies needing investment money frequently have shaky business strategies or no product-market fit or robust corporate structure.
Investors solely bet on a team's ability to implement ideas and make a profit.
Early team involvement helps investors understand the company's drivers. Travel costs are worthwhile.
But why for product presentations?
Presenters of varied ages, genders, social backgrounds, and skillsets are relatable. CEOs want relatable products.
Some customers may not believe a white man's message. A black woman's message may be more accepted.
Make the story relatable when you have the best product that solves people's concerns.
Best example: 1984 Macintosh presentation with development team panel.
What is the largest error people make when companies fail?
Saving money on the corporate and product presentation.
Invite your team to five partner meetings when five investors are shortlisted.
Rehearse the presentation till it's natural. Let the team speak.
Successful presentations require structure, rehearsal, and a team. Steve Jobs nailed it.
