More on Web3 & Crypto

Max Parasol
4 years ago
What the hell is Web3 anyway?
"Web 3.0" is a trendy buzzword with a vague definition. Everyone agrees it has to do with a blockchain-based internet evolution, but what is it?
Yet, the meaning and prospects for Web3 have become hot topics in crypto communities. Big corporations use the term to gain a foothold in the space while avoiding the negative connotations of “crypto.”
But it can't be evaluated without a definition.
Among those criticizing Web3's vagueness is Cobie:
“Despite the dominie's deluge of undistinguished think pieces, nobody really agrees on what Web3 is. Web3 is a scam, the future, tokenizing the world, VC exit liquidity, or just another name for crypto, depending on your tribe.
“Even the crypto community is split on whether Bitcoin is Web3,” he adds.
The phrase was coined by an early crypto thinker, and the community has had years to figure out what it means. Many ideologies and commercial realities have driven reverse engineering.
Web3 is becoming clearer as a concept. It contains ideas. It was probably coined by Ethereum co-founder Gavin Wood in 2014. His definition of Web3 included “trustless transactions” as part of its tech stack. Wood founded the Web3 Foundation and the Polkadot network, a Web3 alternative future.
The 2013 Ethereum white paper had previously allowed devotees to imagine a DAO, for example.
Web3 now has concepts like decentralized autonomous organizations, sovereign digital identity, censorship-free data storage, and data divided by multiple servers. They intertwine discussions about the “Web3” movement and its viability.
These ideas are linked by Cobie's initial Web3 definition. A key component of Web3 should be “ownership of value” for one's own content and data.
Noting that “late-stage capitalism greedcorps that make you buy a fractionalized micropayment NFT on Cardano to operate your electric toothbrush” may build the new web, he notes that “crypto founders are too rich to care anymore.”
Very Important
Many critics of Web3 claim it isn't practical or achievable. Web3 critics like Moxie Marlinspike (creator of sslstrip and Signal/TextSecure) can never see people running their own servers. Early in January, he argued that protocols are more difficult to create than platforms.
While this is true, some projects, like the file storage protocol IPFS, allow users to choose which jurisdictions their data is shared between.
But full decentralization is a difficult problem. Suhaza, replying to Moxie, said:
”People don't want to run servers... Companies are now offering API access to an Ethereum node as a service... Almost all DApps interact with the blockchain using Infura or Alchemy. In fact, when a DApp uses a wallet like MetaMask to interact with the blockchain, MetaMask is just calling Infura!
So, here are the questions: Web3: Is it a go? Is it truly decentralized?
Web3 history is shaped by Web2 failure.
This is the story of how the Internet was turned upside down...
Then came the vision. Everyone can create content for free. Decentralized open-source believers like Tim Berners-Lee popularized it.
Real-world data trade-offs for content creation and pricing.
A giant Wikipedia page married to a giant Craig's List. No ads, no logins, and a private web carve-up. For free usage, you give up your privacy and data to the algorithmic targeted advertising of Web 2.
Our data is centralized and savaged by giant corporations. Data localization rules and geopolitical walls like China's Great Firewall further fragment the internet.
The decentralized Web3 reflects Berners-original Lee's vision: "No permission is required from a central authority to post anything... there is no central controlling node and thus no single point of failure." Now he runs Solid, a Web3 data storage startup.
So Web3 starts with decentralized servers and data privacy.
Web3 begins with decentralized storage.
Data decentralization is a key feature of the Web3 tech stack. Web2 has closed databases. Large corporations like Facebook, Google, and others go to great lengths to collect, control, and monetize data. We want to change it.
Amazon, Google, Microsoft, Alibaba, and Huawei, according to Gartner, currently control 80% of the global cloud infrastructure market. Web3 wants to change that.
Decentralization enlarges power structures by giving participants a stake in the network. Users own data on open encrypted networks in Web3. This area has many projects.
Apps like Filecoin and IPFS have led the way. Data is replicated across multiple nodes in Web3 storage providers like Filecoin.
But the new tech stack and ideology raise many questions.
Giving users control over their data
According to Ryan Kris, COO of Verida, his “Web3 vision” is “empowering people to control their own data.”
Verida targets SDKs that address issues in the Web3 stack: identity, messaging, personal storage, and data interoperability.
A big app suite? “Yes, but it's a frontier technology,” he says. They are currently building a credentialing system for decentralized health in Bermuda.
By empowering individuals, how will Web3 create a fairer internet? Kris, who has worked in telecoms, finance, cyber security, and blockchain consulting for decades, admits it is difficult:
“The viability of Web3 raises some good business questions,” he adds. “How can users regain control over centralized personal data? How are startups motivated to build products and tools that support this transition? How are existing Web2 companies encouraged to pivot to a Web3 business model to compete with market leaders?
Kris adds that new technologies have regulatory and practical issues:
"On storage, IPFS is great for redundantly sharing public data, but not designed for securing private personal data. It is not controlled by the users. When data storage in a specific country is not guaranteed, regulatory issues arise."
Each project has varying degrees of decentralization. The diehards say DApps that use centralized storage are no longer “Web3” companies. But fully decentralized technology is hard to build.
Web2.5?
Some argue that we're actually building Web2.5 businesses, which are crypto-native but not fully decentralized. This is vital. For example, the NFT may be on a blockchain, but it is linked to centralized data repositories like OpenSea. A server failure could result in data loss.
However, according to Apollo Capital crypto analyst David Angliss, OpenSea is “not exactly community-led”. Also in 2021, much to the chagrin of crypto enthusiasts, OpenSea tried and failed to list on the Nasdaq.
This is where Web2.5 is defined.
“Web3 isn't a crypto segment. “Anything that uses a blockchain for censorship resistance is Web3,” Angliss tells us.
“Web3 gives users control over their data and identity. This is not possible in Web2.”
“Web2 is like feudalism, with walled-off ecosystems ruled by a few. For example, an honest user owned the Instagram account “Meta,” which Facebook rebranded and then had to make up a reason to suspend. Not anymore with Web3. If I buy ‘Ethereum.ens,' Ethereum cannot take it away from me.”
Angliss uses OpenSea as a Web2.5 business example. Too decentralized, i.e. censorship resistant, can be unprofitable for a large company like OpenSea. For example, OpenSea “enables NFT trading”. But it also stopped the sale of stolen Bored Apes.”
Web3 (or Web2.5, depending on the context) has been described as a new way to privatize internet.
“Being in the crypto ecosystem doesn't make it Web3,” Angliss says. The biggest risk is centralized closed ecosystems rather than a growing Web3.
LooksRare and OpenDAO are two community-led platforms that are more decentralized than OpenSea. LooksRare has even been “vampire attacking” OpenSea, indicating a Web3 competitor to the Web2.5 NFT king could find favor.
The addition of a token gives these new NFT platforms more options for building customer loyalty. For example, OpenSea charges a fee that goes nowhere. Stakeholders of LOOKS tokens earn 100% of the trading fees charged by LooksRare on every basic sale.
Maybe Web3's time has come.
So whose data is it?
Continuing criticisms of Web3 platforms' decentralization may indicate we're too early. Users want to own and store their in-game assets and NFTs on decentralized platforms like the Metaverse and play-to-earn games. Start-ups like Arweave, Sia, and Aleph.im propose an alternative.
To be truly decentralized, Web3 requires new off-chain models that sidestep cloud computing and Web2.5.
“Arweave and Sia emerged as formidable competitors this year,” says the Messari Report. They seek to reduce the risk of an NFT being lost due to a data breach on a centralized server.
Aleph.im, another Web3 cloud competitor, seeks to replace cloud computing with a service network. It is a decentralized computing network that supports multiple blockchains by retrieving and encrypting data.
“The Aleph.im network provides a truly decentralized alternative where it is most needed: storage and computing,” says Johnathan Schemoul, founder of Aleph.im. For reasons of consensus and security, blockchains are not designed for large storage or high-performance computing.
As a result, large data sets are frequently stored off-chain, increasing the risk for centralized databases like OpenSea
Aleph.im enables users to own digital assets using both blockchains and off-chain decentralized cloud technologies.
"We need to go beyond layer 0 and 1 to build a robust decentralized web. The Aleph.im ecosystem is proving that Web3 can be decentralized, and we intend to keep going.”
Aleph.im raised $10 million in mid-January 2022, and Ubisoft uses its network for NFT storage. This is the first time a big-budget gaming studio has given users this much control.
It also suggests Web3 could work as a B2B model, even if consumers aren't concerned about “decentralization.” Starting with gaming is common.
Can Tokenomics help Web3 adoption?
Web3 consumer adoption is another story. The average user may not be interested in all this decentralization talk. Still, how much do people value privacy over convenience? Can tokenomics solve the privacy vs. convenience dilemma?
Holon Global Investments' Jonathan Hooker tells us that human internet behavior will change. “Do you own Bitcoin?” he asks in his Web3 explanation. How does it feel to own and control your own sovereign wealth? Then:
“What if you could own and control your data like Bitcoin?”
“The business model must find what that person values,” he says. Putting their own health records on centralized systems they don't control?
“How vital are those medical records to that person at a critical time anywhere in the world? Filecoin and IPFS can help.”
Web3 adoption depends on NFT storage competition. A free off-chain storage of NFT metadata and assets was launched by Filecoin in April 2021.
Denationalization and blockchain technology have significant implications for data ownership and compensation for lending, staking, and using data.
Tokenomics can change human behavior, but many people simply sign into Web2 apps using a Facebook API without hesitation. Our data is already owned by Google, Baidu, Tencent, and Facebook (and its parent company Meta). Is it too late to recover?
Maybe. “Data is like fruit, it starts out fresh but ages,” he says. "Big Tech's data on us will expire."
Web3 founder Kris agrees with Hooker that “value for data is the issue, not privacy.” People accept losing their data privacy, so tokenize it. People readily give up data, so why not pay for it?
"Personalized data offering is valuable in personalization. “I will sell my social media data but not my health data.”
Purists and mass consumer adoption struggle with key management.
Others question data tokenomics' optimism. While acknowledging its potential, Box founder Aaron Levie questioned the viability of Web3 models in a Tweet thread:
“Why? Because data almost always works in an app. A product and APIs that moved quickly to build value and trust over time.”
Levie contends that tokenomics may complicate matters. In addition to community governance and tokenomics, Web3 ideals likely add a new negotiation vector.
“These are hard problems about human coordination, not software or blockchains,”. Using a Facebook API is simple. The business model and user interface are crucial.
For example, the crypto faithful have a common misconception about logging into Web3. It goes like this: Web 1 had usernames and passwords. Web 2 uses Google, Facebook, or Twitter APIs, while Web 3 uses your wallet. Pay with Ethereum on MetaMask, for example.
But Levie is correct. Blockchain key management is stressed in this meme. Even seasoned crypto enthusiasts have heart attacks, let alone newbies.
Web3 requires a better user experience, according to Kris, the company's founder. “How does a user recover keys?”
And at this point, no solution is likely to be completely decentralized. So Web3 key management can be improved. ”The moment someone loses control of their keys, Web3 ceases to exist.”
That leaves a major issue for Web3 purists. Put this one in the too-hard basket.
Is 2022 the Year of Web3?
Web3 must first solve a number of issues before it can be mainstreamed. It must be better and cheaper than Web2.5, or have other significant advantages.
Web3 aims for scalability without sacrificing decentralization protocols. But decentralization is difficult and centralized services are more convenient.
Ethereum co-founder Vitalik Buterin himself stated recently"
This is why (centralized) Binance to Binance transactions trump Ethereum payments in some places because they don't have to be verified 12 times."
“I do think a lot of people care about decentralization, but they're not going to take decentralization if decentralization costs $8 per transaction,” he continued.
“Blockchains need to be affordable for people to use them in mainstream applications... Not for 2014 whales, but for today's users."
For now, scalability, tokenomics, mainstream adoption, and decentralization believers seem to be holding Web3 hostage.
Much like crypto's past.
But stay tuned.

CyberPunkMetalHead
3 years ago
It's all about the ego with Terra 2.0.
UST depegs and LUNA crashes 99.999% in a fraction of the time it takes the Moon to orbit the Earth.
Fat Man, a Terra whistle-blower, promises to expose Do Kwon's dirty secrets and shady deals.

The Terra community has voted to relaunch Terra LUNA on a new blockchain. The Terra 2.0 Pheonix-1 blockchain went live on May 28, 2022, and people were airdropped the new LUNA, now called LUNA, while the old LUNA became LUNA Classic.
Does LUNA deserve another chance? To answer this, or at least start a conversation about the Terra 2.0 chain's advantages and limitations, we must assess its fundamentals, ideology, and long-term vision.
Whatever the result, our analysis must be thorough and ruthless. A failure of this magnitude cannot happen again, so we must magnify every potential breaking point by 10.
Will UST and LUNA holders be compensated in full?
The obvious. First, and arguably most important, is to restore previous UST and LUNA holders' bags.
Terra 2.0 has 1,000,000,000,000 tokens to distribute.
25% of a community pool
Holders of pre-attack LUNA: 35%
10% of aUST holders prior to attack
Holders of LUNA after an attack: 10%
UST holders as of the attack: 20%
Every LUNA and UST holder has been compensated according to the above proposal.
According to self-reported data, the new chain has 210.000.000 tokens and a $1.3bn marketcap. LUNC and UST alone lost $40bn. The new token must fill this gap. Since launch:
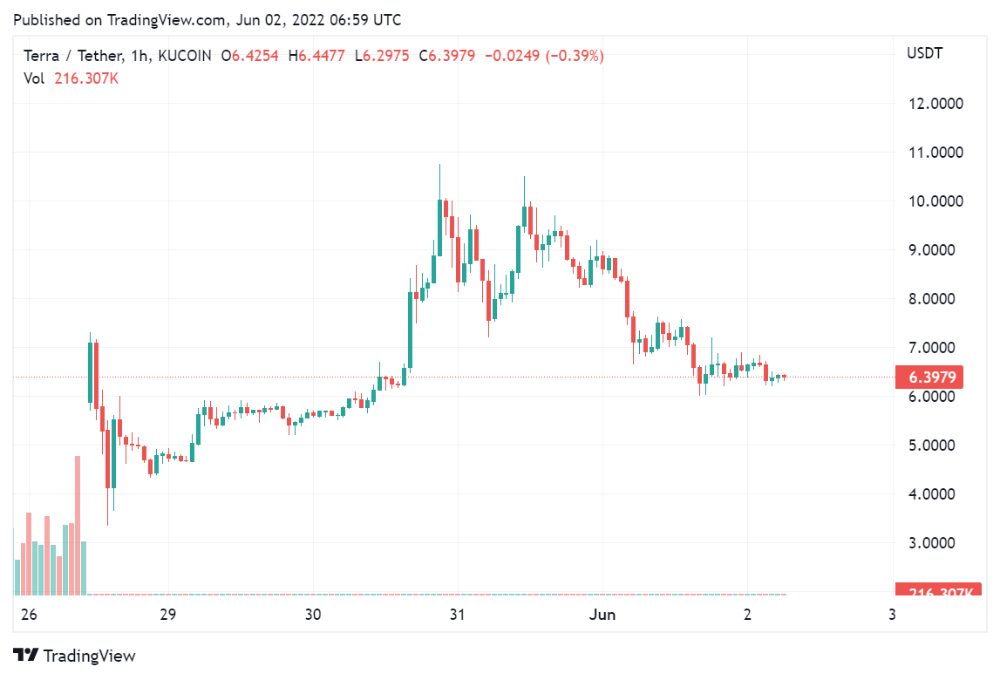
LUNA holders collectively own $1b worth of LUNA if we subtract the 25% community pool airdrop from the current market cap and assume airdropped LUNA was never sold.
At the current supply, the chain must grow 40 times to compensate holders. At the current supply, LUNA must reach $240.
LUNA needs a full-on Bull Market to make LUNC and UST holders whole.
Who knows if you'll be whole? From the time you bought to the amount and price, there are too many variables to determine if Terra can cover individual losses.
The above distribution doesn't consider individual cases. Terra didn't solve individual cases. It would have been huge.
What does LUNA offer in terms of value?
UST's marketcap peaked at $18bn, while LUNC's was $41bn. LUNC and UST drove the Terra chain's value.
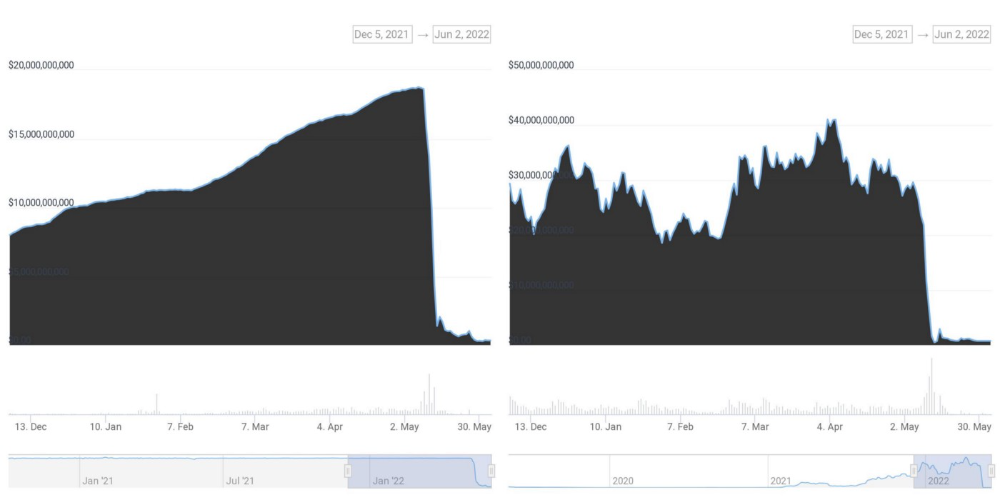
After it was confirmed (again) that algorithmic stablecoins are bad, Terra 2.0 will no longer support them.
Algorithmic stablecoins contributed greatly to Terra's growth and value proposition. Terra 2.0 has no product without algorithmic stablecoins.
Terra 2.0 has an identity crisis because it has no actual product. It's like Volkswagen faking carbon emission results and then stopping car production.
A project that has already lost the trust of its users and nearly all of its value cannot survive without a clear and in-demand use case.
Do Kwon, how about him?
Oh, the Twitter-caller-poor? Who challenges crypto billionaires to break his LUNA chain? Who dissolved Terra Labs South Korea before depeg? Arrogant guy?
That's not a good image for LUNA, especially when making amends. I think he should step down and let a nicer person be Terra 2.0's frontman.
The verdict
Terra has a terrific community with an arrogant, unlikeable leader. The new LUNA chain must grow 40 times before it can start making up its losses, and even then, not everyone's losses will be covered.
I won't invest in Terra 2.0 or other algorithmic stablecoins in the near future. I won't be near any Do Kwon-related project within 100 miles. My opinion.
Can Terra 2.0 be saved? Comment below.

Jeff Scallop
3 years ago
The Age of Decentralized Capitalism and DeFi
DeCap is DeFi's killer app.

“Software is eating the world.” Marc Andreesen, venture capitalist
DeFi. Imagine a blockchain-based alternative financial system that offers the same products and services as traditional finance, but with more variety, faster, more secure, lower cost, and simpler access.
Decentralised finance (DeFi) is a marketplace without gatekeepers or central authority managing the flow of money, where customers engage directly with smart contracts running on a blockchain.
DeFi grew exponentially in 2020/21, with Total Value Locked (an inadequate estimate for market size) topping at $100 billion. After that, it crashed.
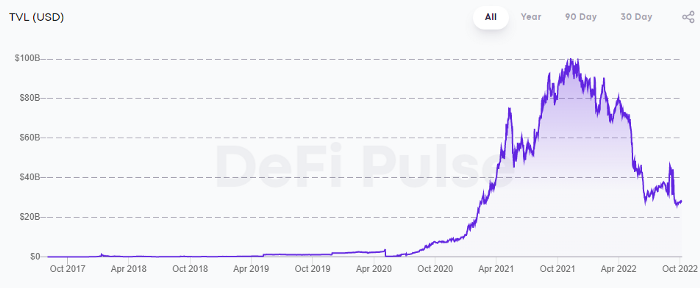
The accumulation of funds by individuals with high discretionary income during the epidemic, the novelty of crypto trading, and the high yields given (5% APY for stablecoins on established platforms to 100%+ for risky assets) are among the primary elements explaining this exponential increase.
No longer your older brothers DeFi
Since transactions are anonymous, borrowers had to overcollateralize DeFi 1.0. To borrow $100 in stablecoins, you must deposit $150 in ETH. DeFi 1.0's business strategy raises two problems.
Why does DeFi offer interest rates that are higher than those of the conventional financial system?;
Why would somebody put down more cash than they intended to borrow?
Maxed out on their own resources, investors took loans to acquire more crypto; the demand for those loans raised DeFi yields, which kept crypto prices increasing; as crypto prices rose, investors made a return on their positions, allowing them to deposit more money and borrow more crypto.
This is a bull market game. DeFi 1.0's overcollateralization speculation is dead. Cryptocrash sank it.
The “speculation by overcollateralisation” world of DeFi 1.0 is dead
At a JP Morgan digital assets conference, institutional investors were more interested in DeFi than crypto or fintech. To me, that shows DeFi 2.0's institutional future.
DeFi 2.0 protocols must handle KYC/AML, tax compliance, market abuse, and cybersecurity problems to be institutional-ready.
Stablecoins gaining market share under benign regulation and more CBDCs coming online in the next couple of years could help DeFi 2.0 separate from crypto volatility.
DeFi 2.0 will have a better footing to finally decouple from crypto volatility
Then we can transition from speculation through overcollateralization to DeFi's genuine comparative advantages: cheaper transaction costs, near-instant settlement, more efficient price discovery, faster time-to-market for financial innovation, and a superior audit trail.
Akin to Amazon for financial goods
Amazon decimated brick-and-mortar shops by offering millions of things online, warehouses by keeping just-in-time inventory, and back-offices by automating invoicing and payments. Software devoured retail. DeFi will eat banking with software.
DeFi is the Amazon for financial items that will replace fintech. Even the most advanced internet brokers offer only 100 currency pairings and limited bonds, equities, and ETFs.
Old banks settlement systems and inefficient, hard-to-upgrade outdated software harm them. For advanced gamers, it's like driving an F1 vehicle on dirt.
It is like driving a F1 car on a dirt road, for the most sophisticated players
Central bankers throughout the world know how expensive and difficult it is to handle cross-border payments using the US dollar as the reserve currency, which is vulnerable to the economic cycle and geopolitical tensions.
Decentralization is the only method to deliver 24h global financial markets. DeFi 2.0 lets you buy and sell startup shares like Google or Tesla. VC funds will trade like mutual funds. Or create a bundle coverage for your car, house, and NFTs. Defi 2.0 consumes banking and creates Global Wall Street.
Defi 2.0 is how software eats banking and delivers the global Wall Street
Decentralized Capitalism is Emerging
90% of markets are digital. 10% is hardest to digitalize. That's money creation, ID, and asset tokenization.
90% of financial markets are already digital. The only problem is that the 10% left is the hardest to digitalize
Debt helped Athens construct a powerful navy that secured trade routes. Bonds financed the Renaissance's wars and supply chains. Equity fueled industrial growth. FX drove globalization's payments system. DeFi's plans:
If the 20th century was a conflict between governments and markets over economic drivers, the 21st century will be between centralized and decentralized corporate structures.
Offices vs. telecommuting. China vs. onshoring/friendshoring. Oil & gas vs. diverse energy matrix. National vs. multilateral policymaking. DAOs vs. corporations Fiat vs. crypto. TradFi vs.
An age where the network effects of the sharing economy will overtake the gains of scale of the monopolistic competition economy
This is the dawn of Decentralized Capitalism (or DeCap), an age where the network effects of the sharing economy will reach a tipping point and surpass the scale gains of the monopolistic competition economy, further eliminating inefficiencies and creating a more robust economy through better data and automation. DeFi 2.0 enables this.
DeFi needs to pay the piper now.
DeCap won't be Web3.0's Shangri-La, though. That's too much for an ailing Atlas. When push comes to shove, DeFi folks want to survive and fight another day for the revolution. If feasible, make a tidy profit.
Decentralization wasn't meant to circumvent regulation. It circumvents censorship. On-ramp, off-ramp measures (control DeFi's entry and exit points, not what happens in between) sound like a good compromise for DeFi 2.0.
The sooner authorities realize that DeFi regulation is made ex-ante by writing code and constructing smart contracts with rules, the faster DeFi 2.0 will become the more efficient and safe financial marketplace.
More crucially, we must boost system liquidity. DeFi's financial stability risks are downplayed. DeFi must improve its liquidity management if it's to become mainstream, just as banks rely on capital constraints.
This reveals the complex and, frankly, inadequate governance arrangements for DeFi protocols. They redistribute control from tokenholders to developers, which is bad governance regardless of the economic model.
But crypto can only ride the existing banking system for so long before forming its own economy. DeFi will upgrade web2.0's financial rails till then.
You might also like

Francesca Furchtgott
3 years ago
Giving customers what they want or betraying the values of the brand?
A J.Crew collaboration for fashion label Eveliina Vintage is not a paradox; it is a solution.

Eveliina Vintage's capsule collection debuted yesterday at J.Crew. This J.Crew partnership stopped me in my tracks.
Eveliina Vintage sells vintage goods. Eeva Musacchia founded the shop in Finland in the 1970s. It's recognized for its one-of-a-kind slip dresses from the 1930s and 1940s.
I wondered why a vintage brand would partner with a mass shop. Fast fashion against vintage shopping? Will Eveliina Vintages customers be turned off?
But Eveliina Vintages customers don't care about sustainability. They want Eveliina's Instagram look. Eveliina Vintage collaborated with J.Crew to give customers what they wanted: more Eveliina at a lower price.
Vintage: A Fashion Option That Is Eco-Conscious
Secondhand shopping is a trendy response to quick fashion. J.Crew releases hundreds of styles annually. Waste and environmental damage have been criticized. A pair of jeans requires 1,800 gallons of water. J.Crew's limited-time deals promote more purchases. J.Crew items are likely among those Americans wear 7 times before discarding.
Consumers and designers have emphasized sustainability in recent years. Stella McCartney and Eileen Fisher are popular eco-friendly brands. They've also flocked to ThredUp and similar sites.
Gap, Levis, and Allbirds have listened to consumer requests. They promote recycling, ethical sourcing, and secondhand shopping.
Secondhand shoppers feel good about reusing and recycling clothing that might have ended up in a landfill.
Eco-conscious fashionistas shop vintage. These shoppers enjoy the thrill of the hunt (that limited-edition Chanel bag!) and showing off a unique piece (nobody will have my look!). They also reduce their environmental impact.
Is Eveliina Vintage capitalizing on an aesthetic or is it a sustainable brand?
Eveliina Vintage emphasizes environmental responsibility. Vogue's Amanda Musacchia emphasized sustainability. Amanda, founder Eeva's daughter, is a company leader.
But Eveliina's press message doesn't address sustainability, unlike Instagram. Scarcity and fame rule.
Eveliina Vintages Instagram has see-through dresses and lace-trimmed slip dresses. Celebrities and influencers are often photographed in Eveliina's apparel, which has 53,000+ followers. Vogue appreciates Eveliina's style. Multiple publications discuss Alexa Chung's Eveliina dress.
Eveliina Vintage markets its one-of-a-kind goods. It teases future content, encouraging visitors to return. Scarcity drives demand and raises clothing prices. One dress is $1,600+, but most are $500-$1,000.
The catch: Eveliina can't monetize its expanding popularity due to exorbitant prices and limited quantity. Why?
Most people struggle to pay for their clothing. But Eveliina Vintage lacks those more affordable entry-level products, in contrast to other luxury labels that sell accessories or perfume.
Many people have trouble fitting into their clothing. The bodies of most women in the past were different from those for which vintage clothing was designed. Each Eveliina dress's specific measurements are mentioned alongside it. Be careful, you can fall in love with an ill-fitting dress.
No matter how many people can afford it and fit into it, there is only one item to sell. To get the item before someone else does, those people must be on the Eveliina Vintage website as soon as it becomes available.
A Way for Eveliina Vintage to Make Money (and Expand) with J.Crew Its following
Eveliina Vintages' cooperation with J.Crew makes commercial sense.
This partnership spreads Eveliina's style. Slightly better pricing The $390 outfits have multicolored slips and gauzy cotton gowns. Sizes range from 00 to 24, which is wider than vintage racks.
Eveliina Vintage customers like the combination. Excited comments flood the brand's Instagram launch post. Nobody is mocking the 50-year-old vintage brand's fast-fashion partnership.
Vintage may be a sustainable fashion trend, but that's not why Eveliina's clients love the brand. They only care about the old look.
And that is a tale as old as fashion.

ANTHONY P.
3 years ago
Startups are difficult. Streamlining the procedure for creating the following unicorn.
New ventures are exciting. It's fun to imagine yourself rich, successful, and famous (if that's your thing). How you'll help others and make your family proud. This excitement can pull you forward for years, even when you intuitively realize that the path you're on may not lead to your desired success.
Know when to change course. Switching course can mean pivoting or changing direction.
In this not-so-short blog, I'll describe the journey of building your dream. And how the journey might look when you think you're building your dream, but fall short of that vision. Both can feel similar in the beginning, but there are subtle differences.
Let’s dive in.
How an exciting journey to a dead end looks and feels.
You want to help many people. You're business-minded, creative, and ambitious. You jump into entrepreneurship. You're excited, free, and in control.
I'll use tech as an example because that's what I know best, but this applies to any entrepreneurial endeavor.
So you start learning the basics of your field, say coding/software development. You read books, take courses, and may even join a bootcamp. You start practicing, and the journey begins. Once you reach a certain level of skill (which can take months, usually 12-24), you gain the confidence to speak with others in the field and find common ground. You might attract a co-founder this way with time. You and this person embark on a journey (Tip: the idea you start with is rarely the idea you end with).
Amateur mistake #1: You spend months building a product before speaking to customers.
Building something pulls you forward blindly. You make mistakes, avoid customers, and build with your co-founder or small team in the dark for months, usually 6-12 months.
You're excited when the product launches. We'll be billionaires! The market won't believe it. This excites you and the team. Launch.
….
Nothing happens.
Some people may sign up out of pity, only to never use the product or service again.
You and the team are confused, discouraged and in denial. They don't get what we've built yet. We need to market it better, we need to talk to more investors, someone will understand our vision.
This is a hopeless path, and your denial could last another 6 months. If you're lucky, while talking to consumers and investors (which you should have done from the start), someone who has been there before would pity you and give you an idea to pivot into that can create income.
Suppose you get this idea and pivot your business. Again, you've just pivoted into something limited by what you've already built. It may be a revenue-generating idea, but it's rarely new. Now you're playing catch-up, doing something others are doing but you can do better. (Tip #2: Don't be late.) Your chances of winning are slim, and you'll likely never catch up.
You're finally seeing revenue and feel successful. You can compete, but if you're not a first mover, you won't earn enough over time. You'll get by or work harder than ever to earn what a skilled trade could provide. You didn't go into business to stress out and make $100,000 or $200,000 a year. When you can make the same amount by becoming a great software developer, electrician, etc.
You become stuck. Either your firm continues this way for years until you realize there isn't enough growth to recruit a strong team and remove yourself from day-to-day operations due to competition. Or a catastrophic economic event forces you to admit that what you were building wasn't new and unique and wouldn't get you where you wanted to be.
This realization could take 6-10 years. No kidding.
The good news is, you’ve learned a lot along the way and this information can be used towards your next venture (if you have the energy).
Key Lesson: Don’t build something if you aren’t one of the first in the space building it just for the sake of building something.
-
Let's discuss what it's like to build something that can make your dream come true.
Case 2: Building something the market loves is difficult but rewarding.
It starts with a problem that hasn't been adequately solved for a long time but is now solvable due to technology. Or a new problem due to a change in how things are done.
Let's examine each example.
Example #1: Mass communication. The problem is now solvable due to some technological breakthrough.
Twitter — One of the first web 2 companies that became successful with the rise of smart mobile computing.
People can share their real-time activities via mobile device with friends, family, and strangers. Web 2 and smartphones made it easy and fun.
Example #2: A new problem has emerged due to some change in the way things are conducted.
Zoom- A web-conferencing company that reached massive success due to the movement towards “work from home”, remote/hybrid work forces.
Online web conferencing allows for face-to-face communication.
-
These two examples show how to build a unicorn-type company. It's a mix of solving the right problem at the right time, either through a technological breakthrough that opens up new opportunities or by fundamentally changing how people do things.
Let's find these opportunities.
Start by examining problems, such as how the world has changed and how we can help it adapt. It can also be both. Start team brainstorming. Research technologies, current world-trends, use common sense, and make a list. Then, choose the top 3 that you're most excited about and seem most workable based on your skillsets, values, and passion.
Once you have this list, create the simplest MVP you can and test it with customers. The prototype can be as simple as a picture or diagram of user flow and end-user value. No coding required. Market-test. Twitter's version 1 was simple. It was a web form that asked, "What are you doing?" Then publish it from your phone. A global status update, wherever you are. Currently, this company has a $50 billion market cap.
Here's their MVP screenshot.
Small things grow. Tiny. Simplify.
Remember Frequency and Value when brainstorming. Your product is high frequency (Twitter, Instagram, Snapchat, TikTok) or high value (Airbnb for renting travel accommodations), or both (Gmail).
Once you've identified product ideas that meet the above criteria, they're simple, have a high frequency of use, or provide deep value. You then bring it to market in the simplest, most cost-effective way. You can sell a half-working prototype with imagination and sales skills. You need just enough of a prototype to convey your vision to a user or customer.
With this, you can approach real people. This will do one of three things: give you a green light to continue on your vision as is, show you that there is no opportunity and people won't use it, or point you in a direction that is a blend of what you've come up with and what the customer / user really wants, and you update the prototype and go back to the maze. Repeat until you have enough yeses and conviction to build an MVP.
Tom Connor
3 years ago
12 mental models that I use frequently
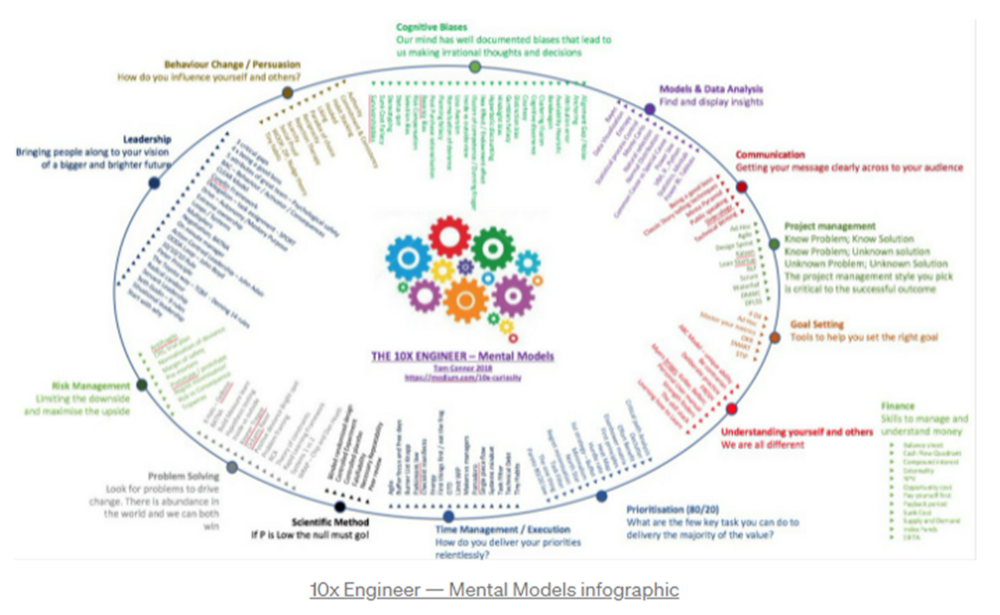
https://tomconnor.me/wp-content/uploads/2021/08/10x-Engineer-Mental-Models.pdf
I keep returning to the same mental models and tricks after writing and reading about a wide range of topics.
Top 12 mental models
12.
Survival bias - We perceive the surviving population as remarkable, yet they may have gotten there through sheer grit.
Survivorship bias affects us in many situations. Our retirement fund; the unicorn business; the winning team. We often study and imitate the last one standing. This can lead to genuine insights and performance improvements, but it can also lead us astray because the leader may just be lucky.
11.
The Helsinki Bus Theory - How to persevere Buss up!
Always display new work, and always be compared to others. Why? Easy. Keep riding. Stay on the fucking bus.
10.
Until it sticks… Turning up every day… — Artists teach engineers plenty. Quality work over a career comes from showing up every day and starting.
9.
WRAP decision making process (Heath Brothers)
Decision-making WRAP Model:
W — Widen your Options
R — Reality test your assumptions
A — Attain Distance
P — Prepare to be wrong or Right
8.
Systems for knowledge worker excellence - Todd Henry and Cal Newport write about techniques knowledge workers can employ to build a creative rhythm and do better work.
Todd Henry's FRESH framework:
Focus: Keep the start in mind as you wrap up.
Relationships: close a loop that's open.
Pruning is an energy.
Set aside time to be inspired by stimuli.
Hours: Spend time thinking.
7.
BBT is learning from mistakes. Science has transformed the world because it constantly updates its theories in light of failures. Complexity guarantees failure. Do we learn or self-justify?
6.
The OODA Loop - Competitive advantage
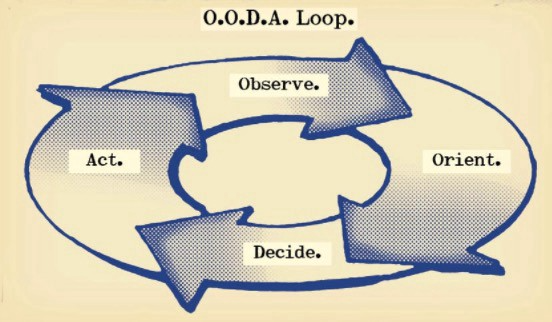
O: Observe: collect the data. Figure out exactly where you are, what’s happening.
O: Orient: analyze/synthesize the data to form an accurate picture.
D: Decide: select an action from possible options
A: Action: execute the action, and return to step (1)
Boyd's approach indicates that speed and agility are about information processing, not physical reactions. They form feedback loops. More OODA loops improve speed.
5.
Leaders who try to impose order in a complex situation fail; those who set the stage, step back, and allow patterns to develop win.
https://vimeo.com/640941172?embedded=true&source=vimeo_logo&owner=11999906
4.
Information Gap - The discrepancy between what we know and what we would like to know
Gap in Alignment - What individuals actually do as opposed to what we wish them to do
Effects Gap - the discrepancy between our expectations and the results of our actions
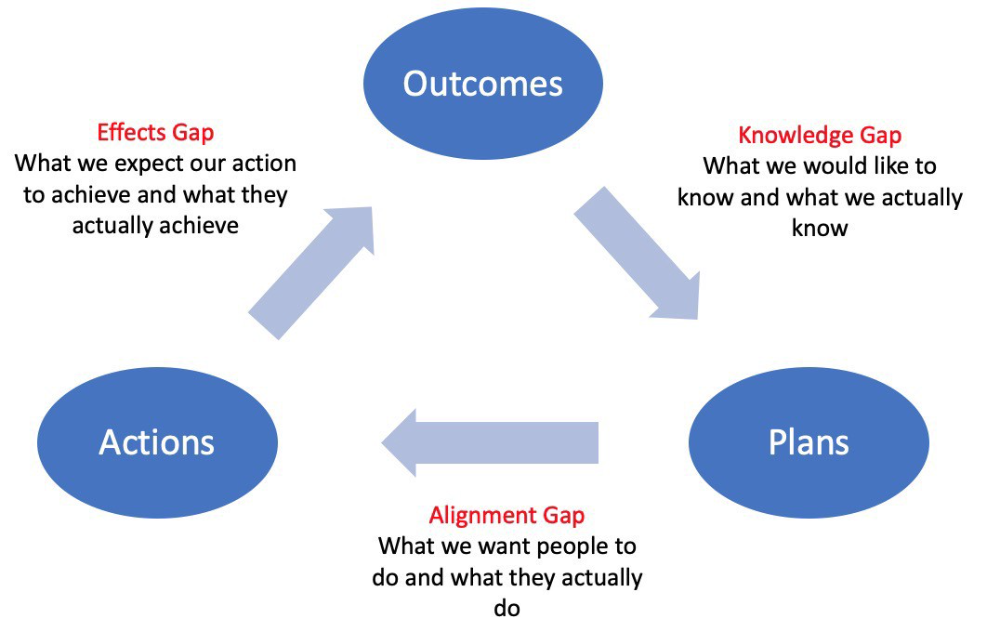
3.
Theory of Constraints — The Goal - To maximize system production, maximize bottleneck throughput.
Goldratt creates a five-step procedure:
Determine the restriction
Improve the restriction.
Everything else should be based on the limitation.
Increase the restriction
Go back to step 1 Avoid letting inertia become a limitation.
Any non-constraint improvement is an illusion.
2.
Serendipity and the Adjacent Possible - Why do several amazing ideas emerge at once? How can you foster serendipity in your work?
You need specialized abilities to reach to the edge of possibilities, where you can pursue exciting tasks that will change the world. Few people do it since it takes a lot of hard work. You'll stand out if you do.
Most people simply lack the comfort with discomfort required to tackle really hard things. At some point, in other words, there’s no way getting around the necessity to clear your calendar, shut down your phone, and spend several hard days trying to make sense of the damn proof.
1.
Boundaries of failure - Rasmussen's accident model.

Rasmussen modeled this. It has economic, workload, and performance boundaries.
The economic boundary is a company's profit zone. If the lights are on, you're within the economic boundaries, but there's pressure to cut costs and do more.
Performance limit reflects system capacity. Taking shortcuts is a human desire to minimize work. This is often necessary to survive because there's always more labor.
Both push operating points toward acceptable performance. Personal or process safety, or equipment performance.
If you exceed acceptable performance, you'll push back, typically forcefully.