More on Technology

Nikhil Vemu
3 years ago
7 Mac Apps That Are Exorbitantly Priced But Totally Worth It

Wish you more bang for your buck
By ‘Cost a Bomb’ I didn’t mean to exaggerate. It’s an idiom that means ‘To be very expensive’. In fact, no app on the planet costs a bomb lol.
So, to the point.
Chronicle
(Freemium. For Pro, $24.99 | Available on Setapp)
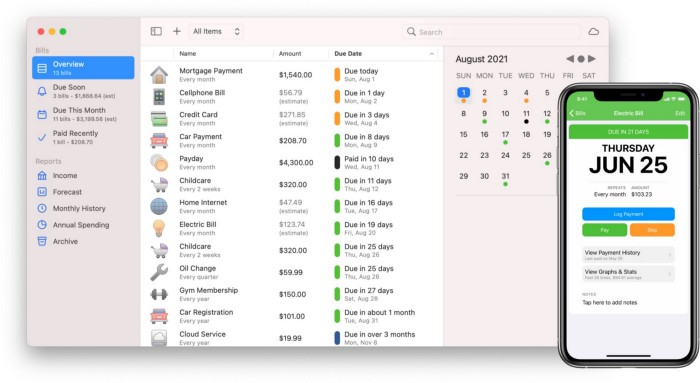
You probably have trouble keeping track of dozens of bills and subscriptions each month.
Try Chronicle.
Easy-to-use app
Add payment due dates and receive reminders,
Save payment documentation,
Analyze your spending by season, year, and month.
Observe expenditure trends and create new budgets.
Best of all, Chronicle features an integrated browser for fast payment and logging.
iOS and macOS sync.
SoundSource
($39 for lifetime)
Background Music, a free macOS program, was featured in #6 of this post last month.
It controls per-app volume, stereo balance, and audio over its max level.
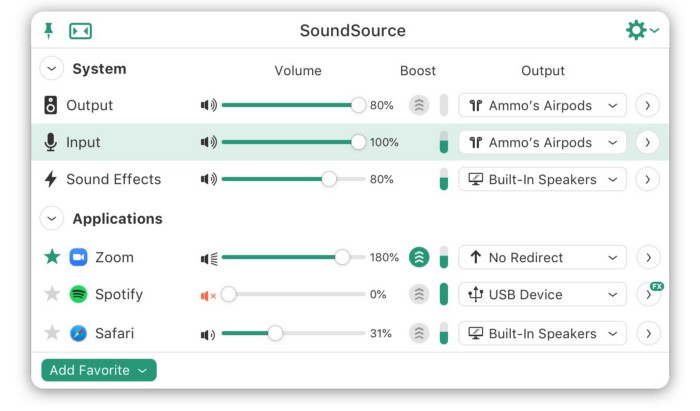
Background Music is fully supported. Additionally,
Connect various speakers to various apps (Wow! ),
change the audio sample rate for each app,
To facilitate access, add a floating SoundSource window.
Use its blocks in Shortcuts app,
On the menu bar, include meters for output/input devices and running programs.
PixelSnap
($39 for lifetime | Available on Setapp)
This software is heaven for UI designers.
It aids you.
quickly calculate screen distances (in pixels) ,
Drag an area around an object to determine its borders,

Measure the distances between the additional guides,

screenshots should be pixel-perfect.
What’s more.
You can
Adapt your tolerance for items with poor contrast and shadows.
Use your Touch Bar to perform important tasks, if you have one.
Mate Translation
($3.99 a month / $29.99 a year | Available on Setapp)
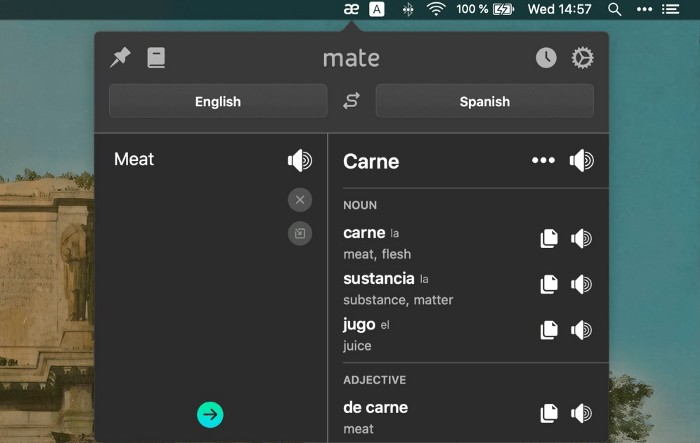
Mate Translate resembles a roided-up version of BarTranslate, which I wrote about in #1 of this piece last month.
If you translate often, utilize Mate Translate on macOS and Safari.
I'm really vocal about it.
It stays on the menu bar, and is accessible with a click or ⌥+shift+T hotkey.
It lets you
Translate in 103 different languages,
To translate text, double-click or right-click on it.
Totally translate websites. Additionally, Netflix subtitles,
Listen to their pronunciation to see how close it is to human.
iPhone and Mac sync Mate-ing history.
Swish
($16 for lifetime | Available on Setapp)
Swish is awesome!
Swipe, squeeze, tap, and hold movements organize chaotic desktop windows. Swish operates with mouse and trackpad.
Some gestures:
• Pinch Once: Close an app
• Pinch Twice: Quit an app
• Swipe down once: Minimise an app
• Pinch Out: Enter fullscreen mode
• Tap, Hold, & Swipe: Arrange apps in grids
and many more...

After getting acquainted to the movements, your multitasking will improve.
Unite
($24.99 for lifetime | Available on Setapp)
It turns webapps into macOS apps. The end.
Unite's functionality is a million times better.

Provide extensive customization (incl. its icon, light and dark modes)
make menu bar applications,
Get badges for web notifications and automatically refresh websites,
Replace any dock icon in the window with it (Wow!) by selecting that portion of the window.

Use PiP (Picture-in-Picture) on video sites that support it.
Delete advertising,
Throughout macOS, use floating windows
and many more…
I feel $24.99 one-off for this tool is a great deal, considering all these features. What do you think?
CleanShot X
(Basic: $29 one-off. Pro: $8/month | Available on Setapp)
CleanShot X can achieve things the macOS screenshot tool cannot. Complete screenshot toolkit.
CleanShot X, like Pixel Snap 2 (#3), is fantastic.
Allows
Scroll to capture a long page,
screen recording,
With webcam on,
• With mic and system audio,
• Highlighting mouse clicks and hotkeys.
Maintain floating screenshots for reference
While capturing, conceal desktop icons and notifications.
Recognize text in screenshots (OCR),
You may upload and share screenshots using the built-in cloud.
These are just 6 in 50+ features, and you’re already saying Wow!

Will Lockett
3 years ago
The world will be changed by this molten salt battery.

Four times the energy density and a fraction of lithium-cost ion's
As the globe abandons fossil fuels, batteries become more important. EVs, solar, wind, tidal, wave, and even local energy grids will use them. We need a battery revolution since our present batteries are big, expensive, and detrimental to the environment. A recent publication describes a battery that solves these problems. But will it be enough?
Sodium-sulfur molten salt battery. It has existed for a long time and uses molten salt as an electrolyte (read more about molten salt batteries here). These batteries are cheaper, safer, and more environmentally friendly because they use less eco-damaging materials, are non-toxic, and are non-flammable.
Previous molten salt batteries used aluminium-sulphur chemistries, which had a low energy density and required high temperatures to keep the salt liquid. This one uses a revolutionary sodium-sulphur chemistry and a room-temperature-melting salt, making it more useful, affordable, and eco-friendly. To investigate this, researchers constructed a button-cell prototype and tested it.
First, the battery was 1,017 mAh/g. This battery is four times as energy dense as high-density lithium-ion batteries (250 mAh/g).
No one knows how much this battery would cost. A more expensive molten-salt battery costs $15 per kWh. Current lithium-ion batteries cost $132/kWh. If this new molten salt battery costs the same as present cells, it will be 90% cheaper.
This room-temperature molten salt battery could be utilized in an EV. Cold-weather heaters just need a modest backup battery.
The ultimate EV battery? If used in a Tesla Model S, you could install four times the capacity with no weight gain, offering a 1,620-mile range. This huge battery pack would cost less than Tesla's. This battery would nearly perfect EVs.
Or would it?
The battery's capacity declined by 50% after 1,000 charge cycles. This means that our hypothetical Model S would suffer this decline after 1.6 million miles, but for more cheap vehicles that use smaller packs, this would be too short. This test cell wasn't supposed to last long, so this is shocking. Future versions of this cell could be modified to live longer.
This affordable and eco-friendly cell is best employed as a grid-storage battery for renewable energy. Its safety and affordable price outweigh its short lifespan. Because this battery is made of easily accessible materials, it may be utilized to boost grid-storage capacity without causing supply chain concerns or EV battery prices to skyrocket.
Researchers are designing a bigger pouch cell (like those in phones and laptops) for this purpose. The battery revolution we need could be near. Let’s just hope it isn’t too late.
James Brockbank
3 years ago
Canonical URLs for Beginners
Canonicalization and canonical URLs are essential for SEO, and improper implementation can negatively impact your site's performance.
Canonical tags were introduced in 2009 to help webmasters with duplicate or similar content on multiple URLs.
To use canonical tags properly, you must understand their purpose, operation, and implementation.
Canonical URLs and Tags
Canonical tags tell search engines that a certain URL is a page's master copy. They specify a page's canonical URL. Webmasters can avoid duplicate content by linking to the "canonical" or "preferred" version of a page.
How are canonical tags and URLs different? Can these be specified differently?
Tags
Canonical tags are found in an HTML page's head></head> section.
<link rel="canonical" href="https://www.website.com/page/" />These can be self-referencing or reference another page's URL to consolidate signals.
Canonical tags and URLs are often used interchangeably, which is incorrect.
The rel="canonical" tag is the most common way to set canonical URLs, but it's not the only way.
Canonical URLs
What's a canonical link? Canonical link is the'master' URL for duplicate pages.
In Google's own words:
A canonical URL is the page Google thinks is most representative of duplicate pages on your site.
— Google Search Console Help
You can indicate your preferred canonical URL. For various reasons, Google may choose a different page than you.
When set correctly, the canonical URL is usually your specified URL.
Canonical URLs determine which page will be shown in search results (unless a duplicate is explicitly better for a user, like a mobile version).
Canonical URLs can be on different domains.
Other ways to specify canonical URLs
Canonical tags are the most common way to specify a canonical URL.
You can also set canonicals by:
Setting the HTTP header rel=canonical.
All pages listed in a sitemap are suggested as canonicals, but Google decides which pages are duplicates.
Redirects 301.
Google recommends these methods, but they aren't all appropriate for every situation, as we'll see below. Each has its own recommended uses.
Setting canonical URLs isn't required; if you don't, Google will use other signals to determine the best page version.
To control how your site appears in search engines and to avoid duplicate content issues, you should use canonicalization effectively.
Why Duplicate Content Exists
Before we discuss why you should use canonical URLs and how to specify them in popular CMSs, we must first explain why duplicate content exists. Nobody intentionally duplicates website content.
Content management systems create multiple URLs when you launch a page, have indexable versions of your site, or use dynamic URLs.
Assume the following URLs display the same content to a user:
A search engine sees eight duplicate pages, not one.
URLs #1 and #2: the CMS saves product URLs with and without the category name.
#3, #4, and #5 result from the site being accessible via HTTP, HTTPS, www, and non-www.
#6 is a subdomain mobile-friendly URL.
URL #7 lacks URL #2's trailing slash.
URL #8 uses a capital "A" instead of a lowercase one.
Duplicate content may also exist in URLs like:
https://www.website.com
https://www.website.com/index.php
Duplicate content is easy to create.
Canonical URLs help search engines identify different page variations as a single URL on many sites.
SEO Canonical URLs
Canonical URLs help you manage duplicate content that could affect site performance.
Canonical URLs are a technical SEO focus area for many reasons.
Specify URL for search results
When you set a canonical URL, you tell Google which page version to display.
Which would you click?
https://www.domain.com/page-1/
https://www.domain.com/index.php?id=2
First, probably.
Canonicals tell search engines which URL to rank.
Consolidate link signals on similar pages
When you have duplicate or nearly identical pages on your site, the URLs may get external links.
Canonical URLs consolidate multiple pages' link signals into a single URL.
This helps your site rank because signals from multiple URLs are consolidated into one.
Syndication management
Content is often syndicated to reach new audiences.
Canonical URLs consolidate ranking signals to prevent duplicate pages from ranking and ensure the original content ranks.
Avoid Googlebot duplicate page crawling
Canonical URLs ensure that Googlebot crawls your new pages rather than duplicated versions of the same one across mobile and desktop versions, for example.
Crawl budgets aren't an issue for most sites unless they have 100,000+ pages.
How to Correctly Implement the rel=canonical Tag
Using the header tag rel="canonical" is the most common way to specify canonical URLs.
Adding tags and HTML code may seem daunting if you're not a developer, but most CMS platforms allow canonicals out-of-the-box.
These URLs each have one product.
How to Correctly Implement a rel="canonical" HTTP Header
A rel="canonical" HTTP header can replace canonical tags.
This is how to implement a canonical URL for PDFs or non-HTML documents.
You can specify a canonical URL in your site's.htaccess file using the code below.
<Files "file-to-canonicalize.pdf"> Header add Link "< http://www.website.com/canonical-page/>; rel=\"canonical\"" </Files>301 redirects for canonical URLs
Google says 301 redirects can specify canonical URLs.
Only the canonical URL will exist if you use 301 redirects. This will redirect duplicates.
This is the best way to fix duplicate content across:
HTTPS and HTTP
Non-WWW and WWW
Trailing-Slash and Non-Trailing Slash URLs
On a single page, you should use canonical tags unless you can confidently delete and redirect the page.
Sitemaps' canonical URLs
Google assumes sitemap URLs are canonical, so don't include non-canonical URLs.
This does not guarantee canonical URLs, but is a best practice for sitemaps.
Best-practice Canonical Tag
Once you understand a few simple best practices for canonical tags, spotting and cleaning up duplicate content becomes much easier.
Always include:
One canonical URL per page
If you specify multiple canonical URLs per page, they will likely be ignored.
Correct Domain Protocol
If your site uses HTTPS, use this as the canonical URL. It's easy to reference the wrong protocol, so check for it to catch it early.
Trailing slash or non-trailing slash URLs
Be sure to include trailing slashes in your canonical URL if your site uses them.
Specify URLs other than WWW
Search engines see non-WWW and WWW URLs as duplicate pages, so use the correct one.
Absolute URLs
To ensure proper interpretation, canonical tags should use absolute URLs.
So use:
<link rel="canonical" href="https://www.website.com/page-a/" />And not:
<link rel="canonical" href="/page-a/" />If not canonicalizing, use self-referential canonical URLs.
When a page isn't canonicalizing to another URL, use self-referencing canonical URLs.
Canonical tags refer to themselves here.
Common Canonical Tags Mistakes
Here are some common canonical tag mistakes.
301 Canonicalization
Set the canonical URL as the redirect target, not a redirected URL.
Incorrect Domain Canonicalization
If your site uses HTTPS, don't set canonical URLs to HTTP.
Irrelevant Canonicalization
Canonicalize URLs to duplicate or near-identical content only.
SEOs sometimes try to pass link signals via canonical tags from unrelated content to increase rank. This isn't how canonicalization should be used and should be avoided.
Multiple Canonical URLs
Only use one canonical tag or URL per page; otherwise, they may all be ignored.
When overriding defaults in some CMSs, you may accidentally include two canonical tags in your page's <head>.
Pagination vs. Canonicalization
Incorrect pagination can cause duplicate content. Canonicalizing URLs to the first page isn't always the best solution.
Canonicalize to a 'view all' page.
How to Audit Canonical Tags (and Fix Issues)
Audit your site's canonical tags to find canonicalization issues.
SEMrush Site Audit can help. You'll find canonical tag checks in your website's site audit report.
Let's examine these issues and their solutions.
No Canonical Tag on AMP
Site Audit will flag AMP pages without canonical tags.
Canonicalization between AMP and non-AMP pages is important.
Add a rel="canonical" tag to each AMP page's head>.
No HTTPS redirect or canonical from HTTP homepage
Duplicate content issues will be flagged in the Site Audit if your site is accessible via HTTPS and HTTP.
You can fix this by 301 redirecting or adding a canonical tag to HTTP pages that references HTTPS.
Broken canonical links
Broken canonical links won't be considered canonical URLs.
This error could mean your canonical links point to non-existent pages, complicating crawling and indexing.
Update broken canonical links to the correct URLs.
Multiple canonical URLs
This error occurs when a page has multiple canonical URLs.
Remove duplicate tags and leave one.
Canonicalization is a key SEO concept, and using it incorrectly can hurt your site's performance.
Once you understand how it works, what it does, and how to find and fix issues, you can use it effectively to remove duplicate content from your site.
Canonicalization SEO Myths
You might also like

Emma Jade
3 years ago
6 hacks to create content faster
Content gurus' top time-saving hacks.

I'm a content strategist, writer, and graphic designer. Time is more valuable than money.
Money is always available. Even if you're poor. Ways exist.
Time is passing, and one day we'll run out.
Sorry to be morbid.
In today's digital age, you need to optimize how you create content for your organization. Here are six content creation hacks.
1. Use templates
Use templates to streamline your work whether generating video, images, or documents.
Setup can take hours. Using a free resource like Canva, you can create templates for any type of material.
This will save you hours each month.
2. Make a content calendar
You post without a plan? A content calendar solves 50% of these problems.
You can prepare, organize, and plan your material ahead of time so you're not scrambling when you remember, "Shit, it's Mother's Day!"
3. Content Batching
Batching content means creating a lot in one session. This is helpful for video content that requires a lot of setup time.
Batching monthly content saves hours. Time is a valuable resource.
When working on one type of task, it's easy to get into a flow state. This saves time.
4. Write Caption
On social media, we generally choose the image first and then the caption. Writing captions first sometimes work better, though.
Writing the captions first can allow you more creative flexibility and be easier if you're not excellent with language.
Say you want to tell your followers something interesting.
Writing a caption first is easier than choosing an image and then writing a caption to match.
Not everything works. You may have already-created content that needs captioning. When you don't know what to share, think of a concept, write the description, and then produce a video or graphic.
Cats can be skinned in several ways..
5. Repurpose
Reuse content when possible. You don't always require new stuff. In fact, you’re pretty stupid if you do #SorryNotSorry.
Repurpose old content. All those blog entries, videos, and unfinished content on your desk or hard drive.
This blog post can be turned into a social media infographic. Canva's motion graphic function can animate it. I can record a YouTube video regarding this issue for a podcast. I can make a post on each point in this blog post and turn it into an eBook or paid course.
And it doesn’t stop there.
My point is, to think outside the box and really dig deep into ways you can leverage the content you’ve already created.
6. Schedule Them
If you're still manually posting content, get help. When you batch your content, schedule it ahead of time.
Some scheduling apps are free or cheap. No excuses.
Don't publish and ghost.
Scheduling saves time by preventing you from doing it manually. But if you never engage with your audience, the algorithm won't reward your material.
Be online and engage your audience.
Content Machine
Use these six content creation hacks. They help you succeed and save time.

Sara_Mednick
3 years ago
Since I'm a scientist, I oppose biohacking
Understanding your own energy depletion and restoration is how to truly optimize

Hack has meant many bad things for centuries. In the 1800s, a hack was a meager horse used to transport goods.
Modern usage describes a butcher or ax murderer's cleaver chop. The 1980s programming boom distinguished elegant code from "hacks". Both got you to your goal, but the latter made any programmer cringe and mutter about changing the code. From this emerged the hacker trope, the friendless anti-villain living in a murky hovel lit by the computer monitor, eating junk food and breaking into databases to highlight security system failures or steal hotdog money.

Now, start-a-billion-dollar-business-from-your-garage types have shifted their sights from app development to DIY biology, coining the term "bio-hack". This is a required keyword and meta tag for every fitness-related podcast, book, conference, app, or device.
Bio-hacking involves bypassing your body and mind's security systems to achieve a goal. Many biohackers' initial goals were reasonable, like lowering blood pressure and weight. Encouraged by their own progress, self-determination, and seemingly exquisite control of their biology, they aimed to outsmart aging and death to live 180 to 1000 years (summarized well in this vox.com article).
With this grandiose north star, the hunt for novel supplements and genetic engineering began.
Companies selling do-it-yourself biological manipulations cite lab studies in mice as proof of their safety and success in reversing age-related diseases or promoting longevity in humans (the goal changes depending on whether a company is talking to the federal government or private donors).
The FDA is slower than science, they say. Why not alter your biochemistry by buying pills online, editing your DNA with a CRISPR kit, or using a sauna delivered to your home? How about a microchip or electrical stimulator?
What could go wrong?
I'm not the neo-police, making citizen's arrests every time someone introduces a new plumbing gadget or extrapolates from animal research on resveratrol or catechins that we should drink more red wine or eat more chocolate. As a scientist who's spent her career asking, "Can we get better?" I've come to view bio-hacking as misguided, profit-driven, and counterproductive to its followers' goals.
We're creatures of nature. Despite all the new gadgets and bio-hacks, we still use Roman plumbing technology, and the best way to stay fit, sharp, and happy is to follow a recipe passed down since the beginning of time. Bacteria, plants, and all natural beings are rhythmic, with alternating periods of high activity and dormancy, whether measured in seconds, hours, days, or seasons. Nature repeats successful patterns.
During the Upstate, every cell in your body is naturally primed and pumped full of glycogen and ATP (your cells' energy currencies), as well as cortisol, which supports your muscles, heart, metabolism, cognitive prowess, emotional regulation, and general "get 'er done" attitude. This big energy release depletes your batteries and requires the Downstate, when your subsystems recharge at the cellular level.
Downstates are when you give your heart a break from pumping nutrient-rich blood through your body; when you give your metabolism a break from inflammation, oxidative stress, and sympathetic arousal caused by eating fast food — or just eating too fast; or when you give your mind a chance to wander, think bigger thoughts, and come up with new creative solutions. When you're responding to notifications, emails, and fires, you can't relax.
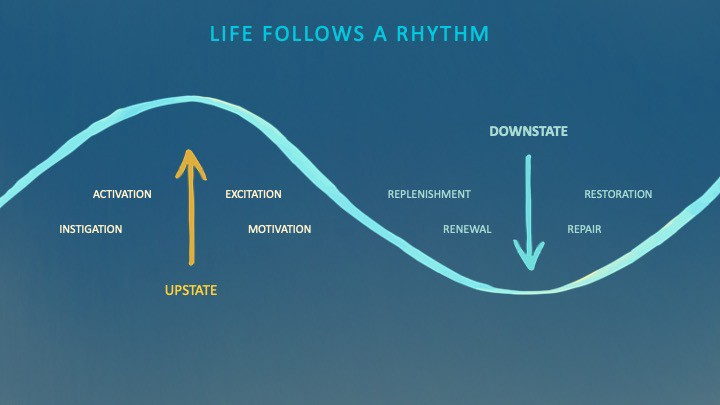
Downstates aren't just for consistently recharging your battery. By spending time in the Downstate, your body and brain get extra energy and nutrients, allowing you to grow smarter, faster, stronger, and more self-regulated. This state supports half-marathon training, exam prep, and mediation. As we age, spending more time in the Downstate is key to mental and physical health, well-being, and longevity.
When you prioritize energy-demanding activities during Upstate periods and energy-replenishing activities during Downstate periods, all your subsystems, including cardiovascular, metabolic, muscular, cognitive, and emotional, hum along at their optimal settings. When you synchronize the Upstates and Downstates of these individual rhythms, their functioning improves. A hard workout causes autonomic stress, which triggers Downstate recovery.
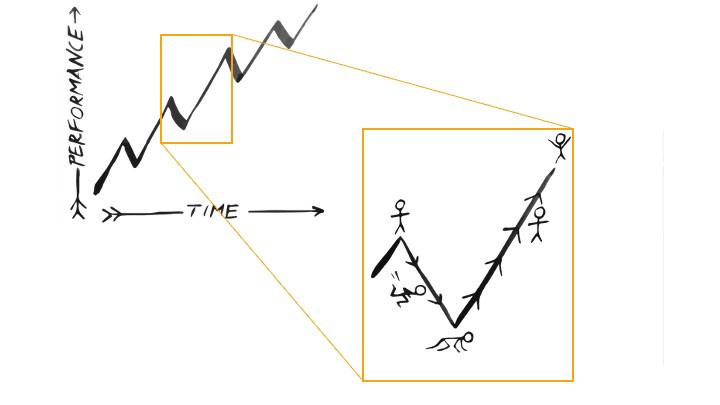
By choosing the right timing and type of exercise during the day, you can ensure a deeper recovery and greater readiness for the next workout by working with your natural rhythms and strengthening your autonomic and sleep Downstates.
Morning cardio workouts increase deep sleep compared to afternoon workouts. Timing and type of meals determine when your sleep hormone melatonin is released, ushering in sleep.
Rhythm isn't a hack. It's not a way to cheat the system or the boss. Nature has honed its optimization wisdom over trillions of days and nights. Stop looking for quick fixes. You're a whole system made of smaller subsystems that must work together to function well. No one pill or subsystem will make it all work. Understanding and coordinating your rhythms is free, easy, and only benefits you.
Dr. Sara C. Mednick is a cognitive neuroscientist at UC Irvine and author of The Power of the Downstate (HachetteGO)

Jano le Roux
3 years ago
My Top 11 Tools For Building A Modern Startup, With A Free Plan
The best free tools are probably unknown to you.
Modern startups are easy to build.
Start with free tools.
Let’s go.
Web development — Webflow
Code-free HTML, CSS, and JS.
Webflow isn't like Squarespace, Wix, or Shopify.
It's a super-fast no-code tool for professionals to construct complex, highly-responsive websites and landing pages.
Webflow can help you add animations like those on Apple's website to your own site.
I made the jump from WordPress a few years ago and it changed my life.
No damn plugins. No damn errors. No damn updates.
The best, you can get started on Webflow for free.
Data tracking — Airtable
Spreadsheet wings.
Airtable combines spreadsheet flexibility with database power without code.
Airtable is modern.
Airtable has modularity.
Scaling Airtable is simple.
Airtable, one of the most adaptable solutions on this list, is perfect for client data management.
Clients choose customized service packages. Airtable consolidates data so you can automate procedures like invoice management and focus on your strengths.
Airtable connects with so many tools that rarely creates headaches. Airtable scales when you do.
Airtable's flexibility makes it a potential backend database.
Design — Figma
Better, faster, easier user interface design.
Figma rocks!
It’s fast.
It's free.
It's adaptable
First, design in Figma.
Iterate.
Export development assets.
Figma lets you add more team members as your company grows to work on each iteration simultaneously.
Figma is web-based, so you don't need a powerful PC or Mac to start.
Task management — Trello
Unclock jobs.
Tacky and terrifying task management products abound. Trello isn’t.
Those that follow Marie Kondo will appreciate Trello.
Everything is clean.
Nothing is complicated.
Everything has a place.
Compared to other task management solutions, Trello is limited. And that’s good. Too many buttons lead to too many decisions lead to too many hours wasted.
Trello is a must for teamwork.
Domain email — Zoho
Free domain email hosting.
Professional email is essential for startups. People relied on monthly payments for too long. Nope.
Zoho offers 5 free professional emails.
It doesn't have Google's UI, but it works.
VPN — Proton VPN
Fast Swiss VPN protects your data and privacy.
Proton VPN is secure.
Proton doesn't record any data.
Proton is based in Switzerland.
Swiss privacy regulation is among the most strict in the world, therefore user data are protected. Switzerland isn't a 14 eye country.
Journalists and activists trust Proton to secure their identities while accessing and sharing information authoritarian governments don't want them to access.
Web host — Netlify
Free fast web hosting.
Netlify is a scalable platform that combines your favorite tools and APIs to develop high-performance sites, stores, and apps through GitHub.
Serverless functions and environment variables preserve API keys.
Netlify's free tier is unmissable.
100GB of free monthly bandwidth.
Free 125k serverless operations per website each month.
Database — MongoDB
Create a fast, scalable database.
MongoDB is for small and large databases. It's a fast and inexpensive database.
Free for the first million reads.
Then, for each million reads, you must pay $0.10.
MongoDB's free plan has:
Encryption from end to end
Continual authentication
field-level client-side encryption
If you have a large database, you can easily connect MongoDB to Webflow to bypass CMS limits.
Automation — Zapier
Time-saving tip: automate repetitive chores.
Zapier simplifies life.
Zapier syncs and connects your favorite apps to do impossibly awesome things.
If your online store is connected to Zapier, a customer's purchase can trigger a number of automated actions, such as:
The customer is being added to an email chain.
Put the information in your Airtable.
Send a pre-programmed postcard to the customer.
Alexa, set the color of your smart lights to purple.
Zapier scales when you do.
Email & SMS marketing — Omnisend
Email and SMS marketing campaigns.
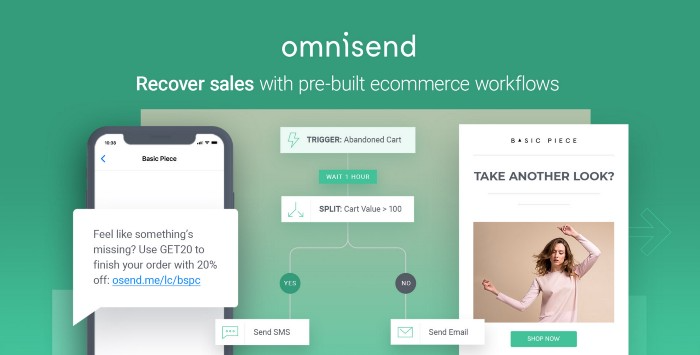
This is an excellent Mailchimp option for magical emails. Omnisend's processes simplify email automation.
I love the interface's cleanliness.
Omnisend's free tier includes web push notifications.
Send up to:
500 emails per month
60 maximum SMSs
500 Web Push Maximum
Forms and surveys — Tally
Create flexible forms that people enjoy.
Typeform is clean but restricting. Sometimes you need to add many questions. Tally's needed sometimes.
Tally is flexible and cheaper than Typeform.
99% of Tally's features are free and unrestricted, including:
Unlimited forms
Countless submissions
Collect payments
File upload
Tally lets you examine what individuals contributed to forms before submitting them to see where they get stuck.
Airtable and Zapier connectors automate things further. If you pay, you can apply custom CSS to fit your brand.
See.
Free tools are the greatest.
Let's use them to launch a startup.