More on Web3 & Crypto
Langston Thomas
3 years ago
A Simple Guide to NFT Blockchains
Ethereum's blockchain rules NFTs. Many consider it the one-stop shop for NFTs, and it's become the most talked-about and trafficked blockchain in existence.
Other blockchains are becoming popular in NFTs. Crypto-artists and NFT enthusiasts have sought new places to mint and trade NFTs due to Ethereum's high transaction costs and environmental impact.
When choosing a blockchain to mint on, there are several factors to consider. Size, creator costs, consumer spending habits, security, and community input are important. We've created a high-level summary of blockchains for NFTs to help clarify the fast-paced world of web3 tech.
Ethereum
Ethereum currently has the most NFTs. It's decentralized and provides financial and legal services without intermediaries. It houses popular NFT marketplaces (OpenSea), projects (CryptoPunks and the Bored Ape Yacht Club), and artists (Pak and Beeple).
It's also expensive and energy-intensive. This is because Ethereum works using a Proof-of-Work (PoW) mechanism. PoW requires computers to solve puzzles to add blocks and transactions to the blockchain. Solving these puzzles requires a lot of computer power, resulting in astronomical energy loss.
You should consider this blockchain first due to its popularity, security, decentralization, and ease of use.
Solana
Solana is a fast programmable blockchain. Its proof-of-history and proof-of-stake (PoS) consensus mechanisms eliminate complex puzzles. Reduced validation times and fees result.
PoS users stake their cryptocurrency to become a block validator. Validators get SOL. This encourages and rewards users to become stakers. PoH works with PoS to cryptographically verify time between events. Solana blockchain ensures transactions are in order and found by the correct leader (validator).
Solana's PoS and PoH mechanisms keep transaction fees and times low. Solana isn't as popular as Ethereum, so there are fewer NFT marketplaces and blockchain traders.
Tezos
Tezos is a greener blockchain. Tezos rose in 2021. Hic et Nunc was hailed as an economic alternative to Ethereum-centric marketplaces until Nov. 14, 2021.
Similar to Solana, Tezos uses a PoS consensus mechanism and only a PoS mechanism to reduce computational work. This blockchain uses two million times less energy than Ethereum. It's cheaper than Ethereum (but does cost more than Solana).
Tezos is a good place to start minting NFTs in bulk. Objkt is the largest Tezos marketplace.
Flow
Flow is a high-performance blockchain for NFTs, games, and decentralized apps (dApps). Flow is built with scalability in mind, so billions of people could interact with NFTs on the blockchain.
Flow became the NBA's blockchain partner in 2019. Flow, a product of Dapper labs (the team behind CryptoKitties), launched and hosts NBA Top Shot, making the blockchain integral to the popularity of non-fungible tokens.
Flow uses PoS to verify transactions, like Tezos. Developers are working on a model to handle 10,000 transactions per second on the blockchain. Low transaction fees.
Flow NFTs are tradeable on Blocktobay, OpenSea, Rarible, Foundation, and other platforms. NBA, NFL, UFC, and others have launched NFT marketplaces on Flow. Flow isn't as popular as Ethereum, resulting in fewer NFT marketplaces and blockchain traders.
Asset Exchange (WAX)
WAX is king of virtual collectibles. WAX is popular for digitalized versions of legacy collectibles like trading cards, figurines, memorabilia, etc.
Wax uses a PoS mechanism, but also creates carbon offset NFTs and partners with Climate Care. Like Flow, WAX transaction fees are low, and network fees are redistributed to the WAX community as an incentive to collectors.
WAX marketplaces host Topps, NASCAR, Hot Wheels, and cult classic film franchises like Godzilla, The Princess Bride, and Spiderman.
Binance Smart Chain
BSC is another good option for balancing fees and performance. High-speed transactions and low fees hurt decentralization. BSC is most centralized.
Binance Smart Chain uses Proof of Staked Authority (PoSA) to support a short block time and low fees. The 21 validators needed to run the exchange switch every 24 hours. 11 of the 21 validators are directly connected to the Binance Crypto Exchange, according to reports.
While many in the crypto and NFT ecosystems dislike centralization, the BSC NFT market picked up speed in 2021. OpenBiSea, AirNFTs, JuggerWorld, and others are gaining popularity despite not having as robust an ecosystem as Ethereum.

Shan Vernekar
3 years ago
How the Ethereum blockchain's transactions are carried out
Overview
Ethereum blockchain is a network of nodes that validate transactions. Any network node can be queried for blockchain data for free. To write data as a transition requires processing and writing to each network node's storage. Fee is paid in ether and is also called as gas.
We'll examine how user-initiated transactions flow across the network and into the blockchain.
Flow of transactions
A user wishes to move some ether from one external account to another. He utilizes a cryptocurrency wallet for this (like Metamask), which is a browser extension.
The user enters the desired transfer amount and the external account's address. He has the option to choose the transaction cost he is ready to pay.
Wallet makes use of this data, signs it with the user's private key, and writes it to an Ethereum node. Services such as Infura offer APIs that enable writing data to nodes. One of these services is used by Metamask. An example transaction is shown below. Notice the “to” address and value fields.
var rawTxn = {
nonce: web3.toHex(txnCount),
gasPrice: web3.toHex(100000000000),
gasLimit: web3.toHex(140000),
to: '0x633296baebc20f33ac2e1c1b105d7cd1f6a0718b',
value: web3.toHex(0),
data: '0xcc9ab24952616d6100000000000000000000000000000000000000000000000000000000'
};The transaction is written to the target Ethereum node's local TRANSACTION POOL. It informed surrounding nodes of the new transaction, and those nodes reciprocated. Eventually, this transaction is received by and written to each node's local TRANSACTION pool.
The miner who finds the following block first adds pending transactions (with a higher gas cost) from the nearby TRANSACTION POOL to the block.
The transactions written to the new block are verified by other network nodes.
A block is added to the main blockchain after there is consensus and it is determined to be genuine. The local blockchain is updated with the new node by additional nodes as well.
Block mining begins again next.
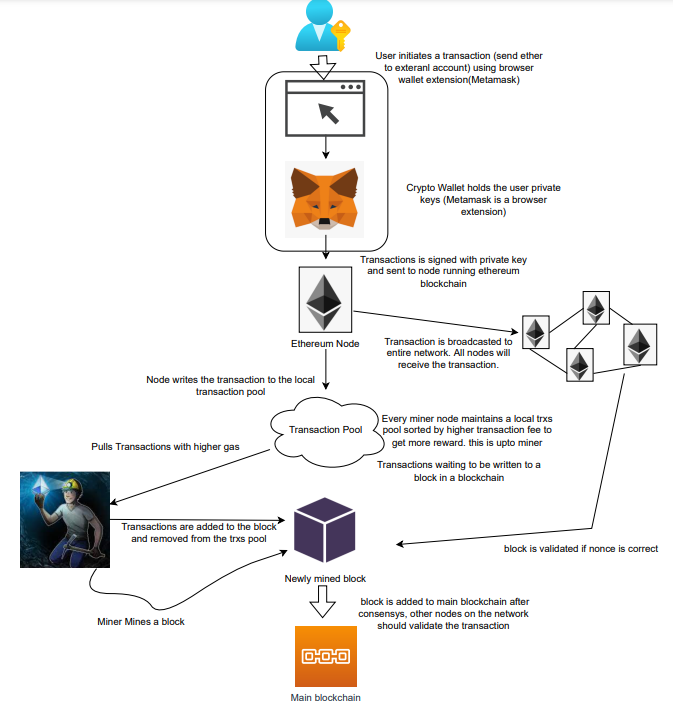
The image above shows how transactions go via the network and what's needed to submit them to the main block chain.
References
ethereum.org/transactions How Ethereum transactions function, their data structure, and how to send them via app. ethereum.org

Stephen Moore
3 years ago
Web 2 + Web 3 = Web 5.
Monkey jpegs and shitcoins have tarnished Web3's reputation. Let’s move on.

Web3 was called "the internet's future."
Well, 'crypto bros' shouted about it loudly.
As quickly as it arrived to be the next internet, it appears to be dead. It's had scandals, turbulence, and crashes galore:
Web 3.0's cryptocurrencies have crashed. Bitcoin's all-time high was $66,935. This month, Ethereum fell from $2130 to $1117. Six months ago, the cryptocurrency market peaked at $3 trillion. Worst is likely ahead.
Gas fees make even the simplest Web3 blockchain transactions unsustainable.
Terra, Luna, and other dollar pegs collapsed, hurting crypto markets. Celsius, a crypto lender backed by VCs and Canada's second-largest pension fund, and Binance, a crypto marketplace, have withheld money and coins. They're near collapse.
NFT sales are falling rapidly and losing public interest.
Web3 has few real-world uses, like most crypto/blockchain technologies. Web3's image has been tarnished by monkey profile pictures and shitcoins while failing to become decentralized (the whole concept is controlled by VCs).
The damage seems irreparable, leaving Web3 in the gutter.
Step forward our new saviour — Web5
Fear not though, as hero awaits to drag us out of the Web3 hellscape. Jack Dorsey revealed his plan to save the internet quickly.
Dorsey has long criticized Web3, believing that VC capital and silicon valley insiders have created a centralized platform. In a tweet that upset believers and VCs (he was promptly blocked by Marc Andreessen), Dorsey argued, "You don't own "Web3." VCs and LPs do. Their incentives prevent it. It's a centralized organization with a new name.
Dorsey announced Web5 on June 10 in a very Elon-like manner. Block's TBD unit will work on the project (formerly Square).
Web5's pitch is that users will control their own data and identity. Bitcoin-based. Sound familiar? The presentation pack's official definition emphasizes decentralization. Web5 is a decentralized web platform that enables developers to write decentralized web apps using decentralized identifiers, verifiable credentials, and decentralized web nodes, returning ownership and control over identity and data to individuals.
Web5 would be permission-less, open, and token-less. What that means for Earth is anyone's guess. Identity. Ownership. Blockchains. Bitcoin. Different.
Web4 appears to have been skipped, forever destined to wish it could have shown the world what it could have been. (It was probably crap.) As this iteration combines Web2 and Web3, simple math and common sense add up to 5. Or something.
Dorsey and his team have had this idea simmering for a while. Daniel Buchner, a member of Block's Decentralized Identity team, said, "We're finishing up Web5's technical components."
Web5 could be the project that decentralizes the internet. It must be useful to users and convince everyone to drop the countless Web3 projects, products, services, coins, blockchains, and websites being developed as I write this.
Web5 may be too late for Dorsey and the incoming flood of creators.
Web6 is planned!
The next months and years will be hectic and less stable than the transition from Web 1.0 to Web 2.0.
Web1 was around 1991-2004.
Web2 ran from 2004 to 2021. (though the Web3 term was first used in 2014, it only really gained traction years later.)
Web3 lasted a year.
Web4 is dead.
Silicon Valley billionaires are turning it into a startup-style race, each disrupting the next iteration until they crack it. Or destroy it completely.
Web5 won't last either.
You might also like

Emma Jade
3 years ago
6 hacks to create content faster
Content gurus' top time-saving hacks.

I'm a content strategist, writer, and graphic designer. Time is more valuable than money.
Money is always available. Even if you're poor. Ways exist.
Time is passing, and one day we'll run out.
Sorry to be morbid.
In today's digital age, you need to optimize how you create content for your organization. Here are six content creation hacks.
1. Use templates
Use templates to streamline your work whether generating video, images, or documents.
Setup can take hours. Using a free resource like Canva, you can create templates for any type of material.
This will save you hours each month.
2. Make a content calendar
You post without a plan? A content calendar solves 50% of these problems.
You can prepare, organize, and plan your material ahead of time so you're not scrambling when you remember, "Shit, it's Mother's Day!"
3. Content Batching
Batching content means creating a lot in one session. This is helpful for video content that requires a lot of setup time.
Batching monthly content saves hours. Time is a valuable resource.
When working on one type of task, it's easy to get into a flow state. This saves time.
4. Write Caption
On social media, we generally choose the image first and then the caption. Writing captions first sometimes work better, though.
Writing the captions first can allow you more creative flexibility and be easier if you're not excellent with language.
Say you want to tell your followers something interesting.
Writing a caption first is easier than choosing an image and then writing a caption to match.
Not everything works. You may have already-created content that needs captioning. When you don't know what to share, think of a concept, write the description, and then produce a video or graphic.
Cats can be skinned in several ways..
5. Repurpose
Reuse content when possible. You don't always require new stuff. In fact, you’re pretty stupid if you do #SorryNotSorry.
Repurpose old content. All those blog entries, videos, and unfinished content on your desk or hard drive.
This blog post can be turned into a social media infographic. Canva's motion graphic function can animate it. I can record a YouTube video regarding this issue for a podcast. I can make a post on each point in this blog post and turn it into an eBook or paid course.
And it doesn’t stop there.
My point is, to think outside the box and really dig deep into ways you can leverage the content you’ve already created.
6. Schedule Them
If you're still manually posting content, get help. When you batch your content, schedule it ahead of time.
Some scheduling apps are free or cheap. No excuses.
Don't publish and ghost.
Scheduling saves time by preventing you from doing it manually. But if you never engage with your audience, the algorithm won't reward your material.
Be online and engage your audience.
Content Machine
Use these six content creation hacks. They help you succeed and save time.

Claire Berehova
3 years ago
There’s no manual for that
| Kyiv oblast in springtime. Photo by author. |
We’ve been receiving since the war began text messages from the State Emergency Service of Ukraine every few days. They’ve contained information on how to comfort a child and what to do in case of a water outage.
But a question that I struggle to suppress irks within me: How would we know if there really was a threat coming our away? So how can I happily disregard an air raid siren and continue singing to my three-month-old son when I feel like a World War II film became reality? There’s no manual for that.
Along with the anxiety, there’s the guilt that always seems to appear alongside dinner we’re fortunate to still have each evening while brave Ukrainian soldiers are facing serious food insecurity. There’s no manual for how to deal with this guilt.
When it comes to the enemy, there is no manual for how to react to the news of Russian casualties. Every dead Russian soldier weakens Putin, but I also know that many of these men had wives and girlfriends who are now living a nightmare.
So, I felt like I had to start writing my own manual.
The anxiety around the air raid siren? Only with time does it get easier to ignore it, but never completely.
The guilt? All we can do is pray.
That inner conflict? As Russia continues to stun the world with its war crimes, my emotions get less gray — I have to get used to accommodating absurd levels of hatred.
Sadness? It feels a bit more manageable when we laugh, and a little alcohol helps (as it usually does).
Cabin fever? Step outside in the yard when possible. At least the sunshine is becoming more fervent with spring approaching.
Slava Ukraini. Heroyam slava. (Glory to Ukraine. Glory to the heroes.)
Nate Kostar
3 years ago
# DeaMau5’s PIXELYNX and Beatport Launch Festival NFTs
Pixelynx, a music metaverse gaming platform, has teamed up with Beatport, an online music retailer focusing in electronic music, to establish a Synth Heads non-fungible token (NFT) Collection.
Richie Hawtin, aka Deadmau5, and Joel Zimmerman, nicknamed Pixelynx, have invented a new music metaverse game platform called Pixelynx. In January 2022, they released their first Beatport NFT drop, which saw 3,030 generative NFTs sell out in seconds.
The limited edition Synth Heads NFTs will be released in collaboration with Junction 2, the largest UK techno festival, and having one will grant fans special access tickets and experiences at the London-based festival.
Membership in the Synth Head community, day passes to the Junction 2 Festival 2022, Junction 2 and Beatport apparel, special vinyl releases, and continued access to future ticket drops are just a few of the experiences available.
Five lucky NFT holders will also receive a Golden Ticket, which includes access to a backstage artist bar and tickets to Junction 2's next large-scale London event this summer, in addition to full festival entrance for both days.
The Junction 2 festival will take place at Trent Park in London on June 18th and 19th, and will feature performances from Four Tet, Dixon, Amelie Lens, Robert Hood, and a slew of other artists. Holders of the original Synth Head NFT will be granted admission to the festival's guestlist as well as line-jumping privileges.
The new Synth Heads NFTs collection contain 300 NFTs.
NFTs that provide IRL utility are in high demand.
The benefits of NFT drops related to In Real Life (IRL) utility aren't limited to Beatport and Pixelynx.
Coachella, a well-known music event, recently partnered with cryptocurrency exchange FTX to offer free NFTs to 2022 pass holders. Access to a dedicated entry lane, a meal and beverage pass, and limited-edition merchandise were all included with the NFTs.
Coachella also has its own NFT store on the Solana blockchain, where fans can buy Coachella NFTs and digital treasures that unlock exclusive on-site experiences, physical objects, lifetime festival passes, and "future adventures."
Individual artists and performers have begun taking advantage of NFT technology outside of large music festivals like Coachella.
DJ Tisto has revealed that he would release a VIP NFT for his upcoming "Eagle" collection during the EDC festival in Las Vegas in 2022. This NFT, dubbed "All Access Eagle," gives collectors the best chance to get NFTs from his first drop, as well as unique access to the music "Repeat It."
NFTs are one-of-a-kind digital assets that can be verified, purchased, sold, and traded on blockchains, opening up new possibilities for artists and businesses alike. Time will tell whether Beatport and Pixelynx's Synth Head NFT collection will be successful, but if it's anything like the first release, it's a safe bet.
