More on Web3 & Crypto
Olga Kharif
3 years ago
A month after freezing customer withdrawals, Celsius files for bankruptcy.

Alex Mashinsky, CEO of Celsius, speaks at Web Summit 2021 in Lisbon.
Celsius Network filed for Chapter 11 bankruptcy a month after freezing customer withdrawals, joining other crypto casualties.
Celsius took the step to stabilize its business and restructure for all stakeholders. The filing was done in the Southern District of New York.
The company, which amassed more than $20 billion by offering 18% interest on cryptocurrency deposits, paused withdrawals and other functions in mid-June, citing "extreme market conditions."
As the Fed raises interest rates aggressively, it hurts risk sentiment and squeezes funding costs. Voyager Digital Ltd. filed for Chapter 11 bankruptcy this month, and Three Arrows Capital has called in liquidators.
Celsius called the pause "difficult but necessary." Without the halt, "the acceleration of withdrawals would have allowed certain customers to be paid in full while leaving others to wait for Celsius to harvest value from illiquid or longer-term asset deployment activities," it said.
Celsius declined to comment. CEO Alex Mashinsky said the move will strengthen the company's future.
The company wants to keep operating. It's not requesting permission to allow customer withdrawals right now; Chapter 11 will handle customer claims. The filing estimates assets and liabilities between $1 billion and $10 billion.
Celsius is advised by Kirkland & Ellis, Centerview Partners, and Alvarez & Marsal.
Yield-promises
Celsius promised 18% returns on crypto loans. It lent those coins to institutional investors and participated in decentralized-finance apps.
When TerraUSD (UST) and Luna collapsed in May, Celsius pulled its funds from Terra's Anchor Protocol, which offered 20% returns on UST deposits. Recently, another large holding, staked ETH, or stETH, which is tied to Ether, became illiquid and discounted to Ether.
The lender is one of many crypto companies hurt by risky bets in the bear market. Also, Babel halted withdrawals. Voyager Digital filed for bankruptcy, and crypto hedge fund Three Arrows Capital filed for Chapter 15 bankruptcy.
According to blockchain data and tracker Zapper, Celsius repaid all of its debt in Aave, Compound, and MakerDAO last month.
Celsius charged Symbolic Capital Partners Ltd. 2,000 Ether as collateral for a cash loan on June 13. According to company filings, Symbolic was charged 2,545.25 Ether on June 11.
In July 6 filings, it said it reshuffled its board, appointing two new members and firing others.

Matt Ward
3 years ago
Is Web3 nonsense?
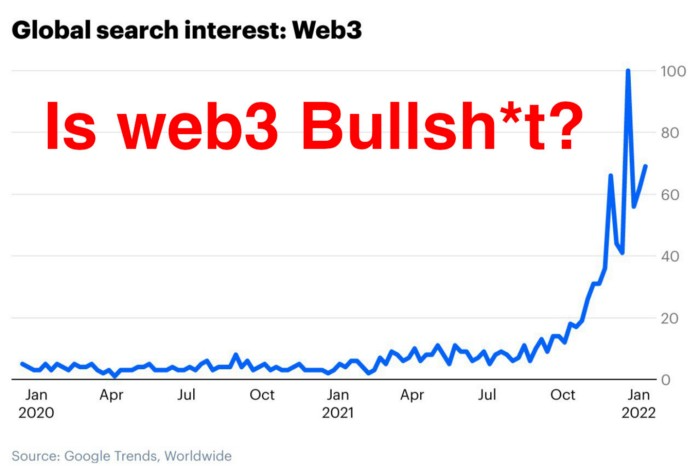
Crypto and blockchain have rebranded as web3. They probably thought it sounded better and didn't want the baggage of scam ICOs, STOs, and skirted securities laws.
It was like Facebook becoming Meta. Crypto's biggest players wanted to change public (and regulator) perception away from pump-and-dump schemes.
After the 2018 ICO gold rush, it's understandable. Every project that raised millions (or billions) never shipped a meaningful product.
Like many crazes, charlatans took the money and ran.
Despite its grifter past, web3 is THE hot topic today as more founders, venture firms, and larger institutions look to build the future decentralized internet.
Supposedly.
How often have you heard: This will change the world, fix the internet, and give people power?
Why are most of web3's biggest proponents (and beneficiaries) the same rich, powerful players who built and invested in the modern internet? It's like they want to remake and own the internet.
Something seems off about that.
Why are insiders getting preferential presale terms before the public, allowing early investors and proponents to flip dirt cheap tokens and advisors shares almost immediately after the public sale?
It's a good gig with guaranteed markups, no risk or progress.
If it sounds like insider trading, it is, at least practically. This is clear when people talk about blockchain/web3 launches and tokens.
Fast money, quick flips, and guaranteed markups/returns are common.
Incentives-wise, it's hard to blame them. Who can blame someone for following the rules to win? Is it their fault or regulators' for not leveling the playing field?
It's similar to oil companies polluting for profit, Instagram depressing you into buying a new dress, or pharma pushing an unnecessary pill.
All of that is fair game, at least until we change the playbook, because people (and corporations) change for pain or love. Who doesn't love money?
belief based on money gain
Sinclair:
“It is difficult to get a man to understand something when his salary depends upon his not understanding it.”
Bitcoin, blockchain, and web3 analogies?
Most blockchain and web3 proponents are true believers, not cynical capitalists. They believe blockchain's inherent transparency and permissionless trust allow humanity to evolve beyond our reptilian ways and build a better decentralized and democratic world.
They highlight issues with the modern internet and monopoly players like Google, Facebook, and Apple. Decentralization fixes everything
If we could give power back to the people and get governments/corporations/individuals out of the way, we'd fix everything.
Blockchain solves supply chain and child labor issues in China.
To meet Paris climate goals, reduce emissions. Create a carbon token.
Fixing online hatred and polarization Web3 Twitter and Facebook replacement.

Web3 must just be the answer for everything… your “perfect” silver bullet.
Nothing fits everyone. Blockchain has pros and cons like everything else.
Blockchain's viral, ponzi-like nature has an MLM (mid level marketing) feel. If you bought Taylor Swift's NFT, your investment is tied to her popularity.
Probably makes you promote Swift more. Play music loudly.
Here's another example:
Imagine if Jehovah’s Witnesses (or evangelical preachers…) got paid for every single person they converted to their cause.
It becomes a self-fulfilling prophecy as their faith and wealth grow.
Which breeds extremism? Ultra-Orthodox Jews are an example. maximalists

Bitcoin and blockchain are causes, religions. It's a money-making movement and ideal.
We're good at convincing ourselves of things we want to believe, hence filter bubbles.
I ignore anything that doesn't fit my worldview and seek out like-minded people, which algorithms amplify.
Then what?
Is web3 merely a new scam?
No, never!
Blockchain has many crucial uses.
Sending money home/abroad without bank fees;
Like fleeing a war-torn country and converting savings to Bitcoin;
Like preventing Twitter from silencing dissidents.
Permissionless, trustless databases could benefit society and humanity. There are, however, many limitations.
Lost password?
What if you're cheated?
What if Trump/Putin/your favorite dictator incites a coup d'état?
What-ifs abound. Decentralization's openness brings good and bad.
No gatekeepers or firefighters to rescue you.
ISIS's fundraising is also frictionless.
Community-owned apps with bad interfaces and service.
Trade-offs rule.
So what compromises does web3 make?
What are your trade-offs? Decentralization has many strengths and flaws. Like Bitcoin's wasteful proof-of-work or Ethereum's political/wealth-based proof-of-stake.
To ensure the survival and veracity of the network/blockchain and to safeguard its nodes, extreme measures have been designed/put in place to prevent hostile takeovers aimed at altering the blockchain, i.e., adding money to your own wallet (account), etc.
These protective measures require significant resources and pose challenges. Reduced speed and throughput, high gas fees (cost to submit/write a transaction to the blockchain), and delayed development times, not to mention forked blockchain chains oops, web3 projects.
Protecting dissidents or rogue regimes makes sense. You need safety, privacy, and calm.
First-world life?
What if you assumed EVERYONE you saw was out to rob/attack you? You'd never travel, trust anyone, accomplish much, or live fully. The economy would collapse.
It's like an ant colony where half the ants do nothing but wait to be attacked.
Waste of time and money.
11% of the US budget goes to the military. Imagine what we could do with the $766B+ we spend on what-ifs annually.
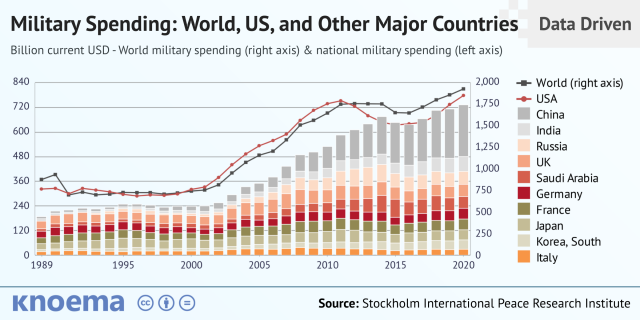
Is so much hypothetical security needed?
Blockchain and web3 are similar.
Does your app need permissionless decentralization? Does your scooter-sharing company really need a proof-of-stake system and 1000s of nodes to avoid Russian hackers? Why?
Worst-case scenario? It's not life or death, unless you overstate the what-ifs. Web3 proponents find improbable scenarios to justify decentralization and tokenization.
Do I need a token to prove ownership of my painting? Unless I'm a master thief, I probably bought it.
despite losing the receipt.
I do, however, love Web 3.
Enough Web3 bashing for now. Understand? Decentralization isn't perfect, but it has huge potential when applied to the right problems.
I see many of the right problems as disrupting big tech's ruthless monopolies. I wrote several years ago about how tokenized blockchains could be used to break big tech's stranglehold on platforms, marketplaces, and social media.
Tokenomics schemes can be used for good and are powerful. Here’s how.
Before the ICO boom, I made a series of predictions about blockchain/crypto's future. It's still true.
Here's where I was then and where I see web3 going:
My 11 Big & Bold Predictions for Blockchain
In the near future, people may wear crypto cash rings or bracelets.
While some governments repress cryptocurrency, others will start to embrace it.
Blockchain will fundamentally alter voting and governance, resulting in a more open election process.
Money freedom will lead to a more geographically open world where people will be more able to leave when there is unrest.
Blockchain will make record keeping significantly easier, eliminating the need for a significant portion of government workers whose sole responsibility is paperwork.
Overrated are smart contracts.

6. Tokens will replace company stocks.
7. Blockchain increases real estate's liquidity, value, and volatility.
8. Healthcare may be most affected.
9. Crypto could end privacy and lead to Minority Report.
10. New companies with network effects will displace incumbents.
11. Soon, people will wear rings or bracelets with crypto cash.
Some have already happened, while others are still possible.
Time will tell if they happen.
And finally:
What will web3 be?
Who will be in charge?
Closing remarks
Hope you enjoyed this web3 dive. There's much more to say, but that's for another day.
We're writing history as we go.
Tech regulation, mergers, Bitcoin surge How will history remember us?
What about web3 and blockchain?
Is this a revolution or a tulip craze?
Remember, actions speak louder than words (share them in the comments).
Your turn.
Sam Hickmann
4 years ago
A quick guide to formatting your text on INTΞGRITY
[06/20/2022 update] We have now implemented a powerful text editor, but you can still use markdown.
Markdown:
Headers
SYNTAX:
# This is a heading 1
## This is a heading 2
### This is a heading 3
#### This is a heading 4
RESULT:
This is a heading 1
This is a heading 2
This is a heading 3
This is a heading 4
Emphasis
SYNTAX:
**This text will be bold**
~~Strikethrough~~
*You **can** combine them*
RESULT:
This text will be italic
This text will be bold
You can combine them
Images
SYNTAX:

RESULT:
Videos
SYNTAX:
https://www.youtube.com/watch?v=7KXGZAEWzn0
RESULT:
Links
SYNTAX:
[Int3grity website](https://www.int3grity.com)
RESULT:
Tweets
SYNTAX:
https://twitter.com/samhickmann/status/1503800505864130561
RESULT:
Blockquotes
SYNTAX:
> Human beings face ever more complex and urgent problems, and their effectiveness in dealing with these problems is a matter that is critical to the stability and continued progress of society. \- Doug Engelbart, 1961
RESULT:
Human beings face ever more complex and urgent problems, and their effectiveness in dealing with these problems is a matter that is critical to the stability and continued progress of society. - Doug Engelbart, 1961
Inline code
SYNTAX:
Text inside `backticks` on a line will be formatted like code.
RESULT:
Text inside backticks on a line will be formatted like code.
Code blocks
SYNTAX:
'''js
function fancyAlert(arg) {
if(arg) {
$.facebox({div:'#foo'})
}
}
'''
RESULT:
function fancyAlert(arg) {
if(arg) {
$.facebox({div:'#foo'})
}
}
Maths
We support LaTex to typeset math. We recommend reading the full documentation on the official website
SYNTAX:
$$[x^n+y^n=z^n]$$
RESULT:
[x^n+y^n=z^n]
Tables
SYNTAX:
| header a | header b |
| ---- | ---- |
| row 1 col 1 | row 1 col 2 |
RESULT:
| header a | header b | header c |
|---|---|---|
| row 1 col 1 | row 1 col 2 | row 1 col 3 |
You might also like

Ivona Hirschi
3 years ago
7 LinkedIn Tips That Will Help in Audience Growth
In 8 months, I doubled my audience with them.

LinkedIn's buzz isn't over.
People dream of social proof every day. They want clients, interesting jobs, and field recognition.
LinkedIn coaches will benefit greatly. Sell learning? Probably. Can you use it?
Consistency has been key in my eight-month study of LinkedIn. However, I'll share seven of my tips. 700 to 4500 people followed me.
1. Communication, communication, communication
LinkedIn is a social network. I like to think of it as a cafe. Here, you can share your thoughts, meet friends, and discuss life and work.
Do not treat LinkedIn as if it were a board for your post-its.
More socializing improves relationships. It's about people, like any network.
Consider interactions. Three main areas:
Respond to criticism left on your posts.
Comment on other people's posts
Start and maintain conversations through direct messages.
Engage people. You spend too much time on Facebook if you only read your wall. Keeping in touch and having meaningful conversations helps build your network.
Every day, start a new conversation to make new friends.
2. Stick with those you admire
Interact thoughtfully.
Choose your contacts. Build your tribe is a term. Respectful networking.
I only had past colleagues, family, and friends in my network at the start of this year. Not business-friendly. Since then, I've sought out people I admire or can learn from.
Finding a few will help you. As they connect you to their networks. Friendships can lead to clients.
Don't underestimate network power. Cafe-style. Meet people at each table. But avoid people who sell SEO, web redesign, VAs, mysterious job opportunities, etc.
3. Share eye-catching infographics
Daily infographics flood LinkedIn. Visuals are popular. Use Canva's free templates if you can't draw them.
Last week's:

It's a fun way to visualize your topic.
You can repost and comment on infographics. Involve your network. I prefer making my own because I build my brand around certain designs.
My friend posted infographics consistently for four months and grew his network to 30,000.
If you start, credit the authors. As you steal someone's work.
4. Invite some friends over.
LinkedIn alone can be lonely. Having a few friends who support your work daily will boost your growth.
I was lucky to be invited to a group of networkers. We share knowledge and advice.
Having a few regulars who can discuss your posts is helpful. It's artificial, but it works and engages others.
Consider who you'd support if they were in your shoes.
You can pay for an engagement group, but you risk supporting unrelated people with rubbish posts.
Help each other out.
5. Don't let your feed or algorithm divert you.
LinkedIn's algorithm is magical.
Which time is best? How fast do you need to comment? Which days are best?
Overemphasize algorithms. Consider the user. No need to worry about the best time.
Remember to spend time on LinkedIn actively. Not passively. That is what Facebook is for.
Surely someone would find a LinkedIn recipe. Don't beat the algorithm yet. Consider your audience.
6. The more personal, the better
Personalization isn't limited to selfies. Share your successes and failures.
The more personality you show, the better.
People relate to others, not theories or quotes. Why should they follow you? Everyone posts the same content?
Consider your friends. What's their appeal?
Because they show their work and identity. It's simple. Medium and Linkedin are your platforms. Find out what works.
You can copy others' hooks and structures. You decide how simple to make it, though.
7. Have fun with those who have various post structures.
I like writing, infographics, videos, and carousels. Because you can:
Repurpose your content!
Out of one blog post I make:
Newsletter
Infographics (positive and negative points of view)
Carousel
Personal stories
Listicle
Create less but more variety. Since LinkedIn posts last 24 hours, you can rotate the same topics for weeks without anyone noticing.
Effective!
The final LI snippet to think about
LinkedIn is about consistency. Some say 15 minutes. If you're serious about networking, spend more time there.
The good news is that it is worth it. The bad news is that it takes time.

Dani Herrera
3 years ago
What prevents companies from disclosing salary information?

Yes, salary details ought to be mentioned in job postings. Recruiters and candidates both agree, so why doesn't it happen?
The short answer is “Unfortunately, it’s not the Recruiter’s decision”. The longer answer is well… A LOT.
Starting in November 2022, NYC employers must include salary ranges in job postings. It should have started in May, but companies balked.
I'm thrilled about salary transparency. This decision will promote fair, inclusive, and equitable hiring practices, and I'm sure other states will follow suit. Good news!
Candidates, recruiters, and ED&I practitioners have advocated for pay transparency for years. Why the opposition?
Let's quickly review why companies have trouble sharing salary bands.
💰 Pay Parity
Many companies and leaders still oppose pay parity. Yes, even in 2022.
💰 Pay Equity
Many companies believe in pay parity and have reviewed their internal processes and systems to ensure equality.
However, Pay Equity affects who gets roles/promotions/salary raises/bonuses and when. Enter the pay gap!
💰Pay Transparency and its impact on Talent Retention
Sharing salary bands with external candidates (and the world) means current employees will have access to that information, which is one of the main reasons companies don't share salary data.
If a company has Pay Parity and Pay Equity issues, they probably have a Pay Transparency policy as well.
Sharing salary information with external candidates without ensuring current employees understand their own salary bands and how promotions/raises are decided could impact talent retention strategies.
This information should help clarify recent conversations.

Katrine Tjoelsen
3 years ago
8 Communication Hacks I Use as a Young Employee
Learn these subtle cues to gain influence.

Hate being ignored?
As a 24-year-old, I struggled at work. Attention-getting tips How to avoid being judged by my size, gender, and lack of wrinkles or gray hair?
I've learned seniority hacks. Influence. Within two years as a product manager, I led a team. I'm a Stanford MBA student.
These communication hacks can make you look senior and influential.
1. Slowly speak
We speak quickly because we're afraid of being interrupted.
When I doubt my ideas, I speak quickly. How can we slow down? Jamie Chapman says speaking slowly saps our energy.
Chapman suggests emphasizing certain words and pausing.
2. Interrupted? Stop the stopper
Someone interrupt your speech?
Don't wait. "May I finish?" No pause needed. Stop interrupting. I first tried this in Leadership Laboratory at Stanford. How quickly I gained influence amazed me.
Next time, try “May I finish?” If that’s not enough, try these other tips from Wendy R.S. O’Connor.
3. Context
Others don't always see what's obvious to you.
Through explanation, you help others see the big picture. If a senior knows it, you help them see where your work fits.
4. Don't ask questions in statements
“Your statement lost its effect when you ended it on a high pitch,” a group member told me. Upspeak, it’s called. I do it when I feel uncertain.
Upspeak loses influence and credibility. Unneeded. When unsure, we can say "I think." We can even ask a proper question.
Someone else's boasting is no reason to be dismissive. As leaders and colleagues, we should listen to our colleagues even if they use this speech pattern.
Give your words impact.
5. Signpost structure
Signposts improve clarity by providing structure and transitions.
Communication coach Alexander Lyon explains how to use "first," "second," and "third" He explains classic and summary transitions to help the listener switch topics.
Signs clarify. Clarity matters.

6. Eliminate email fluff
“Fine. When will the report be ready? — Jeff.”
Notice how senior leaders write short, direct emails? I often use formalities like "dear," "hope you're well," and "kind regards"
Formality is (usually) unnecessary.
7. Replace exclamation marks with periods
See how junior an exclamation-filled email looks:
Hi, all!
Hope you’re as excited as I am for tomorrow! We’re celebrating our accomplishments with cake! Join us tomorrow at 2 pm!
See you soon!
Why the exclamation points? Why not just one?
Hi, all.
Hope you’re as excited as I am for tomorrow. We’re celebrating our accomplishments with cake. Join us tomorrow at 2 pm!
See you soon.
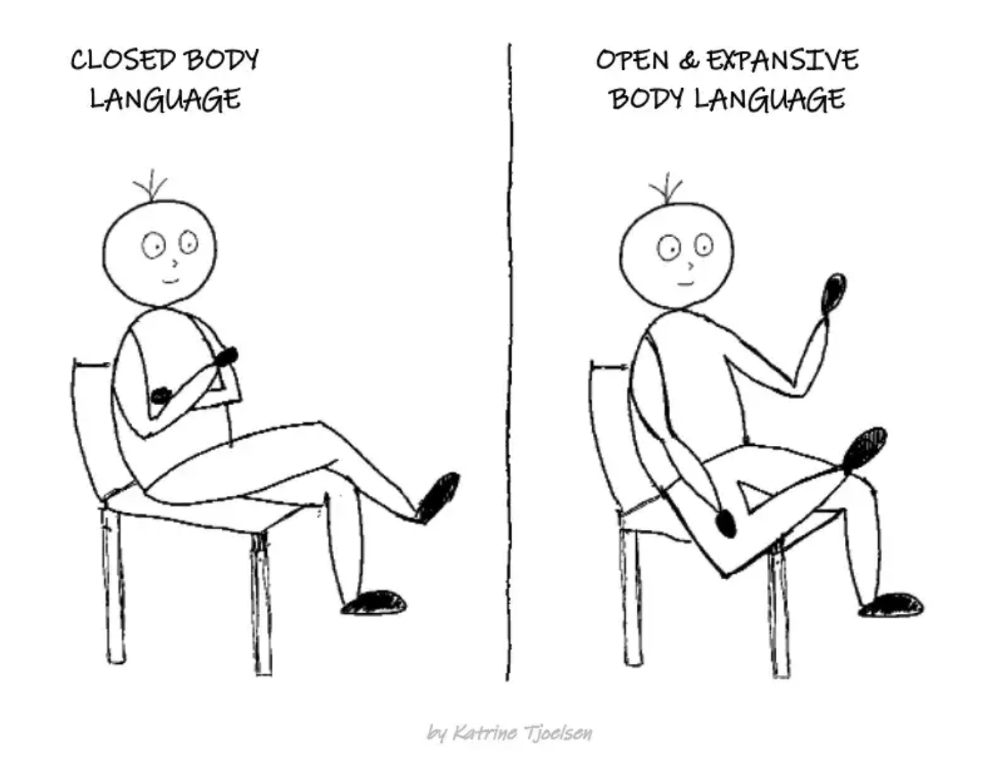
8. Take space
"Playing high" means having an open, relaxed body, says Stanford professor and author Deborah Gruenfield.
Crossed legs or looking small? Relax. Get bigger.