More on Personal Growth

Entreprogrammer
3 years ago
The Steve Jobs Formula: A Guide to Everything
A must-read for everyone

Jobs is well-known. You probably know the tall, thin guy who wore the same clothing every day. His influence is unavoidable. In fewer than 40 years, Jobs' innovations have impacted computers, movies, cellphones, music, and communication.
Steve Jobs may be more imaginative than the typical person, but if we can use some of his ingenuity, ambition, and good traits, we'll be successful. This essay explains how to follow his guidance and success secrets.
1. Repetition is necessary for success.
Be patient and diligent to master something. Practice makes perfect. This is why older workers are often more skilled.
When should you repeat a task? When you're confident and excited to share your product. It's when to stop tweaking and repeating.
Jobs stated he'd make the crowd sh** their pants with an iChat demo.
Use this in your daily life.
Start with the end in mind. You can put it in writing and be as detailed as you like with your plan's schedule and metrics. For instance, you have a goal of selling three coffee makers in a week.
Break it down, break the goal down into particular tasks you must complete, and then repeat those tasks. To sell your coffee maker, you might need to make 50 phone calls.
Be mindful of the amount of work necessary to produce the desired results. Continue doing this until you are happy with your product.
2. Acquire the ability to add and subtract.
How did Picasso invent cubism? Pablo Picasso was influenced by stylised, non-naturalistic African masks that depict a human figure.
Artists create. Constantly seeking inspiration. They think creatively about random objects. Jobs said creativity is linking things. Creative people feel terrible when asked how they achieved something unique because they didn't do it all. They saw innovation. They had mastered connecting and synthesizing experiences.
Use this in your daily life.
On your phone, there is a note-taking app. Ideas for what you desire to learn should be written down. It may be learning a new language, calligraphy, or anything else that inspires or intrigues you.
Note any ideas you have, quotations, or any information that strikes you as important.
Spend time with smart individuals, that is the most important thing. Jim Rohn, a well-known motivational speaker, has observed that we are the average of the five people with whom we spend the most time.
Learning alone won't get you very far. You need to put what you've learnt into practice. If you don't use your knowledge and skills, they are useless.
3. Develop the ability to refuse.
Steve Jobs deleted thousands of items when he created Apple's design ethic. Saying no to distractions meant upsetting customers and partners.
John Sculley, the former CEO of Apple, said something like this. According to Sculley, Steve’s methodology differs from others as he always believed that the most critical decisions are things you choose not to do.
Use this in your daily life.
Never be afraid to say "no," "I won't," or "I don't want to." Keep it simple. This method works well in some situations.
Give a different option. For instance, X might be interested even if I won't be able to achieve it.
Control your top priority. Before saying yes to anything, make sure your work schedule and priority list are up to date.
4. Follow your passion
“Follow your passion” is the worst advice people can give you. Steve Jobs didn't start Apple because he suddenly loved computers. He wanted to help others attain their maximum potential.
Great things take a lot of work, so quitting makes sense if you're not passionate. Jobs learned from history that successful people were passionate about their work and persisted through challenges.
Use this in your daily life.
Stay away from your passion. Allow it to develop daily. Keep working at your 9-5-hour job while carefully gauging your level of desire and endurance. Less risk exists.
The truth is that if you decide to work on a project by yourself rather than in a group, it will take you years to complete it instead of a week. Instead, network with others who have interests in common.
Prepare a fallback strategy in case things go wrong.
Success, this small two-syllable word eventually gives your life meaning, a perspective. What is success? For most, it's achieving their ambitions. However, there's a catch. Successful people aren't always happy.
Furthermore, where do people’s goals and achievements end? It’s a never-ending process. Success is a journey, not a destination. We wish you not to lose your way on this journey.
Matthew Royse
3 years ago
Ten words and phrases to avoid in presentations
Don't say this in public!

Want to wow your audience? Want to deliver a successful presentation? Do you want practical takeaways from your presentation?
Then avoid these phrases.
Public speaking is difficult. People fear public speaking, according to research.
"Public speaking is people's biggest fear, according to studies. Number two is death. "Sounds right?" — Comedian Jerry Seinfeld
Yes, public speaking is scary. These words and phrases will make your presentation harder.
Using unnecessary words can weaken your message.
You may have prepared well for your presentation and feel confident. During your presentation, you may freeze up. You may blank or forget.
Effective delivery is even more important than skillful public speaking.
Here are 10 presentation pitfalls.
1. I or Me
Presentations are about the audience, not you. Replace "I or me" with "you, we, or us." Focus on your audience. Reward them with expertise and intriguing views about your issue.
Serve your audience actionable items during your presentation, and you'll do well. Your audience will have a harder time listening and engaging if you're self-centered.
2. Sorry if/for
Your presentation is fine. These phrases make you sound insecure and unprepared. Don't pressure the audience to tell you not to apologize. Your audience should focus on your presentation and essential messages.
3. Excuse the Eye Chart, or This slide's busy
Why add this slide if you're utilizing these phrases? If you don't like this slide, change it before presenting. After the presentation, extra data can be provided.
Don't apologize for unclear slides. Hide or delete a broken PowerPoint slide. If so, divide your message into multiple slides or remove the "business" slide.
4. Sorry I'm Nervous
Some think expressing yourself will win over the audience. Nerves are horrible. Even public speakers are nervous.
Nerves aren't noticeable. What's the point? Let the audience judge your nervousness. Please don't make this obvious.
5. I'm not a speaker or I've never done this before.
These phrases destroy credibility. People won't listen and will check their phones or computers.
Why present if you use these phrases?
Good speakers aren't necessarily public speakers. Be confident in what you say. When you're confident, many people will like your presentation.
6. Our Key Differentiators Are
Overused term. It's widely utilized. This seems "salesy," and your "important differentiators" are probably like a competitor's.
This statement has been diluted; say, "what makes us different is..."
7. Next Slide
Many slides or stories? Your presentation needs transitions. They help your viewers understand your argument.
You didn't transition well when you said "next slide." Think about organic transitions.
8. I Didn’t Have Enough Time, or I’m Running Out of Time
The phrase "I didn't have enough time" implies that you didn't care about your presentation. This shows the viewers you rushed and didn't care.
Saying "I'm out of time" shows poor time management. It means you didn't rehearse enough and plan your time well.
9. I've been asked to speak on
This phrase is used to emphasize your importance. This phrase conveys conceit.
When you say this sentence, you tell others you're intelligent, skilled, and appealing. Don't utilize this term; focus on your topic.
10. Moving On, or All I Have
These phrases don't consider your transitions or presentation's end. People recall a presentation's beginning and end.
How you end your discussion affects how people remember it. You must end your presentation strongly and use natural transitions.
Conclusion
10 phrases to avoid in a presentation. I or me, sorry if or sorry for, pardon the Eye Chart or this busy slide, forgive me if I appear worried, or I'm really nervous, and I'm not good at public speaking, I'm not a speaker, or I've never done this before.
Please don't use these phrases: next slide, I didn't have enough time, I've been asked to speak about, or that's all I have.
We shouldn't make public speaking more difficult than it is. We shouldn't exacerbate a difficult issue. Better public speakers avoid these words and phrases.
“Remember not only to say the right thing in the right place, but far more difficult still, to leave unsaid the wrong thing at the tempting moment.” — Benjamin Franklin, Founding Father
This is a summary. See the original post here.

Jari Roomer
3 years ago
10 Alternatives to Smartphone Scrolling
"Don't let technology control you; manage your phone."
"Don't become a slave to technology," said Richard Branson. "Manage your phone, don't let it manage you."
Unfortunately, most people are addicted to smartphones.
Worrying smartphone statistics:
46% of smartphone users spend 5–6 hours daily on their device.
The average adult spends 3 hours 54 minutes per day on mobile devices.
We check our phones 150–344 times per day (every 4 minutes).
During the pandemic, children's daily smartphone use doubled.
Having a list of productive, healthy, and fulfilling replacement activities is an effective way to reduce smartphone use.
The more you practice these smartphone replacements, the less time you'll waste.
Skills Development
Most people say they 'don't have time' to learn new skills or read more. Lazy justification. The issue isn't time, but time management. Distractions and low-quality entertainment waste hours every day.
The majority of time is spent in low-quality ways, according to Richard Koch, author of The 80/20 Principle.
What if you swapped daily phone scrolling for skill-building?
There are dozens of skills to learn, from high-value skills to make more money to new languages and party tricks.
Learning a new skill will last for years, if not a lifetime, compared to scrolling through your phone.
Watch Docs
Love documentaries. It's educational and relaxing. A good documentary helps you understand the world, broadens your mind, and inspires you to change.
Recent documentaries I liked include:
14 Peaks: Nothing Is Impossible
The Social Dilemma
Jim & Andy: The Great Beyond
Fantastic Fungi
Make money online
If you've ever complained about not earning enough money, put away your phone and get to work.
Instead of passively consuming mobile content, start creating it. Create something worthwhile. Freelance.
Internet makes starting a business or earning extra money easier than ever.
(Grand)parents didn't have this. Someone made them work 40+ hours. Few alternatives existed.
Today, all you need is internet and a monetizable skill. Use the internet instead of letting it distract you. Profit from it.
Bookworm
Jack Canfield, author of Chicken Soup For The Soul, said, "Everyone spends 2–3 hours a day watching TV." If you read that much, you'll be in the top 1% of your field."
Few people have more than two hours per day to read.
If you read 15 pages daily, you'd finish 27 books a year (as the average non-fiction book is about 200 pages).
Jack Canfield's quote remains relevant even though 15 pages can be read in 20–30 minutes per day. Most spend this time watching TV or on their phones.
What if you swapped 20 minutes of mindless scrolling for reading? You'd gain knowledge and skills.
Favorite books include:
The 7 Habits of Highly Effective People — Stephen R. Covey
The War of Art — Steven Pressfield
The Psychology of Money — Morgan Housel
A New Earth — Eckart Tolle
Get Organized
All that screen time could've been spent organizing. It could have been used to clean, cook, or plan your week.
If you're always 'behind,' spend 15 minutes less on your phone to get organized.
"Give me six hours to chop down a tree, and I'll spend the first four sharpening the ax," said Abraham Lincoln. Getting organized is like sharpening an ax, making each day more efficient.
Creativity
Why not be creative instead of consuming others'? Do something creative, like:
Painting
Musically
Photography\sWriting
Do-it-yourself
Construction/repair
Creative projects boost happiness, cognitive functioning, and reduce stress and anxiety. Creative pursuits induce a flow state, a powerful mental state.
This contrasts with smartphones' effects. Heavy smartphone use correlates with stress, depression, and anxiety.
Hike
People spend 90% of their time indoors, according to research. This generation is the 'Indoor Generation'
We lack an active lifestyle, fresh air, and vitamin D3 due to our indoor lifestyle (generated through direct sunlight exposure). Mental and physical health issues result.
Put away your phone and get outside. Go on nature walks. Explore your city on foot (or by bike, as we do in Amsterdam) if you live in a city. Move around! Outdoors!
You can't spend your whole life staring at screens.
Podcasting
Okay, a smartphone is needed to listen to podcasts. When you use your phone to get smarter, you're more productive than 95% of people.
Favorite podcasts:
The Pomp Podcast (about cryptocurrencies)
The Joe Rogan Experience
Kwik Brain (by Jim Kwik)
Podcasts can be enjoyed while walking, cleaning, or doing laundry. Win-win.
Journalize
I find journaling helpful for mental clarity. Writing helps organize thoughts.
Instead of reading internet opinions, comments, and discussions, look inward. Instead of Twitter or TikTok, look inward.
“It never ceases to amaze me: we all love ourselves more than other people, but care more about their opinion than our own.” — Marcus Aurelius
Give your mind free reign with pen and paper. It will highlight important thoughts, emotions, or ideas.
Never write for another person. You want unfiltered writing. So you get the best ideas.
Find your best hobbies
List your best hobbies. I guarantee 95% of people won't list smartphone scrolling.
It's often low-quality entertainment. The dopamine spike is short-lived, and it leaves us feeling emotionally 'empty'
High-quality leisure sparks happiness. They make us happy and alive. Everyone has different interests, so these activities vary.
My favorite quality hobbies are:
Nature walks (especially the mountains)
Video game party
Watching a film with my girlfriend
Gym weightlifting
Complexity learning (such as the blockchain and the universe)
This brings me joy. They make me feel more fulfilled and 'rich' than social media scrolling.
Make a list of your best hobbies to refer to when you're spending too much time on your phone.
You might also like

Aaron Dinin, PhD
2 years ago
Are You Unintentionally Creating the Second Difficult Startup Type?
Most don't understand the issue until it's too late.

My first startup was what entrepreneurs call the hardest. A two-sided marketplace.
Two-sided marketplaces are the hardest startups because founders must solve the chicken or the egg conundrum.
A two-sided marketplace needs suppliers and buyers. Without suppliers, buyers won't come. Without buyers, suppliers won't come. An empty marketplace and a founder striving to gain momentum result.
My first venture made me a struggling founder seeking to achieve traction for a two-sided marketplace. The company failed, and I vowed never to start another like it.
I didn’t. Unfortunately, my second venture was almost as hard. It failed like the second-hardest startup.
What kind of startup is the second-hardest?
The second-hardest startup, which is almost as hard to develop, is rarely discussed in the startup community. Because of this, I predict more founders fail each year trying to develop the second-toughest startup than the hardest.
Fairly, I have no proof. I see many startups, so I have enough of firsthand experience. From what I've seen, for every entrepreneur developing a two-sided marketplace, I'll meet at least 10 building this other challenging startup.
I'll describe a startup I just met with its two co-founders to explain the second hardest sort of startup and why it's so hard. They created a financial literacy software for parents of high schoolers.
The issue appears plausible. Children struggle with money. Parents must teach financial responsibility. Problems?
It's possible.
Buyers and users are different.
Buyer-user mismatch.
The financial literacy app I described above targets parents. The parent doesn't utilize the app. Child is end-user. That may not seem like much, but it makes customer and user acquisition and onboarding difficult for founders.
The difficulty of a buyer-user imbalance
The company developing a product faces a substantial operational burden when the buyer and end customer are different. Consider classic firms where the buyer is the end user to appreciate that responsibility.
Entrepreneurs selling directly to end users must educate them about the product's benefits and use. Each demands a lot of time, effort, and resources.
Imagine selling a financial literacy app where the buyer and user are different. To make the first sale, the entrepreneur must establish all the items I mentioned above. After selling, the entrepreneur must supply a fresh set of resources to teach, educate, or train end-users.
Thus, a startup with a buyer-user mismatch must market, sell, and train two organizations at once, requiring twice the work with the same resources.
The second hardest startup is hard for reasons other than the chicken-or-the-egg conundrum. It takes a lot of creativity and luck to solve the chicken-or-egg conundrum.
The buyer-user mismatch problem cannot be overcome by innovation or luck. Buyer-user mismatches must be solved by force. Simply said, when a product buyer is different from an end-user, founders have a lot more work. If they can't work extra, their companies fail.

Shalitha Suranga
3 years ago
The Top 5 Mathematical Concepts Every Programmer Needs to Know
Using math to write efficient code in any language

Programmers design, build, test, and maintain software. Employ cases and personal preferences determine the programming languages we use throughout development. Mobile app developers use JavaScript or Dart. Some programmers design performance-first software in C/C++.
A generic source code includes language-specific grammar, pre-implemented function calls, mathematical operators, and control statements. Some mathematical principles assist us enhance our programming and problem-solving skills.
We all use basic mathematical concepts like formulas and relational operators (aka comparison operators) in programming in our daily lives. Beyond these mathematical syntaxes, we'll see discrete math topics. This narrative explains key math topics programmers must know. Master these ideas to produce clean and efficient software code.
Expressions in mathematics and built-in mathematical functions
A source code can only contain a mathematical algorithm or prebuilt API functions. We develop source code between these two ends. If you create code to fetch JSON data from a RESTful service, you'll invoke an HTTP client and won't conduct any math. If you write a function to compute the circle's area, you conduct the math there.
When your source code gets more mathematical, you'll need to use mathematical functions. Every programming language has a math module and syntactical operators. Good programmers always consider code readability, so we should learn to write readable mathematical expressions.
Linux utilizes clear math expressions.
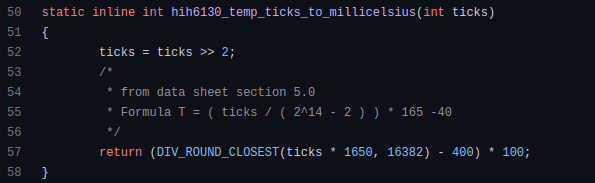
Inbuilt max and min functions can minimize verbose if statements.
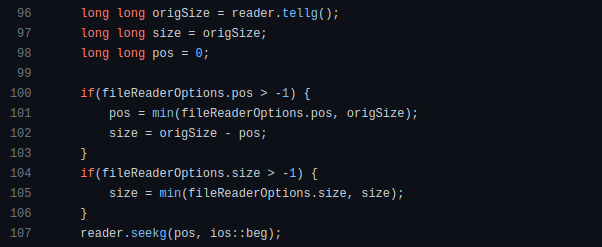
How can we compute the number of pages needed to display known data? In such instances, the ceil function is often utilized.
import math as m
results = 102
items_per_page = 10
pages = m.ceil(results / items_per_page)
print(pages)Learn to write clear, concise math expressions.
Combinatorics in Algorithm Design
Combinatorics theory counts, selects, and arranges numbers or objects. First, consider these programming-related questions. Four-digit PIN security? what options exist? What if the PIN has a prefix? How to locate all decimal number pairs?
Combinatorics questions. Software engineering jobs often require counting items. Combinatorics counts elements without counting them one by one or through other verbose approaches, therefore it enables us to offer minimum and efficient solutions to real-world situations. Combinatorics helps us make reliable decision tests without missing edge cases. Write a program to see if three inputs form a triangle. This is a question I commonly ask in software engineering interviews.
Graph theory is a subfield of combinatorics. Graph theory is used in computerized road maps and social media apps.
Logarithms and Geometry Understanding
Geometry studies shapes, angles, and sizes. Cartesian geometry involves representing geometric objects in multidimensional planes. Geometry is useful for programming. Cartesian geometry is useful for vector graphics, game development, and low-level computer graphics. We can simply work with 2D and 3D arrays as plane axes.
GetWindowRect is a Windows GUI SDK geometric object.
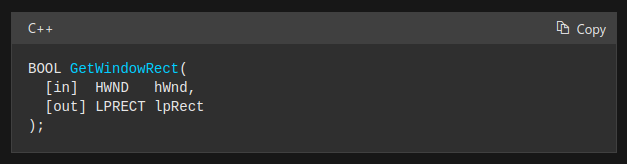
High-level GUI SDKs and libraries use geometric notions like coordinates, dimensions, and forms, therefore knowing geometry speeds up work with computer graphics APIs.
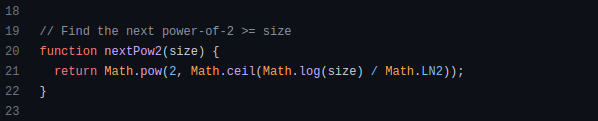
How does exponentiation's inverse function work? Logarithm is exponentiation's inverse function. Logarithm helps programmers find efficient algorithms and solve calculations. Writing efficient code involves finding algorithms with logarithmic temporal complexity. Programmers prefer binary search (O(log n)) over linear search (O(n)). Git source specifies O(log n):
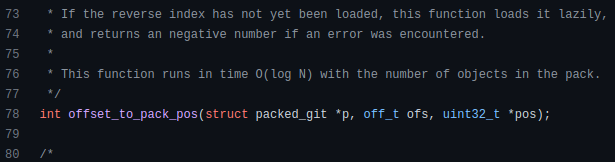
Logarithms aid with programming math. Metas Watchman uses a logarithmic utility function to find the next power of two.
Employing Mathematical Data Structures
Programmers must know data structures to develop clean, efficient code. Stack, queue, and hashmap are computer science basics. Sets and graphs are discrete arithmetic data structures. Most computer languages include a set structure to hold distinct data entries. In most computer languages, graphs can be represented using neighboring lists or objects.
Using sets as deduped lists is powerful because set implementations allow iterators. Instead of a list (or array), store WebSocket connections in a set.
Most interviewers ask graph theory questions, yet current software engineers don't practice algorithms. Graph theory challenges become obligatory in IT firm interviews.
Recognizing Applications of Recursion
A function in programming isolates input(s) and output(s) (s). Programming functions may have originated from mathematical function theories. Programming and math functions are different but similar. Both function types accept input and return value.
Recursion involves calling the same function inside another function. In its implementation, you'll call the Fibonacci sequence. Recursion solves divide-and-conquer software engineering difficulties and avoids code repetition. I recently built the following recursive Dart code to render a Flutter multi-depth expanding list UI:
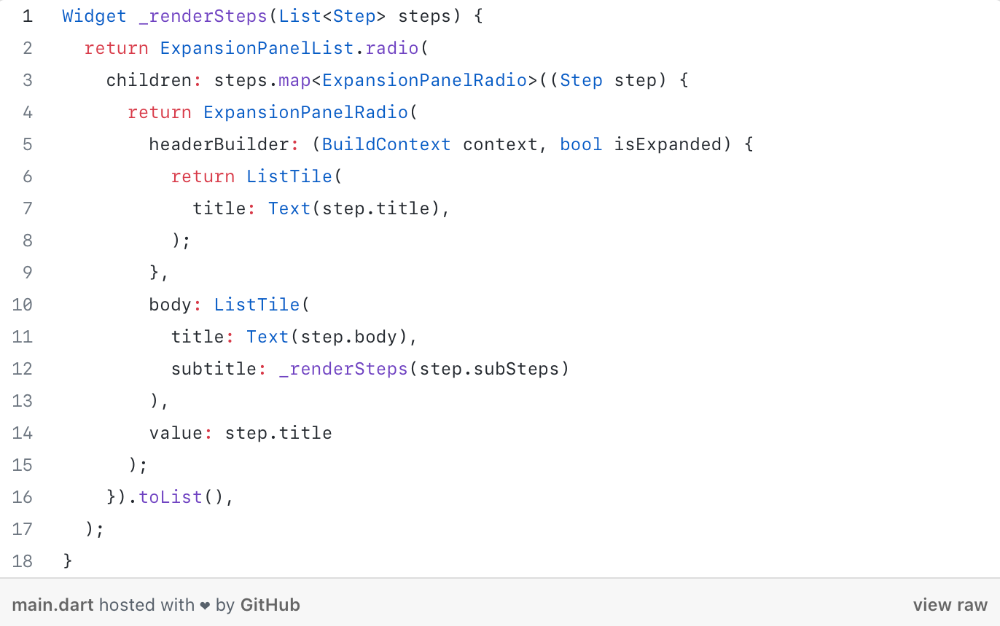
Recursion is not the natural linear way to solve problems, hence thinking recursively is difficult. Everything becomes clear when a mathematical function definition includes a base case and recursive call.
Conclusion
Every codebase uses arithmetic operators, relational operators, and expressions. To build mathematical expressions, we typically employ log, ceil, floor, min, max, etc. Combinatorics, geometry, data structures, and recursion help implement algorithms. Unless you operate in a pure mathematical domain, you may not use calculus, limits, and other complex math in daily programming (i.e., a game engine). These principles are fundamental for daily programming activities.
Master the above math fundamentals to build clean, efficient code.

Michael Le
3 years ago
Union LA x Air Jordan 2 “Future Is Now” PREVIEW
With the help of Virgil Abloh and Union LA‘s Chris Gibbs, it's now clear that Jordan Brand intended to bring the Air Jordan 2 back in 2022.
The “Future Is Now” collection includes two colorways of MJ's second signature as well as an extensive range of apparel and accessories.
“We wanted to juxtapose what some futuristic gear might look like after being worn and patina'd,”
Union stated on the collaboration's landing page.
“You often see people's future visions that are crisp and sterile. We thought it would be cool to wear it in and make it organic...”
The classic co-branding appears on short-sleeve tees, hoodies, and sweat shorts/sweat pants, all lightly distressed at the hems and seams.
Also, a filtered black-and-white photo of MJ graces the adjacent long sleeves, labels stitch into the socks, and the Jumpman logo adorns the four caps.
Liner jackets and flight pants will also be available, adding reimagined militaria to a civilian ensemble.
The Union LA x Air Jordan 2 (Grey Fog and Rattan) shares many of the same beats. Vintage suedes show age, while perforations and detailing reimagine Bruce Kilgore's design for the future.
The “UN/LA” tag across the modified eye stays, the leather patch across the tongue, and the label that wraps over the lateral side of the collar complete the look.
The footwear will also include a Crater Slide in the “Grey Fog” color scheme.
BUYING
On 4/9 and 4/10 from 9am-3pm, Union LA will be giving away a pair of Air Jordan 2s at their La Brea storefront (110 S. LA BREA AVE. LA, CA 90036). The raffle is only open to LA County residents with a valid CA ID. You must enter by 11:59pm on 4/10 to win. Winners will be notified via email.
