More on Entrepreneurship/Creators

Alex Mathers
3 years ago
400 articles later, nobody bothered to read them.
Writing for readers:
14 years of daily writing.
I post practically everything on social media. I authored hundreds of articles, thousands of tweets, and numerous volumes to almost no one.
Tens of thousands of readers regularly praise me.
I despised writing. I'm stuck now.
I've learned what readers like and what doesn't.
Here are some essential guidelines for writing with impact:
Readers won't understand your work if you can't.
Though obvious, this slipped me up. Share your truths.
Stories engage human brains.
Showing the journey of a person from worm to butterfly inspires the human spirit.
Overthinking hinders powerful writing.
The best ideas come from inner understanding in between thoughts.
Avoid writing to find it. Write.
Writing a masterpiece isn't motivating.
Write for five minutes to simplify. Step-by-step, entertaining, easy steps.
Good writing requires a willingness to make mistakes.
So write loads of garbage that you can edit into a good piece.
Courageous writing.
A courageous story will move readers. Personal experience is best.
Go where few dare.
Templates, outlines, and boundaries help.
Limitations enhance writing.
Excellent writing is straightforward and readable, removing all the unnecessary fat.
Use five words instead of nine.
Use ordinary words instead of uncommon ones.
Readers desire relatability.
Too much perfection will turn it off.
Write to solve an issue if you can't think of anything to write.
Instead, read to inspire. Best authors read.
Every tweet, thread, and novel must have a central idea.
What's its point?
This can make writing confusing.
️ Don't direct your reader.
Readers quit reading. Demonstrate, describe, and relate.
Even if no one responds, have fun. If you hate writing it, the reader will too.

Antonio Neto
3 years ago
Should you skip the minimum viable product?
Are MVPs outdated and have no place in modern product culture?

Frank Robinson coined "MVP" in 2001. In the same year as the Agile Manifesto, the first Scrum experiment began. MVPs are old.
The concept was created to solve the waterfall problem at the time.
The market was still sour from the .com bubble. The tech industry needed a new approach. Product and Agile gained popularity because they weren't waterfall.
More than 20 years later, waterfall is dead as dead can be, but we are still talking about MVPs. Does that make sense?
What is an MVP?
Minimum viable product. You probably know that, so I'll be brief:
[…] The MVP fits your company and customer. It's big enough to cause adoption, satisfaction, and sales, but not bloated and risky. It's the product with the highest ROI/risk. […] — Frank Robinson, SyncDev
MVP is a complete product. It's not a prototype. It's your product's first iteration, which you'll improve. It must drive sales and be user-friendly.
At the MVP stage, you should know your product's core value, audience, and price. We are way deep into early adoption territory.
What about all the things that come before?
Modern product discovery
Eric Ries popularized the term with The Lean Startup in 2011. (Ries would work with the concept since 2008, but wide adoption came after the book was released).
Ries' definition of MVP was similar to Robinson's: "Test the market" before releasing anything. Ries never mentioned money, unlike Jobs. His MVP's goal was learning.
“Remove any feature, process, or effort that doesn't directly contribute to learning” — Eric Ries, The Lean Startup
Product has since become more about "what" to build than building it. What started as a learning tool is now a discovery discipline: fake doors, prototyping, lean inception, value proposition canvas, continuous interview, opportunity tree... These are cheap, effective learning tools.
Over time, companies realized that "maximum ROI divided by risk" started with discovery, not the MVP. MVPs are still considered discovery tools. What is the problem with that?
Time to Market vs Product Market Fit
Waterfall's Time to Market is its biggest flaw. Since projects are sliced horizontally rather than vertically, when there is nothing else to be done, it’s not because the product is ready, it’s because no one cares to buy it anymore.
MVPs were originally conceived as a way to cut corners and speed Time to Market by delivering more customer requests after they paid.
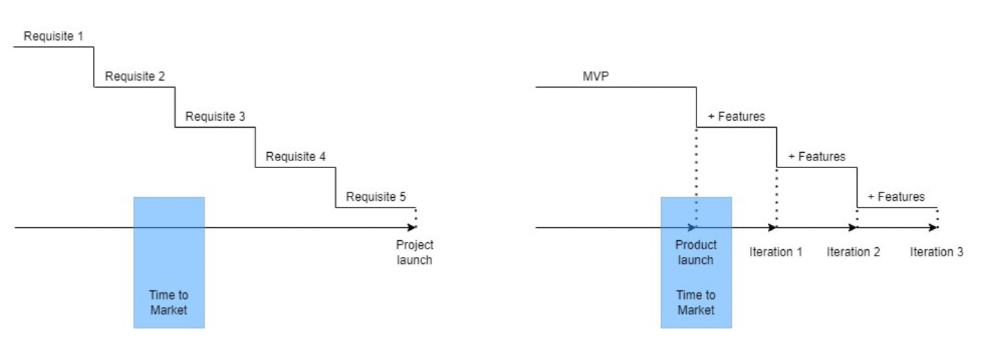
Original product development was waterfall-like.
Time to Market defines an optimal, specific window in which value should be delivered. It's impossible to predict how long or how often this window will be open.
Product Market Fit makes this window a "state." You don’t achieve Product Market Fit, you have it… and you may lose it.
Take, for example, Snapchat. They had a great time to market, but lost product-market fit later. They regained product-market fit in 2018 and have grown since.
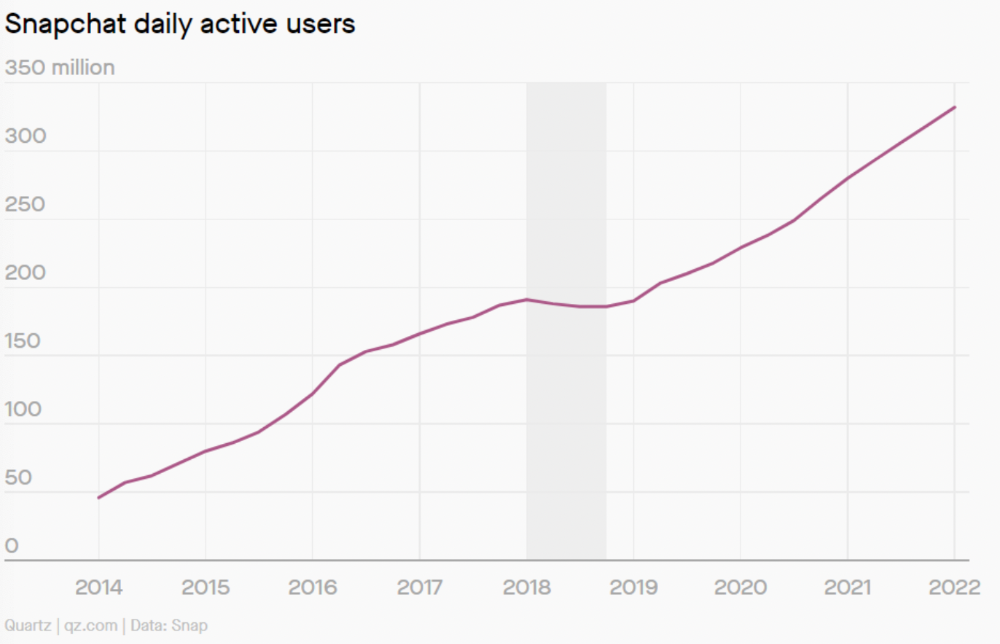
An MVP couldn't handle this. What should Snapchat do? Launch Snapchat 2 and see what the market was expecting differently from the last time? MVPs are a snapshot in time that may be wrong in two weeks.
MVPs are mini-projects. Instead of spending a lot of time and money on waterfall, you spend less but are still unsure of the results.
MVPs aren't always wrong. When releasing your first product version, consider an MVP.
Minimum viable product became less of a thing on its own and more interchangeable with Alpha Release or V.1 release over time.
Modern discovery technics are more assertive and predictable than the MVP, but clarity comes only when you reach the market.
MVPs aren't the starting point, but they're the best way to validate your product concept.

Kaitlin Fritz
3 years ago
The Entrepreneurial Chicken and Egg
University entrepreneurship is like a Willy Wonka Factory of ideas. Classes, roommates, discussions, and the cafeteria all inspire new ideas. I've seen people establish a business without knowing its roots.
Chicken or egg? On my mind: I've asked university founders around the world whether the problem or solution came first.
The Problem
One African team I met started with the “instant noodles” problem in their academic ecosystem. Many of us have had money issues in college, which may have led to poor nutritional choices.
Many university students in a war-torn country ate quick noodles or pasta for dinner.

Noodles required heat, water, and preparation in the boarding house. Unreliable power from one hot plate per blue moon. What's healthier, easier, and tastier than sodium-filled instant pots?
BOOM. They were fixing that. East African kids need affordable, nutritious food.
This is a real difficulty the founders faced every day with hundreds of comrades.
This sparked their serendipitous entrepreneurial journey and became their business's cornerstone.
The Solution
I asked a UK team about their company idea. They said the solution fascinated them.
The crew was fiddling with social media algorithms. Why are some people more popular? They were studying platforms and social networks, which offered a way for them.

Solving a problem? Yes. Long nights of university research lead them to it. Is this like world hunger? Social media influencers confront this difficulty regularly.
It made me ponder something. Is there a correct response?
In my heart, yes, but in my head…maybe?
I believe you should lead with empathy and embrace the problem, not the solution. Big or small, businesses should solve problems. This should be your focus. This is especially true when building a social company with an audience in mind.
Philosophically, invention and innovation are occasionally accidental. Also not penalized. Think about bugs and the creation of Velcro, or the inception of Teflon. They tackle difficulties we overlook. The route to the problem may look different, but there is a path there.
There's no golden ticket to the Chicken-Egg debate, but I'll keep looking this summer.
You might also like

Farhan Ali Khan
2 years ago
Introduction to Zero-Knowledge Proofs: The Art of Proving Without Revealing
Zero-Knowledge Proofs for Beginners
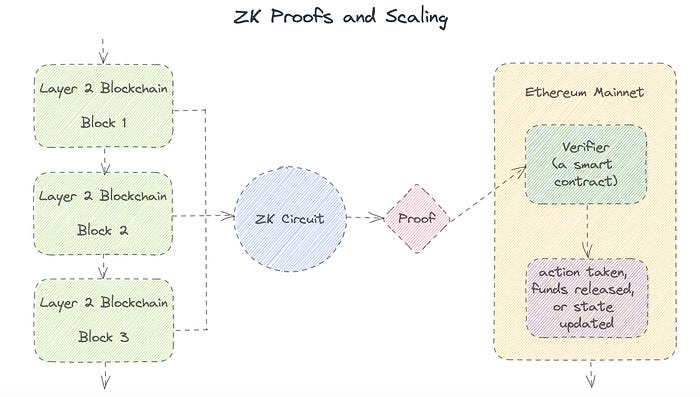
Published here originally.
Introduction
I Spy—did you play as a kid? One person chose a room object, and the other had to guess it by answering yes or no questions. I Spy was entertaining, but did you know it could teach you cryptography?
Zero Knowledge Proofs let you show your pal you know what they picked without exposing how. Math replaces electronics in this secret spy mission. Zero-knowledge proofs (ZKPs) are sophisticated cryptographic tools that allow one party to prove they have particular knowledge without revealing it. This proves identification and ownership, secures financial transactions, and more. This article explains zero-knowledge proofs and provides examples to help you comprehend this powerful technology.
What is a Proof of Zero Knowledge?
Zero-knowledge proofs prove a proposition is true without revealing any other information. This lets the prover show the verifier that they know a fact without revealing it. So, a zero-knowledge proof is like a magician's trick: the prover proves they know something without revealing how or what. Complex mathematical procedures create a proof the verifier can verify.
Want to find an easy way to test it out? Try out with tis awesome example! ZK Crush
Describe it as if I'm 5
Alex and Jack found a cave with a center entrance that only opens when someone knows the secret. Alex knows how to open the cave door and wants to show Jack without telling him.
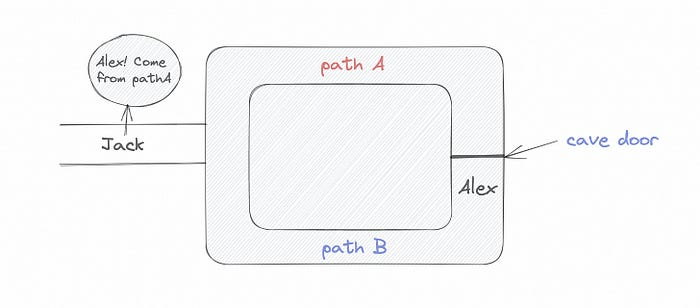
Alex and Jack name both pathways (let’s call them paths A and B).
In the first phase, Alex is already inside the cave and is free to select either path, in this case A or B.
As Alex made his decision, Jack entered the cave and asked him to exit from the B path.
Jack can confirm that Alex really does know the key to open the door because he came out for the B path and used it.
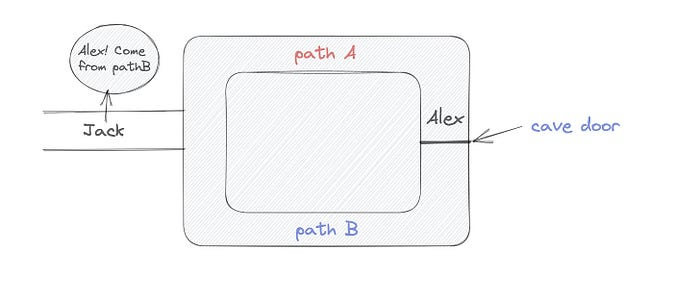
To conclude, Alex and Jack repeat:
Alex walks into the cave.
Alex follows a random route.
Jack walks into the cave.
Alex is asked to follow a random route by Jack.
Alex follows Jack's advice and heads back that way.
What is a Zero Knowledge Proof?
At a high level, the aim is to construct a secure and confidential conversation between the prover and the verifier, where the prover convinces the verifier that they have the requisite information without disclosing it. The prover and verifier exchange messages and calculate in each round of the dialogue.
The prover uses their knowledge to prove they have the information the verifier wants during these rounds. The verifier can verify the prover's truthfulness without learning more by checking the proof's mathematical statement or computation.
Zero knowledge proofs use advanced mathematical procedures and cryptography methods to secure communication. These methods ensure the evidence is authentic while preventing the prover from creating a phony proof or the verifier from extracting unnecessary information.
ZK proofs require examples to grasp. Before the examples, there are some preconditions.
Criteria for Proofs of Zero Knowledge
Completeness: If the proposition being proved is true, then an honest prover will persuade an honest verifier that it is true.
Soundness: If the proposition being proved is untrue, no dishonest prover can persuade a sincere verifier that it is true.
Zero-knowledge: The verifier only realizes that the proposition being proved is true. In other words, the proof only establishes the veracity of the proposition being supported and nothing more.
The zero-knowledge condition is crucial. Zero-knowledge proofs show only the secret's veracity. The verifier shouldn't know the secret's value or other details.
Example after example after example
To illustrate, take a zero-knowledge proof with several examples:
Initial Password Verification Example
You want to confirm you know a password or secret phrase without revealing it.
Use a zero-knowledge proof:
You and the verifier settle on a mathematical conundrum or issue, such as figuring out a big number's components.
The puzzle or problem is then solved using the hidden knowledge that you have learned. You may, for instance, utilize your understanding of the password to determine the components of a particular number.
You provide your answer to the verifier, who can assess its accuracy without knowing anything about your private data.
You go through this process several times with various riddles or issues to persuade the verifier that you actually are aware of the secret knowledge.
You solved the mathematical puzzles or problems, proving to the verifier that you know the hidden information. The proof is zero-knowledge since the verifier only sees puzzle solutions, not the secret information.
In this scenario, the mathematical challenge or problem represents the secret, and solving it proves you know it. The evidence does not expose the secret, and the verifier just learns that you know it.
My simple example meets the zero-knowledge proof conditions:
Completeness: If you actually know the hidden information, you will be able to solve the mathematical puzzles or problems, hence the proof is conclusive.
Soundness: The proof is sound because the verifier can use a publicly known algorithm to confirm that your answer to the mathematical conundrum or difficulty is accurate.
Zero-knowledge: The proof is zero-knowledge because all the verifier learns is that you are aware of the confidential information. Beyond the fact that you are aware of it, the verifier does not learn anything about the secret information itself, such as the password or the factors of the number. As a result, the proof does not provide any new insights into the secret.
Explanation #2: Toss a coin.
One coin is biased to come up heads more often than tails, while the other is fair (i.e., comes up heads and tails with equal probability). You know which coin is which, but you want to show a friend you can tell them apart without telling them.
Use a zero-knowledge proof:
One of the two coins is chosen at random, and you secretly flip it more than once.
You show your pal the following series of coin flips without revealing which coin you actually flipped.
Next, as one of the two coins is flipped in front of you, your friend asks you to tell which one it is.
Then, without revealing which coin is which, you can use your understanding of the secret order of coin flips to determine which coin your friend flipped.
To persuade your friend that you can actually differentiate between the coins, you repeat this process multiple times using various secret coin-flipping sequences.
In this example, the series of coin flips represents the knowledge of biased and fair coins. You can prove you know which coin is which without revealing which is biased or fair by employing a different secret sequence of coin flips for each round.
The evidence is zero-knowledge since your friend does not learn anything about which coin is biased and which is fair other than that you can tell them differently. The proof does not indicate which coin you flipped or how many times you flipped it.
The coin-flipping example meets zero-knowledge proof requirements:
Completeness: If you actually know which coin is biased and which is fair, you should be able to distinguish between them based on the order of coin flips, and your friend should be persuaded that you can.
Soundness: Your friend may confirm that you are correctly recognizing the coins by flipping one of them in front of you and validating your answer, thus the proof is sound in that regard. Because of this, your acquaintance can be sure that you are not just speculating or picking a coin at random.
Zero-knowledge: The argument is that your friend has no idea which coin is biased and which is fair beyond your ability to distinguish between them. Your friend is not made aware of the coin you used to make your decision or the order in which you flipped the coins. Consequently, except from letting you know which coin is biased and which is fair, the proof does not give any additional information about the coins themselves.
Figure out the prime number in Example #3.
You want to prove to a friend that you know their product n=pq without revealing p and q. Zero-knowledge proof?
Use a variant of the RSA algorithm. Method:
You determine a new number s = r2 mod n by computing a random number r.
You email your friend s and a declaration that you are aware of the values of p and q necessary for n to equal pq.
A random number (either 0 or 1) is selected by your friend and sent to you.
You send your friend r as evidence that you are aware of the values of p and q if e=0. You calculate and communicate your friend's s/r if e=1.
Without knowing the values of p and q, your friend can confirm that you know p and q (in the case where e=0) or that s/r is a legitimate square root of s mod n (in the situation where e=1).
This is a zero-knowledge proof since your friend learns nothing about p and q other than their product is n and your ability to verify it without exposing any other information. You can prove that you know p and q by sending r or by computing s/r and sending that instead (if e=1), and your friend can verify that you know p and q or that s/r is a valid square root of s mod n without learning anything else about their values. This meets the conditions of completeness, soundness, and zero-knowledge.
Zero-knowledge proofs satisfy the following:
Completeness: The prover can demonstrate this to the verifier by computing q = n/p and sending both p and q to the verifier. The prover also knows a prime number p and a factorization of n as p*q.
Soundness: Since it is impossible to identify any pair of numbers that correctly factorize n without being aware of its prime factors, the prover is unable to demonstrate knowledge of any p and q that do not do so.
Zero knowledge: The prover only admits that they are aware of a prime number p and its associated factor q, which is already known to the verifier. This is the extent of their knowledge of the prime factors of n. As a result, the prover does not provide any new details regarding n's prime factors.
Types of Proofs of Zero Knowledge
Each zero-knowledge proof has pros and cons. Most zero-knowledge proofs are:
Interactive Zero Knowledge Proofs: The prover and the verifier work together to establish the proof in this sort of zero-knowledge proof. The verifier disputes the prover's assertions after receiving a sequence of messages from the prover. When the evidence has been established, the prover will employ these new problems to generate additional responses.
Non-Interactive Zero Knowledge Proofs: For this kind of zero-knowledge proof, the prover and verifier just need to exchange a single message. Without further interaction between the two parties, the proof is established.
A statistical zero-knowledge proof is one in which the conclusion is reached with a high degree of probability but not with certainty. This indicates that there is a remote possibility that the proof is false, but that this possibility is so remote as to be unimportant.
Succinct Non-Interactive Argument of Knowledge (SNARKs): SNARKs are an extremely effective and scalable form of zero-knowledge proof. They are utilized in many different applications, such as machine learning, blockchain technology, and more. Similar to other zero-knowledge proof techniques, SNARKs enable one party—the prover—to demonstrate to another—the verifier—that they are aware of a specific piece of information without disclosing any more information about that information.
The main characteristic of SNARKs is their succinctness, which refers to the fact that the size of the proof is substantially smaller than the amount of the original data being proved. Because to its high efficiency and scalability, SNARKs can be used in a wide range of applications, such as machine learning, blockchain technology, and more.
Uses for Zero Knowledge Proofs
ZKP applications include:
Verifying Identity ZKPs can be used to verify your identity without disclosing any personal information. This has uses in access control, digital signatures, and online authentication.
Proof of Ownership ZKPs can be used to demonstrate ownership of a certain asset without divulging any details about the asset itself. This has uses for protecting intellectual property, managing supply chains, and owning digital assets.
Financial Exchanges Without disclosing any details about the transaction itself, ZKPs can be used to validate financial transactions. Cryptocurrency, internet payments, and other digital financial transactions can all use this.
By enabling parties to make calculations on the data without disclosing the data itself, Data Privacy ZKPs can be used to preserve the privacy of sensitive data. Applications for this can be found in the financial, healthcare, and other sectors that handle sensitive data.
By enabling voters to confirm that their vote was counted without disclosing how they voted, elections ZKPs can be used to ensure the integrity of elections. This is applicable to electronic voting, including internet voting.
Cryptography Modern cryptography's ZKPs are a potent instrument that enable secure communication and authentication. This can be used for encrypted messaging and other purposes in the business sector as well as for military and intelligence operations.
Proofs of Zero Knowledge and Compliance
Kubernetes and regulatory compliance use ZKPs in many ways. Examples:
Security for Kubernetes ZKPs offer a mechanism to authenticate nodes without disclosing any sensitive information, enhancing the security of Kubernetes clusters. ZKPs, for instance, can be used to verify, without disclosing the specifics of the program, that the nodes in a Kubernetes cluster are running permitted software.
Compliance Inspection Without disclosing any sensitive information, ZKPs can be used to demonstrate compliance with rules like the GDPR, HIPAA, and PCI DSS. ZKPs, for instance, can be used to demonstrate that data has been encrypted and stored securely without divulging the specifics of the mechanism employed for either encryption or storage.
Access Management Without disclosing any private data, ZKPs can be used to offer safe access control to Kubernetes resources. ZKPs can be used, for instance, to demonstrate that a user has the necessary permissions to access a particular Kubernetes resource without disclosing the details of those permissions.
Safe Data Exchange Without disclosing any sensitive information, ZKPs can be used to securely transmit data between Kubernetes clusters or between several businesses. ZKPs, for instance, can be used to demonstrate the sharing of a specific piece of data between two parties without disclosing the details of the data itself.
Kubernetes deployments audited Without disclosing the specifics of the deployment or the data being processed, ZKPs can be used to demonstrate that Kubernetes deployments are working as planned. This can be helpful for auditing purposes and for ensuring that Kubernetes deployments are operating as planned.
ZKPs preserve data and maintain regulatory compliance by letting parties prove things without revealing sensitive information. ZKPs will be used more in Kubernetes as it grows.

Boris Müller
3 years ago
Why Do Websites Have the Same Design?
My kids redesigned the internet because it lacks inventiveness.

Internet today is bland. Everything is generic: fonts, layouts, pages, and visual language. Microtypography is messy.
Web design today seems dictated by technical and ideological constraints rather than creativity and ideas. Text and graphics are in containers on every page. All design is assumed.
Ironically, web technologies can design a lot. We can execute most designs. We make shocking, evocative websites. Experimental typography, generating graphics, and interactive experiences are possible.
Even designer websites use containers in containers. Dribbble and Behance, the two most popular creative websites, are boring. Lead image.
How did this happen?
Several reasons. WordPress and other blogging platforms use templates. These frameworks build web pages by combining graphics, headlines, body content, and videos. Not designs, templates. These rules combine related data types. These platforms don't let users customize pages beyond the template. You filled the template.
Templates are content-neutral. Thus, the issue.
Form should reflect and shape content, which is a design principle. Separating them produces content containers. Templates have no design value.
One of the fundamental principles of design is a deep and meaningful connection between form and content.
Web design lacks imagination for many reasons. Most are pragmatic and economic. Page design takes time. Large websites lack the resources to create a page from scratch due to the speed of internet news and the frequency of new items. HTML, JavaScript, and CSS continue to challenge web designers. Web design can't match desktop publishing's straightforward operations.
Designers may also be lazy. Mobile-first, generic, framework-driven development tends to ignore web page visual and contextual integrity.
How can we overcome this? How might expressive and avant-garde websites look today?
Rediscovering the past helps design the future.
'90s-era web design
At the University of the Arts Bremen's research and development group, I created my first website 23 years ago. Web design was trendy. Young web. Pages inspired me.
We struggled with HTML in the mid-1990s. Arial, Times, and Verdana were the only web-safe fonts. Anything exciting required table layouts, monospaced fonts, or GIFs. HTML was originally content-driven, thus we had to work against it to create a page.
Experimental typography was booming. Designers challenged the established quo from Jan Tschichold's Die Neue Typographie in the twenties to April Greiman's computer-driven layouts in the eighties. By the mid-1990s, an uncommon confluence of technological and cultural breakthroughs enabled radical graphic design. Irma Boom, David Carson, Paula Scher, Neville Brody, and others showed it.
Early web pages were dull compared to graphic design's aesthetic explosion. The Web Design Museum shows this.
Nobody knew how to conduct browser-based graphic design. Web page design was undefined. No standards. No CMS (nearly), CSS, JS, video, animation.
Now is as good a time as any to challenge the internet’s visual conformity.
In 2018, everything is browser-based. Massive layouts to micro-typography, animation, and video. How do we use these great possibilities? Containerized containers. JavaScript-contaminated mobile-first pages. Visually uniform templates. Web design 23 years later would disappoint my younger self.
Our imagination, not technology, restricts web design. We're too conformist to aesthetics, economics, and expectations.
Crisis generates opportunity. Challenge online visual conformity now. I'm too old and bourgeois to develop a radical, experimental, and cutting-edge website. I can ask my students.
I taught web design at the Potsdam Interface Design Programme in 2017. Each team has to redesign a website. Create expressive, inventive visual experiences on the browser. Create with contemporary web technologies. Avoid usability, readability, and flexibility concerns. Act. Ignore Erwartungskonformität.
The class outcome pleased me. This overview page shows all results. Four diverse projects address the challenge.
1. ZKM by Frederic Haase and Jonas Köpfer
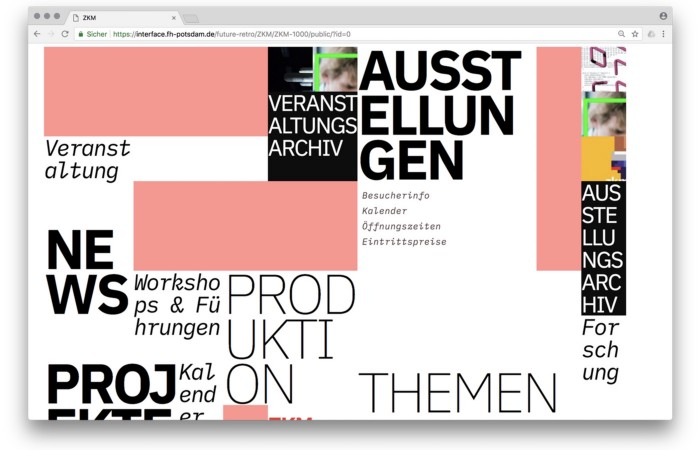
Frederic and Jonas began their experiments on the ZKM website. The ZKM is Germany's leading media art exhibition location, but its website remains conventional. It's useful but not avant-garde like the shows' art.
Frederic and Jonas designed the ZKM site's concept, aesthetic language, and technical configuration to reflect the museum's progressive approach. A generative design engine generates new layouts for each page load.
ZKM redesign.
2. Streem by Daria Thies, Bela Kurek, and Lucas Vogel

Street art magazine Streem. It promotes new artists and societal topics. Streem includes artwork, painting, photography, design, writing, and journalism. Daria, Bela, and Lucas used these influences to develop a conceptual metropolis. They designed four neighborhoods to reflect magazine sections for their prototype. For a legible city, they use powerful illustrative styles and spatial typography.
Streem makeover.
3. Medium by Amelie Kirchmeyer and Fabian Schultz
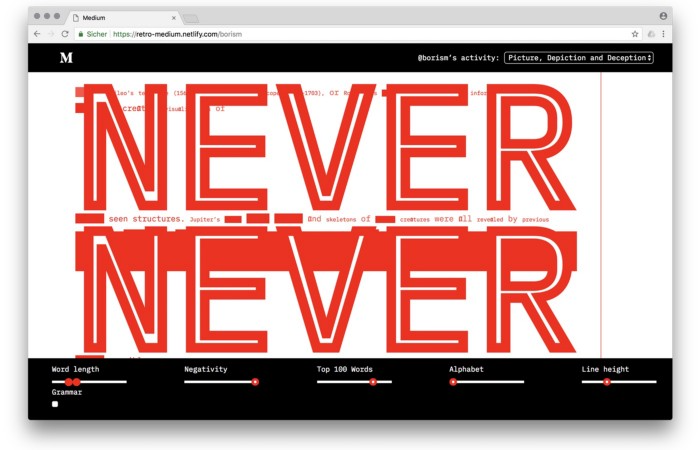
Amelie and Fabian structured. Instead of developing a form for a tale, they dissolved a web page into semantic, syntactical, and statistical aspects. HTML's flexibility was their goal. They broke Medium posts into experimental typographic space.
Medium revamp.
4. Hacker News by Fabian Dinklage and Florian Zia
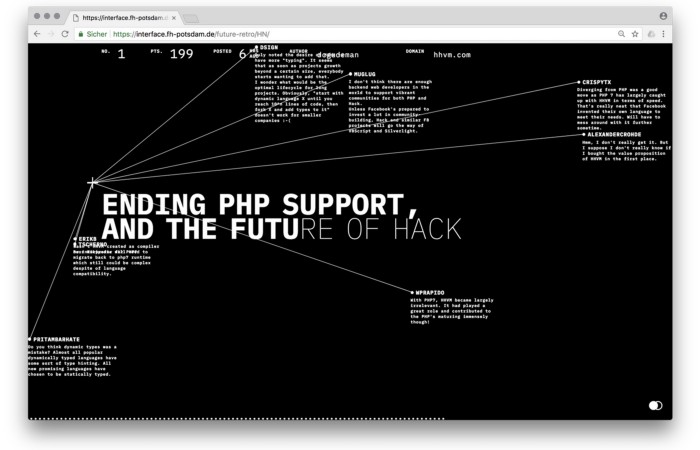
Florian and Fabian made Hacker News interactive. The social networking site aggregates computer science and IT news. Its voting and debate features are extensive despite its simple style. Fabian and Florian transformed the structure into a typographic timeline and network area. News and comments sequence and connect the visuals. To read Hacker News, they connected their design to the API. Hacker News makeover.
Communication is not legibility, said Carson. Apply this to web design today. Modern websites must be legible, usable, responsive, and accessible. They shouldn't limit its visual palette. Visual and human-centered design are not stereotypes.
I want radical, generative, evocative, insightful, adequate, content-specific, and intelligent site design. I want to rediscover web design experimentation. More surprises please. I hope the web will appear different in 23 years.
Update: this essay has sparked a lively discussion! I wrote a brief response to the debate's most common points: Creativity vs. Usability

Al Anany
3 years ago
Notion AI Might Destroy Grammarly and Jasper
The trick Notion could use is simply Facebook-ing the hell out of them.

*Time travel to fifteen years ago.* Future-Me: “Hey! What are you up to?” Old-Me: “I am proofreading an article. It’s taking a few hours, but I will be done soon.” Future-Me: “You know, in the future, you will be using a google chrome plugin called Grammarly that will help you easily proofread articles in half that time.” Old-Me: “What is… Google Chrome?” Future-Me: “Gosh…”
I love Grammarly. It’s one of those products that I personally feel the effects of. I mean, Space X is a great company. But I am not a rocket writing this article in space (or am I?)…
No, I’m not. So I don’t personally feel a connection to Space X. So, if a company collapse occurs in the morning, I might write about it. But I will have zero emotions regarding it.
Yet, if Grammarly fails tomorrow, I will feel 1% emotionally distressed. So looking at the title of this article, you’d realize that I am betting against them. This is how much I believe in the critical business model that’s taking over the world, the one of Notion.
Notion How frequently do you go through your notes?
Grammarly is everywhere, which helps its success. Grammarly is available when you update LinkedIn on Chrome. Grammarly prevents errors in Google Docs.
My internal concentration isn't apparent in the previous paragraph. Not Grammarly. I should have used Chrome to make a Google doc and LinkedIn update. Without this base, Grammarly will be useless.
So, welcome to this business essay.
Grammarly provides a solution.
Another issue is resolved by Jasper.
Your entire existence is supposed to be contained within Notion.
New Google Chrome is offline. It's an all-purpose notepad (in the near future.)
How should I start my blog? Enter it in Note.
an update on LinkedIn? If you mention it, it might be automatically uploaded there (with little help from another app.)
An advanced thesis? You can brainstorm it with your coworkers.
This ad sounds great! I won't cry if Notion dies tomorrow.
I'll reread the following passages to illustrate why I think Notion could kill Grammarly and Jasper.
Notion is a fantastic app that incubates your work.
Smartly, they began with note-taking.
Hopefully, your work will be on Notion. Grammarly and Jasper are still must-haves.
Grammarly will proofread your typing while Jasper helps with copywriting and AI picture development.
They're the best, therefore you'll need them. Correct? Nah.
Notion might bombard them with Facebook posts.
Notion: “Hi Grammarly, do you want to sell your product to us?” Grammarly: “Dude, we are more valuable than you are. We’ve even raised $400m, while you raised $342m. Our last valuation round put us at $13 billion, while yours put you at $10 billion. Go to hell.” Notion: “Okay, we’ll speak again in five years.”
Notion: “Jasper, wanna sell?” Jasper: “Nah, we’re deep into AI and the field. You can’t compete with our people.” Notion: “How about you either sell or you turn into a Snapchat case?” Jasper: “…”
Notion is your home. Grammarly is your neighbor. Your track is Jasper.
What if you grew enough vegetables in your backyard to avoid the supermarket? No more visits.
What if your home had a beautiful treadmill? You won't rush outside as much (I disagree with my own metaphor). (You get it.)
It's Facebooking. Instagram Stories reduced your Snapchat usage. Notion will reduce your need to use Grammarly.
The Final Piece of the AI Puzzle
Let's talk about Notion first, since you've probably read about it everywhere.
They raised $343 million, as I previously reported, and bought four businesses
According to Forbes, Notion will have more than 20 million users by 2022. The number of users is up from 4 million in 2020.
If raising $1.8 billion was impressive, FTX wouldn't have fallen.
This article compares the basic product to two others. Notion is a day-long app.
Notion has released Notion AI to support writers. It's early, so it's not as good as Jasper. Then-Jasper isn't now-Jasper. In five years, Notion AI will be different.
With hard work, they may construct a Jasper-like writing assistant. They have resources and users.
At this point, it's all speculation. Jasper's copywriting is top-notch. Grammarly's proofreading is top-notch. Businesses are constrained by user activities.
If Notion's future business movements are strategic, they might become a blue ocean shark (or get acquired by an unbelievable amount.)
I love business mental teasers, so tell me:
How do you feel? Are you a frequent Notion user?
Do you dispute my position? I enjoy hearing opposing viewpoints.
Ironically, I proofread this with Grammarly.
