More on Web3 & Crypto

CyberPunkMetalHead
3 years ago
It's all about the ego with Terra 2.0.
UST depegs and LUNA crashes 99.999% in a fraction of the time it takes the Moon to orbit the Earth.
Fat Man, a Terra whistle-blower, promises to expose Do Kwon's dirty secrets and shady deals.

The Terra community has voted to relaunch Terra LUNA on a new blockchain. The Terra 2.0 Pheonix-1 blockchain went live on May 28, 2022, and people were airdropped the new LUNA, now called LUNA, while the old LUNA became LUNA Classic.
Does LUNA deserve another chance? To answer this, or at least start a conversation about the Terra 2.0 chain's advantages and limitations, we must assess its fundamentals, ideology, and long-term vision.
Whatever the result, our analysis must be thorough and ruthless. A failure of this magnitude cannot happen again, so we must magnify every potential breaking point by 10.
Will UST and LUNA holders be compensated in full?
The obvious. First, and arguably most important, is to restore previous UST and LUNA holders' bags.
Terra 2.0 has 1,000,000,000,000 tokens to distribute.
25% of a community pool
Holders of pre-attack LUNA: 35%
10% of aUST holders prior to attack
Holders of LUNA after an attack: 10%
UST holders as of the attack: 20%
Every LUNA and UST holder has been compensated according to the above proposal.
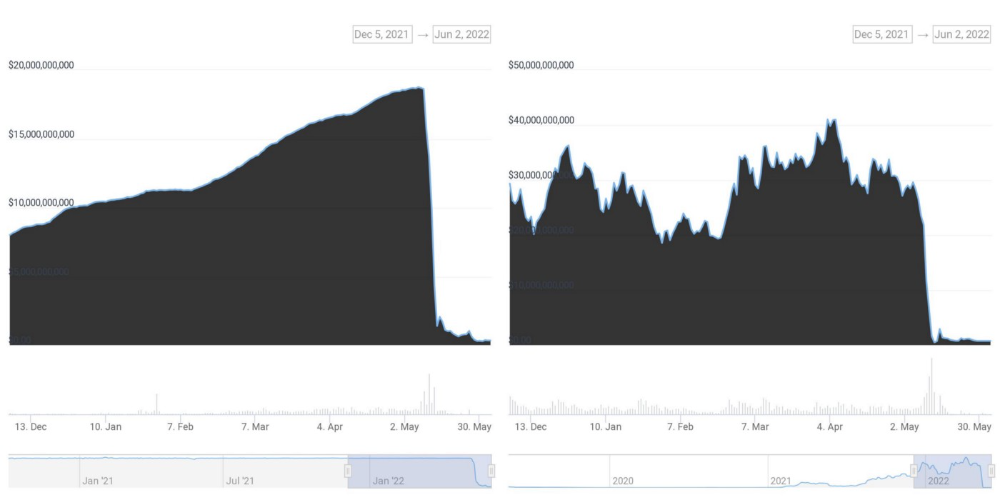
According to self-reported data, the new chain has 210.000.000 tokens and a $1.3bn marketcap. LUNC and UST alone lost $40bn. The new token must fill this gap. Since launch:
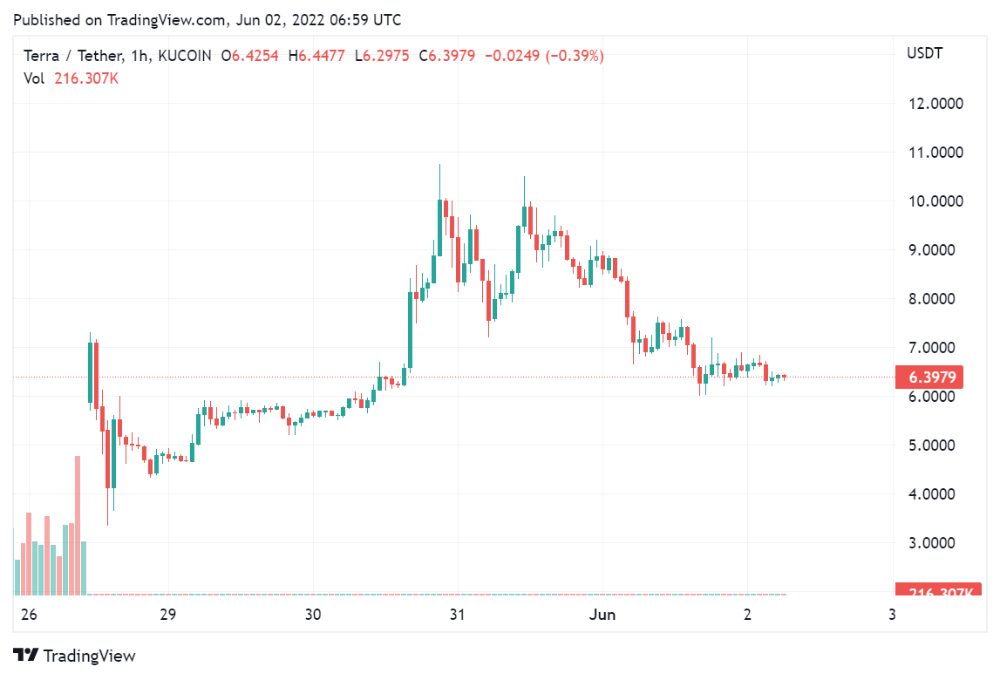
LUNA holders collectively own $1b worth of LUNA if we subtract the 25% community pool airdrop from the current market cap and assume airdropped LUNA was never sold.
At the current supply, the chain must grow 40 times to compensate holders. At the current supply, LUNA must reach $240.
LUNA needs a full-on Bull Market to make LUNC and UST holders whole.
Who knows if you'll be whole? From the time you bought to the amount and price, there are too many variables to determine if Terra can cover individual losses.
The above distribution doesn't consider individual cases. Terra didn't solve individual cases. It would have been huge.
What does LUNA offer in terms of value?
UST's marketcap peaked at $18bn, while LUNC's was $41bn. LUNC and UST drove the Terra chain's value.
After it was confirmed (again) that algorithmic stablecoins are bad, Terra 2.0 will no longer support them.
Algorithmic stablecoins contributed greatly to Terra's growth and value proposition. Terra 2.0 has no product without algorithmic stablecoins.
Terra 2.0 has an identity crisis because it has no actual product. It's like Volkswagen faking carbon emission results and then stopping car production.
A project that has already lost the trust of its users and nearly all of its value cannot survive without a clear and in-demand use case.
Do Kwon, how about him?
Oh, the Twitter-caller-poor? Who challenges crypto billionaires to break his LUNA chain? Who dissolved Terra Labs South Korea before depeg? Arrogant guy?
That's not a good image for LUNA, especially when making amends. I think he should step down and let a nicer person be Terra 2.0's frontman.
The verdict
Terra has a terrific community with an arrogant, unlikeable leader. The new LUNA chain must grow 40 times before it can start making up its losses, and even then, not everyone's losses will be covered.
I won't invest in Terra 2.0 or other algorithmic stablecoins in the near future. I won't be near any Do Kwon-related project within 100 miles. My opinion.
Can Terra 2.0 be saved? Comment below.
Sam Hickmann
4 years ago
A quick guide to formatting your text on INTΞGRITY
[06/20/2022 update] We have now implemented a powerful text editor, but you can still use markdown.
Markdown:
Headers
SYNTAX:
# This is a heading 1
## This is a heading 2
### This is a heading 3
#### This is a heading 4
RESULT:
This is a heading 1
This is a heading 2
This is a heading 3
This is a heading 4
Emphasis
SYNTAX:
**This text will be bold**
~~Strikethrough~~
*You **can** combine them*
RESULT:
This text will be italic
This text will be bold
You can combine them
Images
SYNTAX:

RESULT:
Videos
SYNTAX:
https://www.youtube.com/watch?v=7KXGZAEWzn0
RESULT:
Links
SYNTAX:
[Int3grity website](https://www.int3grity.com)
RESULT:
Tweets
SYNTAX:
https://twitter.com/samhickmann/status/1503800505864130561
RESULT:
Blockquotes
SYNTAX:
> Human beings face ever more complex and urgent problems, and their effectiveness in dealing with these problems is a matter that is critical to the stability and continued progress of society. \- Doug Engelbart, 1961
RESULT:
Human beings face ever more complex and urgent problems, and their effectiveness in dealing with these problems is a matter that is critical to the stability and continued progress of society. - Doug Engelbart, 1961
Inline code
SYNTAX:
Text inside `backticks` on a line will be formatted like code.
RESULT:
Text inside backticks on a line will be formatted like code.
Code blocks
SYNTAX:
'''js
function fancyAlert(arg) {
if(arg) {
$.facebox({div:'#foo'})
}
}
'''
RESULT:
function fancyAlert(arg) {
if(arg) {
$.facebox({div:'#foo'})
}
}
Maths
We support LaTex to typeset math. We recommend reading the full documentation on the official website
SYNTAX:
$$[x^n+y^n=z^n]$$
RESULT:
[x^n+y^n=z^n]
Tables
SYNTAX:
| header a | header b |
| ---- | ---- |
| row 1 col 1 | row 1 col 2 |
RESULT:
| header a | header b | header c |
|---|---|---|
| row 1 col 1 | row 1 col 2 | row 1 col 3 |

Sam Bourgi
3 years ago
DAOs are legal entities in Marshall Islands.
The Pacific island state recognizes decentralized autonomous organizations.
The Republic of the Marshall Islands has recognized decentralized autonomous organizations (DAOs) as legal entities, giving collectively owned and managed blockchain projects global recognition.
The Marshall Islands' amended the Non-Profit Entities Act 2021 that now recognizes DAOs, which are blockchain-based entities governed by self-organizing communities. Incorporating Admiralty LLC, the island country's first DAO, was made possible thanks to the amendement. MIDAO Directory Services Inc., a domestic organization established to assist DAOs in the Marshall Islands, assisted in the incorporation.
The new law currently allows any DAO to register and operate in the Marshall Islands.
“This is a unique moment to lead,” said Bobby Muller, former Marshall Islands chief secretary and co-founder of MIDAO. He believes DAOs will help create “more efficient and less hierarchical” organizations.
A global hub for DAOs, the Marshall Islands hopes to become a global hub for DAO registration, domicile, use cases, and mass adoption. He added:
"This includes low-cost incorporation, a supportive government with internationally recognized courts, and a technologically open environment."
According to the World Bank, the Marshall Islands is an independent island state in the Pacific Ocean near the Equator. To create a blockchain-based cryptocurrency that would be legal tender alongside the US dollar, the island state has been actively exploring use cases for digital assets since at least 2018.
In February 2018, the Marshall Islands approved the creation of a new cryptocurrency, Sovereign (SOV). As expected, the IMF has criticized the plan, citing concerns that a digital sovereign currency would jeopardize the state's financial stability. They have also criticized El Salvador, the first country to recognize Bitcoin (BTC) as legal tender.
Marshall Islands senator David Paul said the DAO legislation does not pose the same issues as a government-backed cryptocurrency. “A sovereign digital currency is financial and raises concerns about money laundering,” . This is more about giving DAOs legal recognition to make their case to regulators, investors, and consumers.
You might also like

Mickey Mellen
2 years ago
Shifting from Obsidian to Tana?

I relocated my notes database from Roam Research to Obsidian earlier this year expecting to stay there for a long. Obsidian is a terrific tool, and I explained my move in that post.
Moving everything to Tana faster than intended. Tana? Why?
Tana is just another note-taking app, but it does it differently. Three note-taking apps existed before Tana:
simple note-taking programs like Apple Notes and Google Keep.
Roam Research and Obsidian are two graph-style applications that assisted connect your notes.
You can create effective tables and charts with data-focused tools like Notion and Airtable.
Tana is the first great software I've encountered that combines graph and data notes. Google Keep will certainly remain my rapid notes app of preference. This Shu Omi video gives a good overview:
Tana handles everything I did in Obsidian with books, people, and blog entries, plus more. I can find book quotes, log my workouts, and connect my thoughts more easily. It should make writing blog entries notes easier, so we'll see.
Tana is now invite-only, but if you're interested, visit their site and sign up. As Shu noted in the video above, the product hasn't been published yet but seems quite polished.
Whether I stay with Tana or not, I'm excited to see where these apps are going and how they can benefit us all.

Aaron Dinin, PhD
3 years ago
I put my faith in a billionaire, and he destroyed my business.
How did his money blind me?

Like most fledgling entrepreneurs, I wanted a mentor. I met as many nearby folks with "entrepreneur" in their LinkedIn biographies for coffee.
These meetings taught me a lot, and I'd suggest them to any new creator. Attention! Meeting with many experienced entrepreneurs means getting contradictory advice. One entrepreneur will tell you to do X, then the next one you talk to may tell you to do Y, which are sometimes opposites. You'll have to chose which suggestion to take after the chats.
I experienced this. Same afternoon, I had two coffee meetings with experienced entrepreneurs. The first meeting was with a billionaire entrepreneur who took his company public.
I met him in a swanky hotel lobby and ordered a drink I didn't pay for. As a fledgling entrepreneur, money was scarce.
During the meeting, I demoed the software I'd built, he liked it, and we spent the hour discussing what features would make it a success. By the end of the meeting, he requested I include a killer feature we both agreed would attract buyers. The feature was complex and would require some time. The billionaire I was sipping coffee with in a beautiful hotel lobby insisted people would love it, and that got me enthusiastic.
The second meeting was with a young entrepreneur who had recently raised a small amount of investment and looked as eager to pitch me as I was to pitch him. I forgot his name. I mostly recall meeting him in a filthy coffee shop in a bad section of town and buying his pricey cappuccino. Water for me.
After his pitch, I demoed my app. When I was done, he barely noticed. He questioned my customer acquisition plan. Who was my client? What did they offer? What was my plan? Etc. No decent answers.
After our meeting, he insisted I spend more time learning my market and selling. He ignored my questions about features. Don't worry about features, he said. Customers will request features. First, find them.
Putting your faith in results over relevance
Problems plagued my afternoon. I met with two entrepreneurs who gave me differing advice about how to proceed, and I had to decide which to pursue. I couldn't decide.
Ultimately, I followed the advice of the billionaire.
Obviously.
Who wouldn’t? That was the guy who clearly knew more.
A few months later, I constructed the feature the billionaire said people would line up for.
The new feature was unpopular. I couldn't even get the billionaire to answer an email showing him what I'd done. He disappeared.
Within a few months, I shut down the company, wasting all the time and effort I'd invested into constructing the killer feature the billionaire said I required.
Would follow the struggling entrepreneur's advice have saved my company? It would have saved me time in retrospect. Potential consumers would have told me they didn't want what I was producing, and I could have shut down the company sooner or built something they did want. Both outcomes would have been better.
Now I know, but not then. I favored achievement above relevance.
Success vs. relevance
The millionaire gave me advice on building a large, successful public firm. A successful public firm is different from a startup. Priorities change in the last phase of business building, which few entrepreneurs reach. He gave wonderful advice to founders trying to double their stock values in two years, but it wasn't beneficial for me.
The other failing entrepreneur had relevant, recent experience. He'd recently been in my shoes. We still had lots of problems. He may not have achieved huge success, but he had valuable advice on how to pass the closest hurdle.
The money blinded me at the moment. Not alone So much of company success is defined by money valuations, fundraising, exits, etc., so entrepreneurs easily fall into this trap. Money chatter obscures the value of knowledge.
Don't base startup advice on a person's income. Focus on what and when the person has learned. Relevance to you and your goals is more important than a person's accomplishments when considering advice.
Jack Burns
3 years ago
Here's what to expect from NASA Artemis 1 and why it's significant.
NASA's Artemis 1 mission will help return people to the Moon after a half-century break. The mission is a shakedown cruise for NASA's Space Launch System and Orion Crew Capsule.
The spaceship will visit the Moon, deploy satellites, and enter orbit. NASA wants to practice operating the spacecraft, test the conditions people will face on the Moon, and ensure a safe return to Earth.
We asked Jack Burns, a space scientist at the University of Colorado Boulder and former member of NASA's Presidential Transition Team, to describe the mission, explain what the Artemis program promises for space exploration, and reflect on how the space program has changed in the half-century since humans last set foot on the moon.
What distinguishes Artemis 1 from other rockets?
Artemis 1 is the Space Launch System's first launch. NASA calls this a "heavy-lift" vehicle. It will be more powerful than Apollo's Saturn V, which transported people to the Moon in the 1960s and 1970s.
It's a new sort of rocket system with two strap-on solid rocket boosters from the space shuttle. It's a mix of the shuttle and Saturn V.
The Orion Crew Capsule will be tested extensively. It'll spend a month in the high-radiation Moon environment. It will also test the heat shield, which protects the capsule and its occupants at 25,000 mph. The heat shield must work well because this is the fastest capsule descent since Apollo.
This mission will also carry miniature Moon-orbiting satellites. These will undertake vital precursor science, including as examining further into permanently shadowed craters where scientists suspect there is water and measuring the radiation environment to see long-term human consequences.
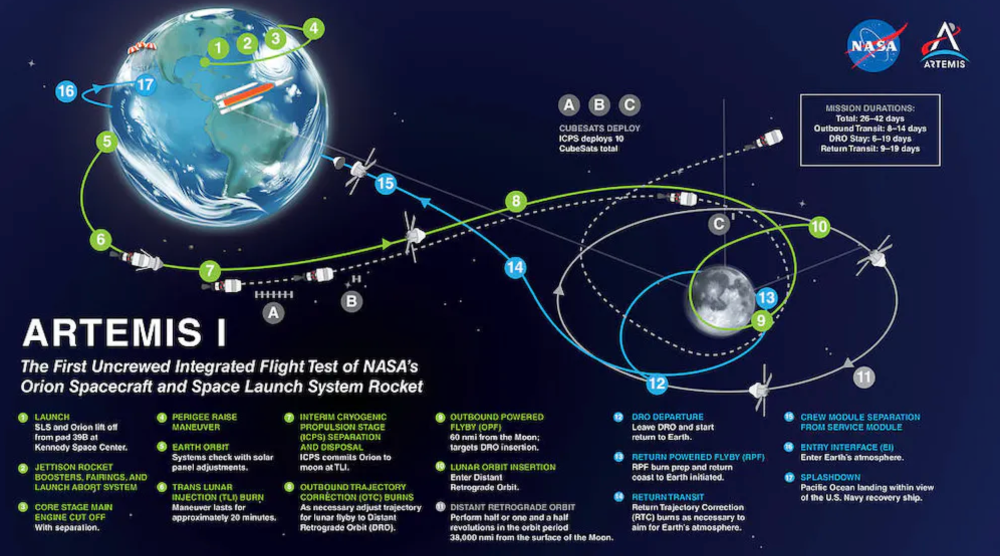
Artemis 1 will launch, fly to the Moon, place satellites, orbit it, return to Earth, and splash down in the ocean. NASA.
What's Artemis's goal? What launches are next?
The mission is a first step toward Artemis 3, which will lead to the first human Moon missions since 1972. Artemis 1 is unmanned.
Artemis 2 will have astronauts a few years later. Like Apollo 8, it will be an orbital mission that circles the Moon and returns. The astronauts will orbit the Moon longer and test everything with a crew.
Eventually, Artemis 3 will meet with the SpaceX Starship on the Moon's surface and transfer people. Orion will stay in orbit while the lunar Starship lands astronauts. They'll go to the Moon's south pole to investigate the water ice there.
Artemis is reminiscent of Apollo. What's changed in 50 years?
Kennedy wanted to beat the Soviets to the Moon with Apollo. The administration didn't care much about space flight or the Moon, but the goal would place America first in space and technology.
You live and die by the sword if you do that. When the U.S. reached the Moon, it was over. Russia lost. We planted flags and did science experiments. Richard Nixon canceled the program after Apollo 11 because the political goals were attained.
Large rocket with two boosters between two gates

NASA's new Space Launch System is brought to a launchpad. NASA
50 years later... It's quite different. We're not trying to beat the Russians, Chinese, or anyone else, but to begin sustainable space exploration.
Artemis has many goals. It includes harnessing in-situ resources like water ice and lunar soil to make food, fuel, and building materials.
SpaceX is part of this first journey to the Moon's surface, therefore the initiative is also helping to develop a lunar and space economy. NASA doesn't own the Starship but is buying seats for astronauts. SpaceX will employ Starship to transport cargo, private astronauts, and foreign astronauts.
Fifty years of technology advancement has made getting to the Moon cheaper and more practical, and computer technology allows for more advanced tests. 50 years of technological progress have changed everything. Anyone with enough money can send a spacecraft to the Moon, but not humans.
Commercial Lunar Payload Services engages commercial companies to develop uncrewed Moon landers. We're sending a radio telescope to the Moon in January. Even 10 years ago, that was impossible.
Since humans last visited the Moon 50 years ago, technology has improved greatly.
What other changes does Artemis have in store?
The government says Artemis 3 will have at least one woman and likely a person of color.
I'm looking forward to seeing more diversity so young kids can say, "Hey, there's an astronaut that looks like me. I can do this. I can be part of the space program.”
