StableGains lost $42M in Anchor Protocol.
StableGains lost millions of dollars in customer funds in Anchor Protocol without telling its users. The Anchor Protocol offered depositors 19-20% APY before its parent ecosystem, Terra LUNA, lost tens of billions of dollars in market capitalization as LUNA fell below $0.01 and its stablecoin (UST) collapsed.
A Terra Research Forum member raised the alarm. StableGains changed its homepage and Terms and Conditions to reflect how it mitigates risk, a tacit admission that it should have done so from the start.
StableGains raised $600,000 in YCombinator's W22 batch. Moonfire, Broom Ventures, and Goodwater Capital invested $3 million more.
StableGains' 15% yield product attracted $42 million in deposits. StableGains kept most of its deposits in Anchor's UST pool earning 19-20% APY, kept one-quarter of the interest as a management fee, and then gave customers their promised 15% APY. It lost almost all customer funds when UST melted down. It changed withdrawal times, hurting customers.
- StableGains said de-pegging was unlikely. According to its website, 1 UST can be bought and sold for $1 of LUNA. LUNA became worthless, and Terra shut down its blockchain.
- It promised to diversify assets across several stablecoins to reduce the risk of one losing its $1 peg, but instead kept almost all of them in one basket.
- StableGains promised withdrawals in three business days, even if a stablecoin needed time to regain its peg. StableGains uses Coinbase for deposits and withdrawals, and customers receive the exact amount of USDC requested.
StableGains scrubs its website squeaky clean
StableGains later edited its website to say it only uses the "most trusted and tested stablecoins" and extended withdrawal times from three days to indefinite time "in extreme cases."
Previously, USDC, TerraUST (UST), and Dai were used (DAI). StableGains changed UST-related website content after the meltdown. It also removed most references to DAI.
Customers noticed a new clause in the Terms and Conditions denying StableGains liability for withdrawal losses. This new clause would have required customers to agree not to sue before withdrawing funds, avoiding a class-action lawsuit.
Customers must sign a waiver to receive a refund.
Erickson Kramer & Osborne law firm has asked StableGains to preserve all internal documents on customer accounts, marketing, and TerraUSD communications. The firm has not yet filed a lawsuit.
Thousands of StableGains customers lost an estimated $42 million.
Celsius Network customers also affected
CEL used Terra LUNA's Anchor Protocol. Celsius users lost money in the crypto market crash and UST meltdown. Many held CEL and LUNA as yielding deposits.
CEO Alex Mashinsky accused "unknown malefactors" of targeting Celsius Network without evidence. Celsius has not publicly investigated this claim as of this article's publication.
CEL fell before UST de-pegged. On June 2, 2021, it reached $8.01. May 19's close: $0.82.
When some Celsius Network users threatened to leave over token losses, Mashinsky replied, "Leave if you don't think I'm sincere and working harder than you, seven days a week."
Celsius Network withdrew $500 million from Anchor Protocol, but smaller holders had trouble.
Read original article here
More on Web3 & Crypto

Caleb Naysmith
3 years ago Draft
A Myth: Decentralization
It’s simply not conceivable, or at least not credible.

One of the most touted selling points of Crypto has always been this grandiose idea of decentralization. Bitcoin first arose in 2009 after the housing crisis and subsequent crash that came with it. It aimed to solve this supposed issue of centralization. Nobody “owns” Bitcoin in theory, so the idea then goes that it won’t be subject to the same downfalls that led to the 2008 crash or similarly speculative events that led to the 2008 disaster. The issue is the banks, not the human nature associated with the greedy individuals running them.
Subsequent blockchains have attempted to fix many of the issues of Bitcoin by increasing capacity, decreasing the costs and processing times associated with Bitcoin, and expanding what can be done with their blockchains. Since nobody owns Bitcoin, it hasn’t really been able to be expanded on. You have people like Vitalk Buterin, however, that actively work on Ethereum though.
The leap from Bitcoin to Ethereum was a massive leap toward centralization, and the trend has only gotten worse. In fact, crypto has since become almost exclusively centralized in recent years.
Decentralization is only good in theory
It’s a good idea. In fact, it’s a wonderful idea. However, like other utopian societies, individuals misjudge human nature and greed. In a perfect world, decentralization would certainly be a wonderful idea because sure, people may function as their own banks, move payments immediately, remain anonymous, and so on. However, underneath this are a couple issues:
You can already send money instantaneously today.
They are not decentralized.
Decentralization is a bad idea.
Being your own bank is a stupid move.
Let’s break these down. Some are quite simple, but lets have a look.
Sending money right away
One thing with crypto is the idea that you can send payments instantly. This has pretty much been entirely solved in current times. You can transmit significant sums of money instantly for a nominal cost and it’s instantaneously cleared. Venmo was launched in 2009 and has since increased to prominence, and currently is on most people's phones. I can directly send ANY amount of money quickly from my bank to another person's Venmo account.
Comparing that with ETH and Bitcoin, Venmo wins all around. I can send money to someone for free instantly in dollars and the only fee paid is optional depending on when you want it.
Both Bitcoin and Ethereum are subject to demand. If the blockchains have a lot of people trying to process transactions fee’s go up, and the time that it takes to receive your crypto takes longer. When Ethereum gets bad, people have reported spending several thousand of dollars on just 1 transaction.
These transactions take place via “miners” bundling and confirming transactions, then recording them on the blockchain to confirm that the transaction did indeed happen. They charge fees to do this and are also paid in Bitcoin/ETH. When a transaction is confirmed, it's then sent to the other users wallet. This within itself is subject to lots of controversy because each transaction needs to be confirmed 6 times, this takes massive amounts of power, and most of the power is wasted because this is an adversarial system in which the person that mines the transaction gets paid, and everyone else is out of luck. Also, these could theoretically be subject to a “51% attack” in which anyone with over 51% of the mining hash rate could effectively control all of the transactions, and reverse transactions while keeping the BTC resulting in “double spending”.
There are tons of other issues with this, but essentially it means: They rely on these third parties to confirm the transactions. Without people confirming these transactions, Bitcoin stalls completely, and if anyone becomes too dominant they can effectively control bitcoin.
Not to mention, these transactions are in Bitcoin and ETH, not dollars. So, you need to convert them to dollars still, and that's several more transactions, and likely to take several days anyway as the centralized exchange needs to send you the money by traditional methods.
They are not distributed
That takes me to the following point. This isn’t decentralized, at all. Bitcoin is the closest it gets because Satoshi basically closed it to new upgrades, although its still subject to:
Whales
Miners
It’s vital to realize that these are often the same folks. While whales aren’t centralized entities typically, they can considerably effect the price and outcome of Bitcoin. If the largest wallets holding as much as 1 million BTC were to sell, it’d effectively collapse the price perhaps beyond repair. However, Bitcoin can and is pretty much controlled by the miners. Further, Bitcoin is more like an oligarchy than decentralized. It’s been effectively used to make the rich richer, and both the mining and price is impacted by the rich. The overwhelming minority of those actually using it are retail investors. The retail investors are basically never the ones generating money from it either.
As far as ETH and other cryptos go, there is realistically 0 case for them being decentralized. Vitalik could not only kill it but even walking away from it would likely lead to a significant decline. It has tons of issues right now that Vitalik has promised to fix with the eventual Ethereum 2.0., and stepping away from it wouldn’t help.
Most tokens as well are generally tied to some promise of future developments and creators. The same is true for most NFT projects. The reason 99% of crypto and NFT projects fail is because they failed to deliver on various promises or bad dev teams, or poor innovation, or the founders just straight up stole from everyone. I could go more in-depth than this but go find any project and if there is a dev team, company, or person tied to it then it's likely, not decentralized. The success of that project is directly tied to the dev team, and if they wanted to, most hold large wallets and could sell it all off effectively killing the project. Not to mention, any crypto project that doesn’t have a locked contract can 100% be completely rugged and they can run off with all of the money.
Decentralization is undesirable
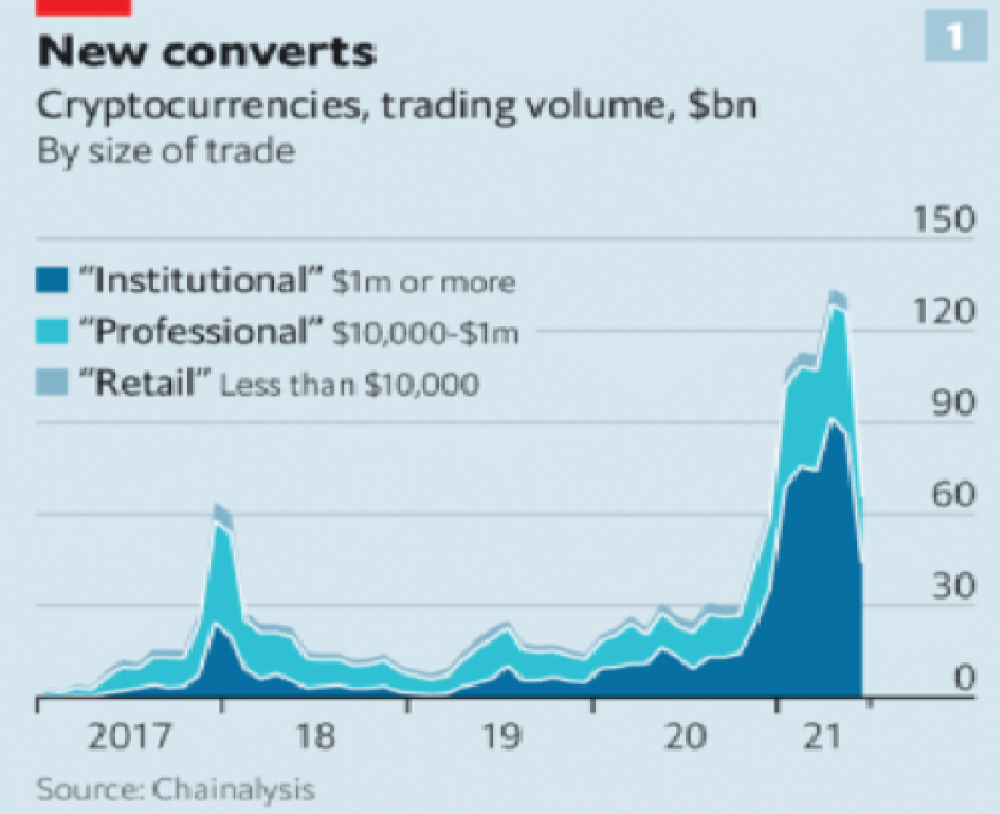
Even if they were decentralized then it would not be a good thing. The graphic above indicates this is effectively a rich person’s unregulated playground… so it’s exactly like… the very issue it tried to solve?
Not to mention, it’s supposedly meant to prevent things like 2008, but is regularly subjected to 50–90% drawdowns in value? Back when Bitcoin was only known in niche parts of the dark web and illegal markets, it would regularly drop as much as 90% and has a long history of massive drawdowns.
The majority of crypto is blatant scams, and ALL of crypto is a “zero” or “negative” sum game in that it relies on the next person buying for people to make money. This is not a good thing. This has yet to solve any issues around what caused the 2008 crisis. Rather, it seemingly amplified all of the bad parts of it actually. Crypto is the ultimate speculative asset and realistically has no valuation metric. People invest in Apple because it has revenue and cash on hand. People invest in crypto purely for speculation. The lack of regulation or accountability means this is amplified to the most extreme degree where anything goes: Fraud, deception, pump and dumps, scams, etc. This results in a pure speculative madhouse where, unsurprisingly, only the rich win. Not only that but the deck is massively stacked in against the everyday investor because you can’t do a pump and dump without money.
At the heart of all of this is still the same issues: greed and human nature. However, in setting out to solve the issues that allowed 2008 to happen, they made something that literally took all of the bad parts of 2008 and then amplified it. 2008, similarly, was due to greed and human nature but was allowed to happen due to lack of oversite, rich people's excessive leverage over the poor, and excessive speculation. Crypto trades SOLELY on human emotion, has 0 oversite, is pure speculation, and the power dynamic is just as bad or worse.
Why should each individual be their own bank?
This is the last one, and it's short and basic. Why do we want people functioning as their own bank? Everything we do relies on another person. Without the internet, and internet providers there is no crypto. We don’t have people functioning as their own home and car manufacturers or internet service providers. Sure, you might specialize in some of these things, but masquerading as your own bank is a horrible idea.
I am not in the banking industry so I don’t know all the issues with banking. Most people aren’t in banking or crypto, so they don’t know the ENDLESS scams associated with it, and they are bound to lose their money eventually.
If you appreciate this article and want to read more from me and authors like me, without any limits, consider buying me a coffee: buymeacoffee.com/calebnaysmith
:max_bytes(150000):strip_icc():gifv():format(webp)/reiff_headshot-5bfc2a60c9e77c00519a70bd.jpg)
Nathan Reiff
3 years ago
Howey Test and Cryptocurrencies: 'Every ICO Is a Security'
What Is the Howey Test?
To determine whether a transaction qualifies as a "investment contract" and thus qualifies as a security, the Howey Test refers to the U.S. Supreme Court cass: the Securities Act of 1933 and the Securities Exchange Act of 1934. According to the Howey Test, an investment contract exists when "money is invested in a common enterprise with a reasonable expectation of profits from others' efforts."
The test applies to any contract, scheme, or transaction. The Howey Test helps investors and project backers understand blockchain and digital currency projects. ICOs and certain cryptocurrencies may be found to be "investment contracts" under the test.
Understanding the Howey Test
The Howey Test comes from the 1946 Supreme Court case SEC v. W.J. Howey Co. The Howey Company sold citrus groves to Florida buyers who leased them back to Howey. The company would maintain the groves and sell the fruit for the owners. Both parties benefited. Most buyers had no farming experience and were not required to farm the land.
The SEC intervened because Howey failed to register the transactions. The court ruled that the leaseback agreements were investment contracts.
This established four criteria for determining an investment contract. Investing contract:
- An investment of money
- n a common enterprise
- With the expectation of profit
- To be derived from the efforts of others
In the case of Howey, the buyers saw the transactions as valuable because others provided the labor and expertise. An income stream was obtained by only investing capital. As a result of the Howey Test, the transaction had to be registered with the SEC.
Howey Test and Cryptocurrencies
Bitcoin is notoriously difficult to categorize. Decentralized, they evade regulation in many ways. Regardless, the SEC is looking into digital assets and determining when their sale qualifies as an investment contract.
The SEC claims that selling digital assets meets the "investment of money" test because fiat money or other digital assets are being exchanged. Like the "common enterprise" test.
Whether a digital asset qualifies as an investment contract depends on whether there is a "expectation of profit from others' efforts."
For example, buyers of digital assets may be relying on others' efforts if they expect the project's backers to build and maintain the digital network, rather than a dispersed community of unaffiliated users. Also, if the project's backers create scarcity by burning tokens, the test is met. Another way the "efforts of others" test is met is if the project's backers continue to act in a managerial role.
These are just a few examples given by the SEC. If a project's success is dependent on ongoing support from backers, the buyer of the digital asset is likely relying on "others' efforts."
Special Considerations
If the SEC determines a cryptocurrency token is a security, many issues arise. It means the SEC can decide whether a token can be sold to US investors and forces the project to register.
In 2017, the SEC ruled that selling DAO tokens for Ether violated federal securities laws. Instead of enforcing securities laws, the SEC issued a warning to the cryptocurrency industry.
Due to the Howey Test, most ICOs today are likely inaccessible to US investors. After a year of ICOs, then-SEC Chair Jay Clayton declared them all securities.
SEC Chairman Gensler Agrees With Predecessor: 'Every ICO Is a Security'
Howey Test FAQs
How Do You Determine If Something Is a Security?
The Howey Test determines whether certain transactions are "investment contracts." Securities are transactions that qualify as "investment contracts" under the Securities Act of 1933 and the Securities Exchange Act of 1934.
The Howey Test looks for a "investment of money in a common enterprise with a reasonable expectation of profits from others' efforts." If so, the Securities Act of 1933 and the Securities Exchange Act of 1934 require disclosure and registration.
Why Is Bitcoin Not a Security?
Former SEC Chair Jay Clayton clarified in June 2018 that bitcoin is not a security: "Cryptocurrencies: Replace the dollar, euro, and yen with bitcoin. That type of currency is not a security," said Clayton.
Bitcoin, which has never sought public funding to develop its technology, fails the SEC's Howey Test. However, according to Clayton, ICO tokens are securities.
A Security Defined by the SEC
In the public and private markets, securities are fungible and tradeable financial instruments. The SEC regulates public securities sales.
The Supreme Court defined a security offering in SEC v. W.J. Howey Co. In its judgment, the court defines a security using four criteria:
- An investment contract's existence
- The formation of a common enterprise
- The issuer's profit promise
- Third-party promotion of the offering
Read original post.
James Howell
3 years ago
Which Metaverse Is Better, Decentraland or Sandbox?
The metaverse is the most commonly used term in current technology discussions. While the entire tech ecosystem awaits the metaverse's full arrival, defining it is difficult. Imagine the internet in the '80s! The metaverse is a three-dimensional virtual world where users can interact with digital solutions and each other as digital avatars.
The metaverse is a three-dimensional virtual world where users can interact with digital solutions and each other as digital avatars.
Among the metaverse hype, the Decentraland vs Sandbox debate has gained traction. Both are decentralized metaverse platforms with no central authority. So, what's the difference and which is better? Let us examine the distinctions between Decentraland and Sandbox.
2 Popular Metaverse Platforms Explained
The first step in comparing sandbox and Decentraland is to outline the definitions. Anyone keeping up with the metaverse news has heard of the two current leaders. Both have many similarities, but also many differences. Let us start with defining both platforms to see if there is a winner.
Decentraland
Decentraland, a fully immersive and engaging 3D metaverse, launched in 2017. It allows players to buy land while exploring the vast virtual universe. Decentraland offers a wide range of activities for its visitors, including games, casinos, galleries, and concerts. It is currently the longest-running metaverse project.
Decentraland began with a $24 million ICO and went public in 2020. The platform's virtual real estate parcels allow users to create a variety of experiences. MANA and LAND are two distinct tokens associated with Decentraland. MANA is the platform's native ERC-20 token, and users can burn MANA to get LAND, which is ERC-721 compliant. The MANA coin can be used to buy avatars, wearables, products, and names on Decentraland.
Sandbox
Sandbox, the next major player, began as a blockchain-based virtual world in 2011 and migrated to a 3D gaming platform in 2017. The virtual world allows users to create, play, own, and monetize their virtual experiences. Sandbox aims to empower artists, creators, and players in the blockchain community to customize the platform. Sandbox gives the ideal means for unleashing creativity in the development of the modern gaming ecosystem.
The project combines NFTs and DAOs to empower a growing community of gamers. A new play-to-earn model helps users grow as gamers and creators. The platform offers a utility token, SAND, which is required for all transactions.
What are the key points from both metaverse definitions to compare Decentraland vs sandbox?
It is ideal for individuals, businesses, and creators seeking new artistic, entertainment, and business opportunities. It is one of the rapidly growing Decentralized Autonomous Organization projects. Holders of MANA tokens also control the Decentraland domain.
Sandbox, on the other hand, is a blockchain-based virtual world that runs on the native token SAND. On the platform, users can create, sell, and buy digital assets and experiences, enabling blockchain-based gaming. Sandbox focuses on user-generated content and building an ecosystem of developers.
Sandbox vs. Decentraland
If you try to find what is better Sandbox or Decentraland, then you might struggle with only the basic definitions. Both are metaverse platforms offering immersive 3D experiences. Users can freely create, buy, sell, and trade digital assets. However, both have significant differences, especially in MANA vs SAND.
For starters, MANA has a market cap of $5,736,097,349 versus $4,528,715,461, giving Decentraland an advantage.
The MANA vs SAND pricing comparison is also noteworthy. A SAND is currently worth $3664, while a MANA is worth $2452.
The value of the native tokens and the market capitalization of the two metaverse platforms are not enough to make a choice. Let us compare Sandbox vs Decentraland based on the following factors.
Workstyle
The way Decentraland and Sandbox work is one of the main comparisons. From a distance, they both appear to work the same way. But there's a lot more to learn about both platforms' workings. Decentraland has 90,601 digital parcels of land.
Individual parcels of virtual real estate or estates with multiple parcels of land are assembled. It also has districts with similar themes and plazas, which are non-tradeable parcels owned by the community. It has three token types: MANA, LAND, and WEAR.
Sandbox has 166,464 plots of virtual land that can be grouped into estates. Estates are owned by one person, while districts are owned by two or more people. The Sandbox metaverse has four token types: SAND, GAMES, LAND, and ASSETS.
Age
The maturity of metaverse projects is also a factor in the debate. Decentraland is clearly the winner in terms of maturity. It was the first solution to create a 3D blockchain metaverse. Decentraland made the first working proof of concept public. However, Sandbox has only made an Alpha version available to the public.
Backing
The MANA vs SAND comparison would also include support for both platforms. Digital Currency Group, FBG Capital, and CoinFund are all supporters of Decentraland. It has also partnered with Polygon, the South Korean government, Cyberpunk, and Samsung.
SoftBank, a Japanese multinational conglomerate focused on investment management, is another major backer. Sandbox has the backing of one of the world's largest investment firms, as well as Slack and Uber.
Compatibility
Wallet compatibility is an important factor in comparing the two metaverse platforms. Decentraland currently has a competitive advantage. How? Both projects' marketplaces accept ERC-20 wallets. However, Decentraland has recently improved by bridging with Walletconnect. So it can let Polygon users join Decentraland.
Scalability
Because Sandbox and Decentraland use the Ethereum blockchain, scalability is an issue. Both platforms' scalability is constrained by volatile tokens and high gas fees. So, scalability issues can hinder large-scale adoption of both metaverse platforms.
Buying Land
Decentraland vs Sandbox comparisons often include virtual real estate. However, the ability to buy virtual land on both platforms defines the user experience and differentiates them. In this case, Sandbox offers better options for users to buy virtual land by combining OpenSea and Sandbox. In fact, Decentraland users can only buy from the MANA marketplace.
Innovation
The rate of development distinguishes Sandbox and Decentraland. Both platforms have been developing rapidly new features. However, Sandbox wins by adopting Polygon NFT layer 2 solutions, which consume almost 100 times less energy than Ethereum.
Collaborations
The platforms' collaborations are the key to determining "which is better Sandbox or Decentraland." Adoption of metaverse platforms like the two in question can be boosted by association with reputable brands. Among the partners are Atari, Cyberpunk, and Polygon. Rather, Sandbox has partnered with well-known brands like OpenSea, CryptoKitties, The Walking Dead, Snoop Dogg, and others.
Platform Adaptivity
Another key feature that distinguishes Sandbox and Decentraland is the ease of use. Sandbox clearly wins in terms of platform access. It allows easy access via social media, email, or a Metamask wallet. However, Decentraland requires a wallet connection.
Prospects
The future development plans also play a big role in defining Sandbox vs Decentraland. Sandbox's future development plans include bringing the platform to mobile devices. This includes consoles like PlayStation and Xbox. By the end of 2023, the platform expects to have around 5000 games.
Decentraland, on the other hand, has no set plan. In fact, the team defines the decisions that appear to have value. They plan to add celebrities, creators, and brands soon, along with NFT ads and drops.
Final Words
The comparison of Decentraland vs Sandbox provides a balanced view of both platforms. You can see how difficult it is to determine which decentralized metaverse is better now. Sandbox is still in Alpha, whereas Decentraland has a working proof of concept.
Sandbox, on the other hand, has better graphics and is backed by some big names. But both have a long way to go in the larger decentralized metaverse.
You might also like

VIP Graphics
3 years ago
Leaked pitch deck for Metas' new influencer-focused live-streaming service
As part of Meta's endeavor to establish an interactive live-streaming platform, the company is testing with influencers.
The NPE (new product experimentation team) has been testing Super since late 2020.

Bloomberg defined Super as a Cameo-inspired FaceTime-like gadget in 2020. The tool has evolved into a Twitch-like live streaming application.
Less than 100 creators have utilized Super: Creators can request access on Meta's website. Super isn't an Instagram, Facebook, or Meta extension.
“It’s a standalone project,” the spokesperson said about Super. “Right now, it’s web only. They have been testing it very quietly for about two years. The end goal [of NPE projects] is ultimately creating the next standalone project that could be part of the Meta family of products.” The spokesperson said the outreach this week was part of a drive to get more creators to test Super.
A 2021 pitch deck from Super reveals the inner workings of Meta.
The deck gathered feedback on possible sponsorship models, with mockups of brand deals & features. Meta reportedly paid creators $200 to $3,000 to test Super for 30 minutes.
Meta's pitch deck for Super live streaming was leaked.
What were the slides in the pitch deck for Metas Super?
Embed not supported: see full deck & article here →
View examples of Meta's pitch deck for Super:
Product Slides, first
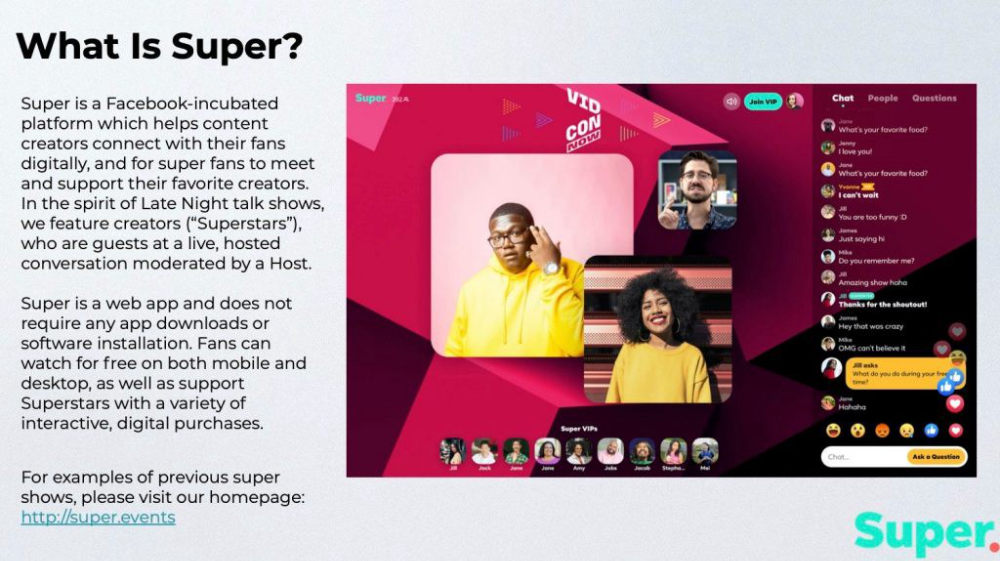
The pitch deck begins with Super's mission:
Super is a Facebook-incubated platform which helps content creators connect with their fans digitally, and for super fans to meet and support their favorite creators. In the spirit of Late Night talk shows, we feature creators (“Superstars”), who are guests at a live, hosted conversation moderated by a Host.
This slide (and most of the deck) is text-heavy, with few icons, bullets, and illustrations to break up the content. Super's online app status (which requires no download or installation) might be used as a callout (rather than paragraph-form).

Meta's Super platform focuses on brand sponsorships and native placements, as shown in the slide above.
One of our theses is the idea that creators should benefit monetarily from their Super experiences, and we believe that offering a menu of different monetization strategies will enable the right experience for each creator. Our current focus is exploring sponsorship opportunities for creators, to better understand what types of sponsor placements will facilitate the best experience for all Super customers (viewers, creators, and advertisers).
Colorful mockups help bring Metas vision for Super to life.
2. Slide Features
Super's pitch deck focuses on the platform's features. The deck covers pre-show, pre-roll, and post-event for a Sponsored Experience.
Pre-show: active 30 minutes before the show's start
Pre-roll: Play a 15-minute commercial for the sponsor before the event (auto-plays once)
Meet and Greet: This event can have a branding, such as Meet & Greet presented by [Snickers]
Super Selfies: Makers and followers get a digital souvenir to post on social media.
Post-Event: Possibility to draw viewers' attention to sponsored content/links during the after-show
Almost every screen displays the Sponsor logo, link, and/or branded background. Viewers can watch sponsor video while waiting for the event to start.
Slide 3: Business Model
Meta's presentation for Super is incomplete without numbers. Super's first slide outlines the creator, sponsor, and Super's obligations. Super does not charge creators any fees or commissions on sponsorship earnings.

How to make a great pitch deck
We hope you can use the Super pitch deck to improve your business. Bestpitchdeck.com/super-meta is a bookmarkable link.
You can also use one of our expert-designed templates to generate a pitch deck.
Our team has helped close $100M+ in agreements and funding for premier companies and VC firms. Use our presentation templates, one-pagers, or financial models to launch your pitch.
Every pitch must be audience-specific. Our team has prepared pitch decks for various sectors and fundraising phases.

Pitch Deck Software VIP.graphics produced a popular SaaS & Software Pitch Deck based on decks that closed millions in transactions & investments for orgs of all sizes, from high-growth startups to Fortune 100 enterprises. This easy-to-customize PowerPoint template includes ready-made features and key slides for your software firm.

Accelerator Pitch Deck The Accelerator Pitch Deck template is for early-stage founders seeking funding from pitch contests, accelerators, incubators, angels, or VC companies. Winning a pitch contest or getting into a top accelerator demands a strategic investor pitch.

Pitch Deck Template Series Startup and founder pitch deck template: Workable, smart slides. This pitch deck template is for companies, entrepreneurs, and founders raising seed or Series A finance.

M&A Pitch Deck Perfect Pitch Deck is a template for later-stage enterprises engaging more sophisticated conversations like M&A, late-stage investment (Series C+), or partnerships & funding. Our team prepared this presentation to help creators confidently pitch to investment banks, PE firms, and hedge funds (and vice versa).
Browse our growing variety of industry-specific pitch decks.

Startup Journal
3 years ago
The Top 14 Software Business Ideas That Are Sure To Succeed in 2023
Software can change any company.

Software is becoming essential. Everyone should consider how software affects their lives and others'.
Software on your phone, tablet, or computer offers many new options. We're experts in enough ways now.
Software Business Ideas will be popular by 2023.
ERP Programs
ERP software meets rising demand.
ERP solutions automate and monitor tasks that large organizations, businesses, and even schools would struggle to do manually.
ERP software could reach $49 billion by 2024.
CRM Program
CRM software is a must-have for any customer-focused business.
Having an open mind about your business services and products allows you to change platforms.
Another company may only want your CRM service.
Medical software
Healthcare facilities need reliable, easy-to-use software.
EHRs, MDDBs, E-Prescribing, and more are software options.
The global medical software market could reach $11 billion by 2025, and mobile medical apps may follow.
Presentation Software in the Cloud
SaaS presentation tools are great.
They're easy to use, comprehensive, and full of traditional Software features.
In today's cloud-based world, these solutions make life easier for people. We don't know about you, but we like it.
Software for Project Management
People began working remotely without signs or warnings before the 2020 COVID-19 pandemic.
Many organizations found it difficult to track projects and set deadlines.
With PMP software tools, teams can manage remote units and collaborate effectively.
App for Blockchain-Based Invoicing
This advanced billing and invoicing solution is for businesses and freelancers.
These blockchain-based apps can calculate taxes, manage debts, and manage transactions.
Intelligent contracts help blockchain track transactions more efficiently. It speeds up and improves invoice generation.
Software for Business Communications
Internal business messaging is tricky.
Top business software tools for communication can share files, collaborate on documents, host video conferences, and more.
Payroll Automation System
Software development also includes developing an automated payroll system.
These software systems reduce manual tasks for timely employee payments.
These tools help enterprise clients calculate total wages quickly, simplify tax calculations, improve record-keeping, and support better financial planning.
System for Detecting Data Leaks
Both businesses and individuals value data highly. Yahoo's data breach is dangerous because of this.
This area of software development can help people protect their data.
You can design an advanced data loss prevention system.
AI-based Retail System
AI-powered shopping systems are popular. The systems analyze customers' search and purchase patterns and store history and are equipped with a keyword database.
These systems offer many customers pre-loaded products.
AI-based shopping algorithms also help users make purchases.
Software for Detecting Plagiarism
Software can help ensure your projects are original and not plagiarized.
These tools detect plagiarized content that Google, media, and educational institutions don't like.
Software for Converting Audio to Text
Machine Learning converts speech to text automatically.
These programs can quickly transcribe cloud-based files.
Software for daily horoscopes
Daily and monthly horoscopes will continue to be popular.
Software platforms that can predict forecasts, calculate birth charts, and other astrology resources are good business ideas.
E-learning Programs
Traditional study methods are losing popularity as virtual schools proliferate and physical space shrinks.
Khan Academy online courses are the best way to keep learning.
Online education portals can boost your learning. If you want to start a tech startup, consider creating an e-learning program.
Conclusion
Software is booming. There's never been a better time to start a software development business, with so many people using computers and smartphones. This article lists eight business ideas for 2023. Consider these ideas if you're just starting out or looking to expand.
Scott Hickmann
3 years ago Draft
This is a draft

My wallpape

