More on Entrepreneurship/Creators

Jared Heyman
3 years ago
The survival and demise of Y Combinator startups
I've written a lot about Y Combinator's success, but as any startup founder or investor knows, many startups fail.
Rebel Fund invests in the top 5-10% of new Y Combinator startups each year, so we focus on identifying and supporting the most promising technology startups in our ecosystem. Given the power law dynamic and asymmetric risk/return profile of venture capital, we worry more about our successes than our failures. Since the latter still counts, this essay will focus on the proportion of YC startups that fail.
Since YC's launch in 2005, the figure below shows the percentage of active, inactive, and public/acquired YC startups by batch.
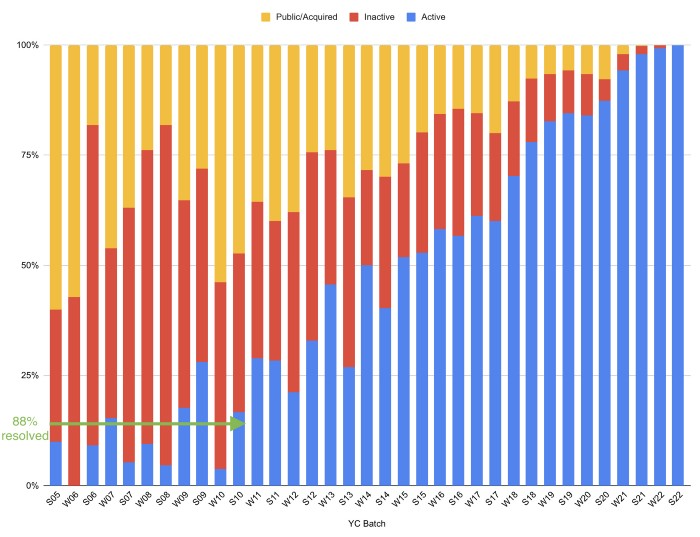
As more startups finish, the blue bars (active) decrease significantly. By 12 years, 88% of startups have closed or exited. Only 7% of startups reach resolution each year.
YC startups by status after 12 years:
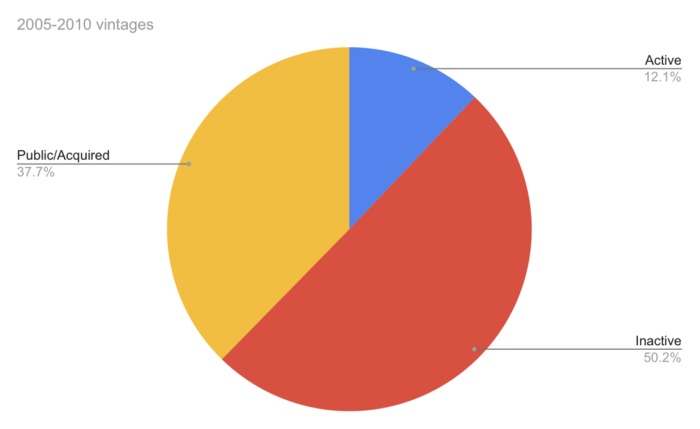
Half the startups have failed, over one-third have exited, and the rest are still operating.
In venture investing, it's said that failed investments show up before successful ones. This is true for YC startups, but only in their early years.
Below, we only present resolved companies from the first chart. Some companies fail soon after establishment, but after a few years, the inactive vs. public/acquired ratio stabilizes around 55:45. After a few years, a YC firm is roughly as likely to quit as fail, which is better than I imagined.
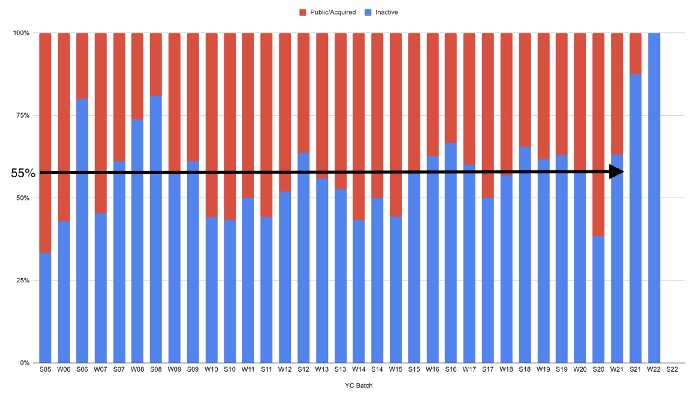
I prepared this post because Rebel investors regularly question me about YC startup failure rates and how long it takes for them to exit or shut down.
Early-stage venture investors can overlook it because 100x investments matter more than 0x investments.
YC founders can ignore it because it shouldn't matter if many of their peers succeed or fail ;)

Aaron Dinin, PhD
2 years ago
Are You Unintentionally Creating the Second Difficult Startup Type?
Most don't understand the issue until it's too late.

My first startup was what entrepreneurs call the hardest. A two-sided marketplace.
Two-sided marketplaces are the hardest startups because founders must solve the chicken or the egg conundrum.
A two-sided marketplace needs suppliers and buyers. Without suppliers, buyers won't come. Without buyers, suppliers won't come. An empty marketplace and a founder striving to gain momentum result.
My first venture made me a struggling founder seeking to achieve traction for a two-sided marketplace. The company failed, and I vowed never to start another like it.
I didn’t. Unfortunately, my second venture was almost as hard. It failed like the second-hardest startup.
What kind of startup is the second-hardest?
The second-hardest startup, which is almost as hard to develop, is rarely discussed in the startup community. Because of this, I predict more founders fail each year trying to develop the second-toughest startup than the hardest.
Fairly, I have no proof. I see many startups, so I have enough of firsthand experience. From what I've seen, for every entrepreneur developing a two-sided marketplace, I'll meet at least 10 building this other challenging startup.
I'll describe a startup I just met with its two co-founders to explain the second hardest sort of startup and why it's so hard. They created a financial literacy software for parents of high schoolers.
The issue appears plausible. Children struggle with money. Parents must teach financial responsibility. Problems?
It's possible.
Buyers and users are different.
Buyer-user mismatch.
The financial literacy app I described above targets parents. The parent doesn't utilize the app. Child is end-user. That may not seem like much, but it makes customer and user acquisition and onboarding difficult for founders.
The difficulty of a buyer-user imbalance
The company developing a product faces a substantial operational burden when the buyer and end customer are different. Consider classic firms where the buyer is the end user to appreciate that responsibility.
Entrepreneurs selling directly to end users must educate them about the product's benefits and use. Each demands a lot of time, effort, and resources.
Imagine selling a financial literacy app where the buyer and user are different. To make the first sale, the entrepreneur must establish all the items I mentioned above. After selling, the entrepreneur must supply a fresh set of resources to teach, educate, or train end-users.
Thus, a startup with a buyer-user mismatch must market, sell, and train two organizations at once, requiring twice the work with the same resources.
The second hardest startup is hard for reasons other than the chicken-or-the-egg conundrum. It takes a lot of creativity and luck to solve the chicken-or-egg conundrum.
The buyer-user mismatch problem cannot be overcome by innovation or luck. Buyer-user mismatches must be solved by force. Simply said, when a product buyer is different from an end-user, founders have a lot more work. If they can't work extra, their companies fail.

Keagan Stokoe
3 years ago
Generalists Create Startups; Specialists Scale Them
There’s a funny part of ‘Steve Jobs’ by Walter Isaacson where Jobs says that Bill Gates was more a copier than an innovator:
“Bill is basically unimaginative and has never invented anything, which is why I think he’s more comfortable now in philanthropy than technology. He just shamelessly ripped off other people’s ideas….He’d be a broader guy if he had dropped acid once or gone off to an ashram when he was younger.”
Gates lacked flavor. Nobody ever got excited about a Microsoft launch, despite their good products. Jobs had the world's best product taste. Apple vs. Microsoft.
A CEO's core job functions are all driven by taste: recruiting, vision, and company culture all require good taste. Depending on the type of company you want to build, know where you stand between Microsoft and Apple.
How can you improve your product judgment? How to acquire taste?

Test and refine
Product development follows two parallel paths: the ‘customer obsession’ path and the ‘taste and iterate’ path.
The customer obsession path involves solving customer problems. Lean Startup frameworks show you what to build at each step.
Taste-and-iterate doesn't involve the customer. You iterate internally and rely on product leaders' taste and judgment.
Creative Selection by Ken Kocienda explains this method. In Creative Selection, demos are iterated and presented to product leaders. Your boss presents to their boss, and so on up to Steve Jobs. If you have good product taste, you can be a panelist.
The iPhone follows this path. Before seeing an iPhone, consumers couldn't want one. Customer obsession wouldn't have gotten you far because iPhone buyers didn't know they wanted one.
In The Hard Thing About Hard Things, Ben Horowitz writes:
“It turns out that is exactly what product strategy is all about — figuring out the right product is the innovator’s job, not the customer’s job. The customer only knows what she thinks she wants based on her experience with the current product. The innovator can take into account everything that’s possible, but often must go against what she knows to be true. As a result, innovation requires a combination of knowledge, skill, and courage.“
One path solves a problem the customer knows they have, and the other doesn't. Instead of asking a person what they want, observe them and give them something they didn't know they needed.
It's much harder. Apple is the world's most valuable company because it's more valuable. It changes industries permanently.
If you want to build superior products, use the iPhone of your industry.
How to Improve Your Taste
I. Work for a company that has taste.
People with the best taste in products, markets, and people are rewarded for building great companies. Tasteful people know quality even when they can't describe it. Taste isn't writable. It's feel-based.
Moving into a community that's already doing what you want to do may be the best way to develop entrepreneurial taste. Most company-building knowledge is tacit.
Joining a company you want to emulate allows you to learn its inner workings. It reveals internal patterns intuitively. Many successful founders come from successful companies.
Consumption determines taste. Excellence will refine you. This is why restauranteurs visit the world's best restaurants and serious painters visit Paris or New York. Joining a company with good taste is beneficial.
2. Possess a wide range of interests
“Edwin Land of Polaroid talked about the intersection of the humanities and science. I like that intersection. There’s something magical about that place… The reason Apple resonates with people is that there’s a deep current of humanity in our innovation. I think great artists and great engineers are similar, in that they both have a desire to express themselves.” — Steve Jobs
I recently discovered Edwin Land. Jobs modeled much of his career after Land's. It makes sense that Apple was inspired by Land.
A Triumph of Genius: Edwin Land, Polaroid, and the Kodak Patent War notes:
“Land was introverted in person, but supremely confident when he came to his ideas… Alongside his scientific passions, lay knowledge of art, music, and literature. He was a cultured person growing even more so as he got older, and his interests filtered into the ethos of Polaroid.”
Founders' philosophies shape companies. Jobs and Land were invested. It showed in the products their companies made. Different. His obsession was spreading Microsoft software worldwide. Microsoft's success is why their products are bland and boring.
Experience is important. It's probably why startups are built by generalists and scaled by specialists.
Jobs combined design, typography, storytelling, and product taste at Apple. Some of the best original Mac developers were poets and musicians. Edwin Land liked broad-minded people, according to his biography. Physicist-musicians or physicist-photographers.
Da Vinci was a master of art, engineering, architecture, anatomy, and more. He wrote and drew at the same desk. His genius is remembered centuries after his death. Da Vinci's statue would stand at the intersection of humanities and science.
We find incredibly creative people here. Superhumans. Designers, creators, and world-improvers. These are the people we need to navigate technology and lead world-changing companies. Generalists lead.
You might also like

Julie Zhuo
2 years ago
Comparing poor and excellent managers
10-sketch explanation
Choosing Tasks


Bringing News


carrying out 1:1s

providing critique


Managing Turbulence



Jennifer Tieu
3 years ago
Why I Love Azuki
Azuki Banner (www.azuki.com)
Disclaimer: This is my personal viewpoint. I'm not on the Azuki team. Please keep in mind that I am merely a fan, community member, and holder. Please do your own research and pardon my grammar. Thanks!
Azuki has changed my view of NFTs.
When I first entered the NFT world, I had no idea what to expect. I liked the idea. So I invested in some projects, fought for whitelists, and discovered some cool NFTs projects (shout-out to CATC). I lost more money than I earned at one point, but I hadn't invested excessively (only put in what you can afford to lose). Despite my losses, I kept looking. I almost waited for the “ah-ha” moment. A NFT project that changed my perspective on NFTs. What makes an NFT project more than a work of art?
Answer: Azuki.
The Art
The Azuki art drew me in as an anime fan. It looked like something out of an anime, and I'd never seen it before in NFT.
The project was still new. The first two animated teasers were released with little fanfare, but I was impressed with their quality. You can find them on Instagram or in their earlier Tweets.
The teasers hinted that this project could be big and that the team could deliver. It was amazing to see Shao cut the Azuki posters with her katana. Especially at the end when she sheaths her sword and the music cues. Then the live action video of the young boy arranging the Azuki posters seemed movie-like. I felt like I was entering the Azuki story, brand, and dope theme.
The team did not disappoint with the Azuki NFTs. The level of detail in the art is stunning. There were Azukis of all genders, skin and hair types, and more. These 10,000 Azukis have so much representation that almost anyone can find something that resonates. Rather than me rambling on, I suggest you visit the Azuki gallery
The Team
If the art is meant to draw you in and be the project's face, the team makes it more. The NFT would be a JPEG without a good team leader. Not that community isn't important, but no community would rally around a bad team.
Because I've been rugged before, I'm very focused on the team when considering a project. While many project teams are anonymous, I try to find ones that are doxxed (public) or at least appear to be established. Unlike Azuki, where most of the Azuki team is anonymous, Steamboy is public. He is (or was) Overwatch's character art director and co-creator of Azuki. I felt reassured and could trust the project after seeing someone from a major game series on the team.
Then I tried to learn as much as I could about the team. Following everyone on Twitter, reading their tweets, and listening to recorded AMAs. I was impressed by the team's professionalism and dedication to their vision for Azuki, led by ZZZAGABOND.
I believe the phrase “actions speak louder than words” applies to Azuki. I can think of a few examples of what the Azuki team has done, but my favorite is ERC721A.
With ERC721A, Azuki has created a new algorithm that allows minting multiple NFTs for essentially the same cost as minting one NFT.
I was ecstatic when the dev team announced it. This fascinates me as a self-taught developer. Azuki released a product that saves people money, improves the NFT space, and is open source. It showed their love for Azuki and the NFT community.
The Community
Community, community, community. It's almost a chant in the NFT space now. A community, like a team, can make or break a project. We are the project's consumers, shareholders, core, and lifeblood. The team builds the house, and we fill it. We stay for the community.
When I first entered the Azuki Discord, I was surprised by the calm atmosphere. There was no news about the project. No release date, no whitelisting requirements. No grinding or spamming either. People just wanted to hangout, get to know each other, and talk. It was nice. So the team could pick genuine people for their mintlist (aka whitelist).
But nothing fundamental has changed since the release. It has remained an authentic, fun, and helpful community. I'm constantly logging into Discord to chat with others or follow conversations. I see the community's openness to newcomers. Everyone respects each other (barring a few bad apples) and the variety of people passing through is fascinating. This human connection and interaction is what I enjoy about this place. Being a part of a group that supports a cause.
Finally, I want to thank the amazing Azuki mod team and the kissaten channel for their contributions.
The Brand
So, what sets Azuki apart from other projects? They are shaping a brand or identity. The Azuki website, I believe, best captures their vision. (This is me gushing over the site.)
If you go to the website, turn on the dope playlist in the bottom left. The playlist features a mix of Asian and non-Asian hip-hop and rap artists, with some lo-fi thrown in. The songs on the playlist change, but I think you get the vibe Azuki embodies just by turning on the music.
The Garden is our next stop where we are introduced to Azuki.
A brand.
We're creating a new brand together.
A metaverse brand. By the people.
A collection of 10,000 avatars that grant Garden membership. It starts with exclusive streetwear collabs, NFT drops, live events, and more. Azuki allows for a new media genre that the world has yet to discover. Let's build together an Azuki, your metaverse identity.
The Garden is a magical internet corner where art, community, and culture collide. The boundaries between the physical and digital worlds are blurring.
Try a Red Bean.
The text begins with Azuki's intention in the space. It's a community-made metaverse brand. Then it goes into more detail about Azuki's plans. Initiation of a story or journey. "Would you like to take the red bean and jump down the rabbit hole with us?" I love the Matrix red pill or blue pill play they used. (Azuki in Japanese means red bean.)
Morpheus, the rebel leader, offers Neo the choice of a red or blue pill in The Matrix. “You take the blue pill... After the story, you go back to bed and believe whatever you want. Your red pill... Let me show you how deep the rabbit hole goes.” Aware that the red pill will free him from the enslaving control of the machine-generated dream world and allow him to escape into the real world, he takes it. However, living the “truth of reality” is harsher and more difficult.
It's intriguing and draws you in. Taking the red bean causes what? Where am I going? I think they did well in piqueing a newcomer's interest.
Not convinced by the Garden? Read the Manifesto. It reinforces Azuki's role.
Here comes a new wave…
And surfing here is different.
Breaking down barriers.
Building open communities.
Creating magic internet money with our friends.
To those who don’t get it, we tell them: gm.
They’ll come around eventually.
Here’s to the ones with the courage to jump down a peculiar rabbit hole.
One that pulls you away from a world that’s created by many and owned by few…
To a world that’s created by more and owned by all.
From The Garden come the human beans that sprout into your family.
We rise together.
We build together.
We grow together.
Ready to take the red bean?
Not to mention the Mindmap, it sets Azuki apart from other projects and overused Roadmaps. I like how the team recognizes that the NFT space is not linear. So many of us are still trying to figure it out. It is Azuki's vision to adapt to changing environments while maintaining their values. I admire their commitment to long-term growth.
Conclusion
To be honest, I have no idea what the future holds. Azuki is still new and could fail. But I'm a long-term Azuki fan. I don't care about quick gains. The future looks bright for Azuki. I believe in the team's output. I love being an Azuki.
Thank you! IKUZO!
Full post here

Enrique Dans
2 years ago
What happens when those without morals enter the economic world?

I apologize if this sounds basic, but throughout my career, I've always been clear that a company's activities are shaped by its founder(s)' morality.
I consider Palantir, owned by PayPal founder Peter Thiel, evil. He got $5 billion tax-free by hacking a statute to help middle-class savings. That may appear clever, but I think it demonstrates a shocking lack of solidarity with society. As a result of this and other things he has said and done, I early on dismissed Peter Thiel as someone who could contribute anything positive to society, and events soon proved me right: we are talking about someone who clearly considers himself above everyone else and who does not hesitate to set up a company, Palantir, to exploit the data of the little people and sell it to the highest bidder, whoever that is and whatever the consequences.
The German courts have confirmed my warnings concerning Palantir. The problem is that politicians love its surveillance tools because they think knowing more about their constituents gives them power. These are ideal for dictatorships who want to snoop on their populace. Hence, Silicon Valley's triumphalist dialectic has seduced many governments at many levels and collected massive volumes of data to hold forever.
Dangerous company. There are many more. My analysis of the moral principles that disclose company management changed my opinion of Facebook, now Meta, and anyone with a modicum of interest might deduce when that happened, a discovery that leaves you dumbfounded. TikTok was easy because its lack of morality was revealed early when I saw the videos it encouraged minors to post and the repercussions of sharing them through its content recommendation algorithm. When you see something like this, nothing can convince you that the firm can change its morals and become good. Nothing. You know the company is awful and will fail. Speak it, announce it, and change it. It's like a fingerprint—unchangeable.
Some of you who read me frequently make its Facebook today jokes when I write about these firms, and that's fine: they're my moral standards, those of an elderly professor with thirty-five years of experience studying corporations and discussing their cases in class, but you don't have to share them. Since I'm writing this and don't have to submit to any editorial review, that's what it is: when you continuously read a person, you have to assume that they have moral standards and that sometimes you'll agree with them and sometimes you won't. Morality accepts hierarchies, nuances, and even obsessions. I know not everyone shares my opinions, but at least I can voice them. One day, one of those firms may sue me (as record companies did some years ago).
Palantir is incredibly harmful. Limit its operations. Like Meta and TikTok, its business strategy is shaped by its founders' immorality. Such a procedure can never be beneficial.
