An approximate introduction to how zk-SNARKs are possible (part 2)
If tasked with the problem of coming up with a zk-SNARK protocol, many people would make their way to this point and then get stuck and give up. How can a verifier possibly check every single piece of the computation, without looking at each piece of the computation individually? But it turns out that there is a clever solution.
Polynomials
Polynomials are a special class of algebraic expressions of the form:
- x+5
- x^4
- x^3+3x^2+3x+1
- 628x^{271}+318x^{270}+530x^{269}+…+69x+381
i.e. they are a sum of any (finite!) number of terms of the form cx^k
There are many things that are fascinating about polynomials. But here we are going to zoom in on a particular one: polynomials are a single mathematical object that can contain an unbounded amount of information (think of them as a list of integers and this is obvious). The fourth example above contained 816 digits of tau, and one can easily imagine a polynomial that contains far more.
Furthermore, a single equation between polynomials can represent an unbounded number of equations between numbers. For example, consider the equation A(x)+ B(x) = C(x). If this equation is true, then it's also true that:
- A(0)+B(0)=C(0)
- A(1)+B(1)=C(1)
- A(2)+B(2)=C(2)
- A(3)+B(3)=C(3)
And so on for every possible coordinate. You can even construct polynomials to deliberately represent sets of numbers so you can check many equations all at once. For example, suppose that you wanted to check:
- 12+1=13
- 10+8=18
- 15+8=23
- 15+13=28
You can use a procedure called Lagrange interpolation to construct polynomials A(x) that give (12,10,15,15) as outputs at some specific set of coordinates (eg. (0,1,2,3)), B(x) the outputs (1,8,8,13) on thos same coordinates, and so forth. In fact, here are the polynomials:
- A(x)=-2x^3+\frac{19}{2}x^2-\frac{19}{2}x+12
- B(x)=2x^3-\frac{19}{2}x^2+\frac{29}{2}x+1
- C(x)=5x+13
Checking the equation A(x)+B(x)=C(x) with these polynomials checks all four above equations at the same time.
Comparing a polynomial to itself
You can even check relationships between a large number of adjacent evaluations of the same polynomial using a simple polynomial equation. This is slightly more advanced. Suppose that you want to check that, for a given polynomial F, F(x+2)=F(x)+F(x+1) with the integer range {0,1…89} (so if you also check F(0)=F(1)=1, then F(100) would be the 100th Fibonacci number)
As polynomials, F(x+2)-F(x+1)-F(x) would not be exactly zero, as it could give arbitrary answers outside the range x={0,1…98}. But we can do something clever. In general, there is a rule that if a polynomial P is zero across some set S=\{x_1,x_2…x_n\} then it can be expressed as P(x)=Z(x)*H(x), where Z(x)=(x-x_1)*(x-x_2)*…*(x-x_n) and H(x) is also a polynomial. In other words, any polynomial that equals zero across some set is a (polynomial) multiple of the simplest (lowest-degree) polynomial that equals zero across that same set.
Why is this the case? It is a nice corollary of polynomial long division: the factor theorem. We know that, when dividing P(x) by Z(x), we will get a quotient Q(x) and a remainder R(x) is strictly less than that of Z(x). Since we know that P is zero on all of S, it means that R has to be zero on all of S as well. So we can simply compute R(x) via polynomial interpolation, since it's a polynomial of degree at most n-1 and we know n values (the zeros at S). Interpolating a polynomial with all zeroes gives the zero polynomial, thus R(x)=0 and H(x)=Q(x).
Going back to our example, if we have a polynomial F that encodes Fibonacci numbers (so F(x+2)=F(x)+F(x+1) across x=\{0,1…98\}), then I can convince you that F actually satisfies this condition by proving that the polynomial P(x)=F(x+2)-F(x+1)-F(x) is zero over that range, by giving you the quotient:
H(x)=\frac{F(x+2)-F(x+1)-F(x)}{Z(x)}
Where Z(x) = (x-0)*(x-1)*…*(x-98).
You can calculate Z(x) yourself (ideally you would have it precomputed), check the equation, and if the check passes then F(x) satisfies the condition!
Now, step back and notice what we did here. We converted a 100-step-long computation into a single equation with polynomials. Of course, proving the N'th Fibonacci number is not an especially useful task, especially since Fibonacci numbers have a closed form. But you can use exactly the same basic technique, just with some extra polynomials and some more complicated equations, to encode arbitrary computations with an arbitrarily large number of steps.
see part 3
(Edited)

Hackernoon
4 years ago
👏 Awesome post! When is part 3 coming?

Trent Lapinski
4 years ago
Very complex topic, great explanation
More on Web3 & Crypto

Faisal Khan
2 years ago
4 typical methods of crypto market manipulation

Market fraud
Due to its decentralized and fragmented character, the crypto market has integrity difficulties.
Cryptocurrencies are an immature sector, therefore market manipulation becomes a bigger issue. Many research have attempted to uncover these abuses. CryptoCompare's newest one highlights some of the industry's most typical scams.
Why are these concerns so common in the crypto market? First, even the largest centralized exchanges remain unregulated due to industry immaturity. A low-liquidity market segment makes an attack more harmful. Finally, market surveillance solutions not implemented reduce transparency.
In CryptoCompare's latest exchange benchmark, 62.4% of assessed exchanges had a market surveillance system, although only 18.1% utilised an external solution. To address market integrity, this measure must improve dramatically. Before discussing the report's malpractices, note that this is not a full list of attacks and hacks.
Clean Trading
An investor buys and sells concurrently to increase the asset's price. Centralized and decentralized exchanges show this misconduct. 23 exchanges have a volume-volatility correlation < 0.1 during the previous 100 days, according to CryptoCompares. In August 2022, Exchange A reported $2.5 trillion in artificial and/or erroneous volume, up from $33.8 billion the month before.
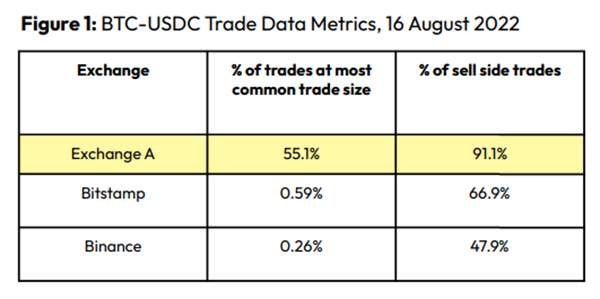
Spoofing
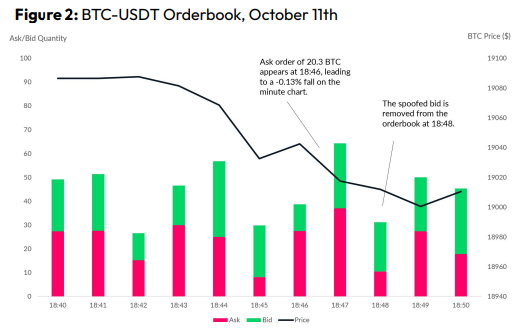
Criminals create and cancel fake orders before they can be filled. Since manipulators can hide in larger trading volumes, larger exchanges have more spoofing. A trader placed a 20.8 BTC ask order at $19,036 when BTC was trading at $19,043. BTC declined 0.13% to $19,018 in a minute. At 18:48, the trader canceled the ask order without filling it.
Front-Running
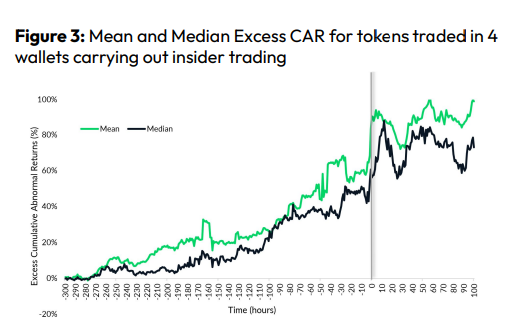
Most cryptocurrency front-running involves inside trading. Traditional stock markets forbid this. Since most digital asset information is public, this is harder. Retailers could utilize bots to front-run.
CryptoCompare found digital wallets of people who traded like insiders on exchange listings. The figure below shows excess cumulative anomalous returns (CAR) before a coin listing on an exchange.
Finally, LAYERING is a sequence of spoofs in which successive orders are put along a ladder of greater (layering offers) or lower (layering bids) values. The paper concludes with recommendations to mitigate market manipulation. Exchange data transparency, market surveillance, and regulatory oversight could reduce manipulative tactics.
Alex Bentley
3 years ago
Why Bill Gates thinks Bitcoin, crypto, and NFTs are foolish
Microsoft co-founder Bill Gates assesses digital assets while the bull is caged.

Bill Gates is well-respected.
Reasonably. He co-founded and led Microsoft during its 1980s and 1990s revolution.
After leaving Microsoft, Bill Gates pursued other interests. He and his wife founded one of the world's largest philanthropic organizations, Bill & Melinda Gates Foundation. He also supports immunizations, population control, and other global health programs.
When Gates criticized Bitcoin, cryptocurrencies, and NFTs, it made news.
Bill Gates said at the 58th Munich Security Conference...
“You have an asset class that’s 100% based on some sort of greater fool theory that somebody’s going to pay more for it than I do.”
Gates means digital assets. Like many bitcoin critics, he says digital coins and tokens are speculative.
And he's not alone. Financial experts have dubbed Bitcoin and other digital assets a "bubble" for a decade.
Gates also made fun of Bored Ape Yacht Club and NFTs, saying, "Obviously pricey digital photographs of monkeys will help the world."
Why does Bill Gates dislike digital assets?
According to Gates' latest comments, Bitcoin, cryptos, and NFTs aren't good ways to hold value.
Bill Gates is a better investor than Elon Musk.
“I’m used to asset classes, like a farm where they have output, or like a company where they make products,” Gates said.
The Guardian claimed in April 2021 that Bill and Melinda Gates owned the most U.S. farms. Over 242,000 acres of farmland.
The Gates couple has enough farmland to cover Hong Kong.

Bill Gates is a classic investor. He wants companies with an excellent track record, strong fundamentals, and good management. Or tangible assets like land and property.
Gates prefers the "old economy" over the "new economy"
Gates' criticism of Bitcoin and cryptocurrency ventures isn't surprising. These digital assets lack all of Gates's investing criteria.
Volatile digital assets include Bitcoin. Their costs might change dramatically in a day. Volatility scares risk-averse investors like Gates.
Gates has a stake in the old financial system. As Microsoft's co-founder, Gates helped develop a dominant tech company.
Because of his business, he's one of the world's richest men.
Bill Gates is invested in protecting the current paradigm.
He won't invest in anything that could destroy the global economy.
When Gates criticizes Bitcoin, cryptocurrencies, and NFTs, he's suggesting they're a hoax. These soapbox speeches are one way he protects his interests.
Digital assets aren't a bad investment, though. Many think they're the future.
Changpeng Zhao and Brian Armstrong are two digital asset billionaires. Two crypto exchange CEOs. Binance/Coinbase.
Digital asset revolution won't end soon.
If you disagree with Bill Gates and plan to invest in Bitcoin, cryptocurrencies, or NFTs, do your own research and understand the risks.
But don’t take Bill Gates’ word for it.
He’s just an old rich guy with a lot of farmland.
He has a lot to lose if Bitcoin and other digital assets gain global popularity.
This post is a summary. Read the full article here.

Nitin Sharma
3 years ago
Web3 Terminology You Should Know
The easiest online explanation.

Web3 is growing. Crypto companies are growing.
Instagram, Adidas, and Stripe adopted cryptocurrency.

Bitcoin and other cryptocurrencies made web3 famous.
Most don't know where to start. Cryptocurrency, DeFi, etc. are investments.
Since we don't understand web3, I'll help you today.
Let’s go.
1. Web3
It is the third generation of the web, and it is built on the decentralization idea which means no one can control it.
There are static webpages that we can only read on the first generation of the web (i.e. Web 1.0).
Web 2.0 websites are interactive. Twitter, Medium, and YouTube.
Each generation controlled the website owner. Simply put, the owner can block us. However, data breaches and selling user data to other companies are issues.
They can influence the audience's mind since they have control.
Assume Twitter's CEO endorses Donald Trump. Result? Twitter would have promoted Donald Trump with tweets and graphics, enhancing his chances of winning.
We need a decentralized, uncontrollable system.
And then there’s Web3.0 to consider. As Bitcoin and Ethereum values climb, so has its popularity. Web3.0 is uncontrolled web evolution. It's good and bad.
Dapps, DeFi, and DAOs are here. It'll all be explained afterwards.
2. Cryptocurrencies:
No need to elaborate.
Bitcoin, Ethereum, Cardano, and Dogecoin are cryptocurrencies. It's digital money used for payments and other uses.
Programs must interact with cryptocurrencies.
3. Blockchain:
Blockchain facilitates bitcoin transactions, investments, and earnings.
This technology governs Web3. It underpins the web3 environment.
Let us delve much deeper.
Blockchain is simple. However, the name expresses the meaning.
Blockchain is a chain of blocks.
Let's use an image if you don't understand.
The graphic above explains blockchain. Think Blockchain. The block stores related data.
Here's more.
4. Smart contracts
Programmers and developers must write programs. Smart contracts are these blockchain apps.
That’s reasonable.
Decentralized web3.0 requires immutable smart contracts or programs.
5. NFTs
Blockchain art is NFT. Non-Fungible Tokens.
Explaining Non-Fungible Token may help.
Two sorts of tokens:
These tokens are fungible, meaning they can be changed. Think of Bitcoin or cash. The token won't change if you sell one Bitcoin and acquire another.
Non-Fungible Token: Since these tokens cannot be exchanged, they are exclusive. For instance, music, painting, and so forth.
Right now, Companies and even individuals are currently developing worthless NFTs.
The concept of NFTs is much improved when properly handled.
6. Dapp
Decentralized apps are Dapps. Instagram, Twitter, and Medium apps in the same way that there is a lot of decentralized blockchain app.
Curve, Yearn Finance, OpenSea, Axie Infinity, etc. are dapps.
7. DAOs
DAOs are member-owned and governed.
Consider it a company with a core group of contributors.
8. DeFi
We all utilize centrally regulated financial services. We fund these banks.
If you have $10,000 in your bank account, the bank can invest it and retain the majority of the profits.
We only get a penny back. Some banks offer poor returns. To secure a loan, we must trust the bank, divulge our information, and fill out lots of paperwork.
DeFi was built for such issues.
Decentralized banks are uncontrolled. Staking, liquidity, yield farming, and more can earn you money.
Web3 beginners should start with these resources.
You might also like

William Anderson
3 years ago
When My Remote Leadership Skills Took Off
4 Ways To Manage Remote Teams & Employees
The wheels hit the ground as I landed in Rochester.
Our six-person satellite office was now part of my team.
Their manager only reported to me the day before, but I had my ticket booked ahead of time.
I had managed remote employees before but this was different. Engineers dialed into headquarters for every meeting.
So when I learned about the org chart change, I knew a strong first impression would set the tone for everything else.
I was either their boss, or their boss's boss, and I needed them to know I was committed.
Managing a fleet of satellite freelancers or multiple offices requires treating others as more than just a face behind a screen.
You must comprehend each remote team member's perspective and daily interactions.
The good news is that you can start using these techniques right now to better understand and elevate virtual team members.
1. Make Visits To Other Offices
If budgeted, visit and work from offices where teams and employees report to you. Only by living alongside them can one truly comprehend their problems with communication and other aspects of modern life.
2. Have Others Come to You
• Having remote, distributed, or satellite employees and teams visit headquarters every quarter or semi-quarterly allows the main office culture to rub off on them.
When remote team members visit, more people get to meet them, which builds empathy.
If you can't afford to fly everyone, at least bring remote managers or leaders. Hopefully they can resurrect some culture.
3. Weekly Work From Home
No home office policy?
Make one.
WFH is a team-building, problem-solving, and office-viewing opportunity.
For dial-in meetings, I started working from home on occasion.
It also taught me which teams “forget” or “skip” calls.
As a remote team member, you experience all the issues first hand.
This isn't as accurate for understanding teams in other offices, but it can be done at any time.
4. Increase Contact Even If It’s Just To Chat
Don't underestimate office banter.
Sometimes it's about bonding and trust, other times it's about business.
If you get all this information in real-time, please forward it.
Even if nothing critical is happening, call remote team members to check in and chat.
I guarantee that building relationships and rapport will increase both their job satisfaction and yours.

Al Anany
3 years ago
Notion AI Might Destroy Grammarly and Jasper
The trick Notion could use is simply Facebook-ing the hell out of them.

*Time travel to fifteen years ago.* Future-Me: “Hey! What are you up to?” Old-Me: “I am proofreading an article. It’s taking a few hours, but I will be done soon.” Future-Me: “You know, in the future, you will be using a google chrome plugin called Grammarly that will help you easily proofread articles in half that time.” Old-Me: “What is… Google Chrome?” Future-Me: “Gosh…”
I love Grammarly. It’s one of those products that I personally feel the effects of. I mean, Space X is a great company. But I am not a rocket writing this article in space (or am I?)…
No, I’m not. So I don’t personally feel a connection to Space X. So, if a company collapse occurs in the morning, I might write about it. But I will have zero emotions regarding it.
Yet, if Grammarly fails tomorrow, I will feel 1% emotionally distressed. So looking at the title of this article, you’d realize that I am betting against them. This is how much I believe in the critical business model that’s taking over the world, the one of Notion.
Notion How frequently do you go through your notes?
Grammarly is everywhere, which helps its success. Grammarly is available when you update LinkedIn on Chrome. Grammarly prevents errors in Google Docs.
My internal concentration isn't apparent in the previous paragraph. Not Grammarly. I should have used Chrome to make a Google doc and LinkedIn update. Without this base, Grammarly will be useless.
So, welcome to this business essay.
Grammarly provides a solution.
Another issue is resolved by Jasper.
Your entire existence is supposed to be contained within Notion.
New Google Chrome is offline. It's an all-purpose notepad (in the near future.)
How should I start my blog? Enter it in Note.
an update on LinkedIn? If you mention it, it might be automatically uploaded there (with little help from another app.)
An advanced thesis? You can brainstorm it with your coworkers.
This ad sounds great! I won't cry if Notion dies tomorrow.
I'll reread the following passages to illustrate why I think Notion could kill Grammarly and Jasper.
Notion is a fantastic app that incubates your work.
Smartly, they began with note-taking.
Hopefully, your work will be on Notion. Grammarly and Jasper are still must-haves.
Grammarly will proofread your typing while Jasper helps with copywriting and AI picture development.
They're the best, therefore you'll need them. Correct? Nah.
Notion might bombard them with Facebook posts.
Notion: “Hi Grammarly, do you want to sell your product to us?” Grammarly: “Dude, we are more valuable than you are. We’ve even raised $400m, while you raised $342m. Our last valuation round put us at $13 billion, while yours put you at $10 billion. Go to hell.” Notion: “Okay, we’ll speak again in five years.”
Notion: “Jasper, wanna sell?” Jasper: “Nah, we’re deep into AI and the field. You can’t compete with our people.” Notion: “How about you either sell or you turn into a Snapchat case?” Jasper: “…”
Notion is your home. Grammarly is your neighbor. Your track is Jasper.
What if you grew enough vegetables in your backyard to avoid the supermarket? No more visits.
What if your home had a beautiful treadmill? You won't rush outside as much (I disagree with my own metaphor). (You get it.)
It's Facebooking. Instagram Stories reduced your Snapchat usage. Notion will reduce your need to use Grammarly.
The Final Piece of the AI Puzzle
Let's talk about Notion first, since you've probably read about it everywhere.
They raised $343 million, as I previously reported, and bought four businesses
According to Forbes, Notion will have more than 20 million users by 2022. The number of users is up from 4 million in 2020.
If raising $1.8 billion was impressive, FTX wouldn't have fallen.
This article compares the basic product to two others. Notion is a day-long app.
Notion has released Notion AI to support writers. It's early, so it's not as good as Jasper. Then-Jasper isn't now-Jasper. In five years, Notion AI will be different.
With hard work, they may construct a Jasper-like writing assistant. They have resources and users.
At this point, it's all speculation. Jasper's copywriting is top-notch. Grammarly's proofreading is top-notch. Businesses are constrained by user activities.
If Notion's future business movements are strategic, they might become a blue ocean shark (or get acquired by an unbelievable amount.)
I love business mental teasers, so tell me:
How do you feel? Are you a frequent Notion user?
Do you dispute my position? I enjoy hearing opposing viewpoints.
Ironically, I proofread this with Grammarly.

Luke Plunkett
3 years ago
Gran Turismo 7 Update Eases Up On The Grind After Fan Outrage
Polyphony Digital has changed the game after apologizing in March.
To make amends for some disastrous downtime, Gran Turismo 7 director Kazunori Yamauchi announced a credits handout and promised to “dramatically change GT7's car economy to help make amends” last month. The first of these has arrived.
The game's 1.11 update includes the following concessions to players frustrated by the economy and its subsequent grind:
-
The last half of the World Circuits events have increased in-game credit rewards.
-
Modified Arcade and Custom Race rewards
-
Clearing all circuit layouts with Gold or Bronze now rewards In-game Credits. Exiting the Sector selection screen with the Exit button will award Credits if an event has already been cleared.
-
Increased Credits Rewards in Lobby and Daily Races
-
Increased the free in-game Credits cap from 20,000,000 to 100,000,000.
Additionally, “The Human Comedy” missions are one-hour endurance races that award “up to 1,200,000” credits per event.
This isn't everything Yamauchi promised last month; he said it would take several patches and updates to fully implement the changes. Here's a list of everything he said would happen, some of which have already happened (like the World Cup rewards and credit cap):
- Increase rewards in the latter half of the World Circuits by roughly 100%.
- Added high rewards for all Gold/Bronze results clearing the Circuit Experience.
- Online Races rewards increase.
- Add 8 new 1-hour Endurance Race events to Missions. So expect higher rewards.
- Increase the non-paid credit limit in player wallets from 20M to 100M.
- Expand the number of Used and Legend cars available at any time.
- With time, we will increase the payout value of limited time rewards.
- New World Circuit events.
- Missions now include 24-hour endurance races.
- Online Time Trials added, with rewards based on the player's time difference from the leader.
- Make cars sellable.
The full list of updates and changes can be found here.
Read the original post.
