Prudence is advised. Be debt-free. Be frugal. Spend less.

This advice sounds nice, but it rarely works.

Most people never learn these two money rules. Both approaches will impact how you see personal finance.

It may safeguard you from inflation or the inability to preserve money.

Let’s dive in.

#1: Making long-term debt your ally

High-interest debt hurts consumers. Many credit cards carry 25% yearly interest (or more), so always pay on time. Otherwise, you’re losing money.

Some low-interest debt is good. Especially when buying an appreciating asset with borrowed money.

Inflation helps you.

If you borrow $800,000 at 3% interest and invest it at 7%, you'll make $32,000 (4%).

As money loses value, fixed payments get cheaper. Your assets' value and cash flow rise.

The never-in-debt crowd doesn't know this. They lose money paying off mortgages and low-interest loans early when they could have bought assets instead.

#2: How To Buy Or Build Assets To Make Inflation Irrelevant

Dozens of studies demonstrate actual wage growth is static; $2.50 in 1964 was equivalent to $22.65 now.

These reports never give solutions unless they're selling gold.

But there is one.

Assets beat inflation.

$100 invested into the S&P 500 would have an inflation-adjusted return of 17,739.30%.

Likewise, you can build assets from nothing.  Doing is easy and quick. The returns can boost your income by 10% or more.

The people who obsess over inflation inadvertently make the problem worse for themselves.  They wait for The Big Crash to buy assets. Or they moan about debt clocks and spending bills instead of seeking a solution.

Conclusion

Being ultra-prudent is like playing golf with a putter to avoid hitting the ball into the water. Sure, you might not slice a drive into the pond. But, you aren’t going to play well either. Or have very much fun.

Money has rules.

Avoiding debt or investment risks will limit your rewards. Long-term, being too cautious hurts your finances.

Disclaimer: This article is for entertainment purposes only. It is not financial advice, always do your own research.

Calmness is a vital life skill.

It aids communication. It boosts creativity and performance.

I've studied calm people's habits for years. Commonalities:

Have learned to laugh at themselves.

Those who have something to protect can’t help but make it a very serious business, which drains the energy out of the room.

They are fixated on positive pursuits like making cool things, building a strong physique, and having fun with others rather than on depressing influences like the news and gossip.

Every day, spend at least 20 minutes moving, whether it's walking, yoga, or lifting weights.

Discover ways to take pleasure in life's challenges.

Since perspective is malleable, they change their view.

Set your own needs first.

Stressed people neglect themselves and wonder why they struggle.

Prioritize self-care.

Don't ruin your life to please others.

Make something.

Calm people create more than react.

They love creating beautiful things—paintings, children, relationships, and projects.

Hold your breath, please.

If you're stressed or angry, you may be surprised how much time you spend holding your breath and tightening your belly.

Release, breathe, and relax to find calm.

Stopped rushing.

Rushing is disadvantageous.

Calm people handle life better.

Are attuned to their personal dietary needs.

They avoid junk food and eat foods that keep them healthy, happy, and calm.

Don’t take anything personally.

Stressed people control everything.

Self-conscious.

Calm people put others and their work first.

Keep their surroundings neat.

Maintaining an uplifting and clutter-free environment daily calms the mind.

Minimise negative people.

Calm people are ruthless with their boundaries and avoid negative and drama-prone people.

Restructuring and layoffs cause career reevaluation. Your career can benefit.

Once you become institutionalized, the corporate ladder is all you know.

You're bubbled. Extremists term it the corporate Matrix. I'm not so severe because the business world brainwashed me, too.

This boosted my corporate career.

Until I hit bottom.

15 months later, I view my corporate life differently. You may wish to advance professionally. Read this before you do.

Your happiness in the workplace may be deceptive.

I've been fortunate to spend time with corporate aces.

Working for 2.5 years in banking social media gave me some of these experiences. Earlier in my career, I recorded interviews with business leaders.

These people have titles like Chief General Manager and Head Of. New titles brought life-changing salaries.

They seemed happy.

I’d pass them in the hallway and they’d smile or shake my hand. I dreamt of having their life.

The ominous pattern

Unfiltered talks with some of them revealed a different world.

They acted well. They were skilled at smiling and saying the correct things. All had the same dark pattern, though.

Something felt off.

I found my conversations with them were generally for their benefit. They hoped my online antics as a writer/coach would shed light on their dilemma.

They'd tell me they wanted more. When you're one position away from CEO, it's hard not to wonder if this next move will matter.

What really displeased corporate ladder chasers

Before ascending further, consider these.

Zero autonomy

As you rise in a company, your days get busier.

Many people and initiatives need supervision. Everyone expects you to know business details. Weak when you don't. A poor leader is fired during the next restructuring and left to pursue their corporate ambition.

Full calendars leave no time for reflection. You can't have a coffee with a friend or waste a day.

You’re always on call. It’s a roll call kinda life.

Unable to express oneself freely

My 8 years of LinkedIn writing helped me meet these leaders.

I didn't think they'd care. Mistake.

Corporate leaders envied me because they wanted to talk freely again without corporate comms or a PR firm directing them what to say.

They couldn't share their flaws or inspiring experiences.

They wanted to.

Every day they were muzzled eroded by their business dream.

Limited family time

Top leaders had families.

They've climbed the corporate ladder. Nothing excellent happens overnight.

Corporate dreamers rarely saw their families.

Late meetings, customer functions, expos, training, leadership days, team days, town halls, and product demos regularly occurred after work.

Or they had to travel interstate or internationally for work events. They used bags and motel showers.

Initially, they said business class flights and hotels were nice. They'd get bored. 5-star hotels become monotonous.

No hotel beats home.

One leader said he hadn't seen his daughter much. They used to Facetime, but now that he's been gone so long, she rarely wants to talk to him.

So they iPad-parented.

You're miserable without your family.

Held captive by other job titles

Going up the business ladder seems like a battle.

Leaders compete for business gains and corporate advancement.

I saw shocking filthy tricks. Leaders would lie to seem nice.

Captives included top officials.

A different section every week. If they ran technology, the Head of Sales would argue their CRM cost millions. Or an Operations chief would battle a product team over support requests.

After one conflict, another began.

Corporate echelons are antagonistic. Huge pay and bonuses guarantee bad behavior.

Overly centered on revenue

As you rise, revenue becomes more prevalent. Most days, you'd believe revenue was everything. Here’s the problem…

Numbers drain us.

Unless you're a closet math nerd, contemplating and talking about numbers drains your creativity.

Revenue will never substitute impact.

Incapable of taking risks

Corporate success requires taking fewer risks.

Risks can cause dismissal. Risks can interrupt business. Keep things moving so you may keep getting paid your enormous salary and bonus.

Restructuring or layoffs are inevitable. All corporate climbers experience it.

On this fateful day, a small few realize the game they’ve been trapped in and escape. Most return to play for a new company, but it takes time.

Addiction keeps them trapped. You know nothing else. The rest is strange.

You start to think “I’m getting old” or “it’s nearly retirement.” So you settle yet again for the trappings of the corporate ladder game to nowhere.

Should you climb the corporate ladder?

Let me end on a surprising note.

Young people should ascend the corporate ladder. It teaches you business skills and helps support your side gig and (potential) online business.

Don't get trapped, shackled, or muzzled.

Your ideas and creativity become stifled after too much gaming play.

Corporate success won't bring happiness.

Find fulfilling employment that matters. That's it.

Scaling your startup requires answering customer demands, not growth tricks.

I cofounded Freedo Rentals in 2019. I reached 50 lakh+ ARR in 6 months before quitting owing to the epidemic.

Freedo aimed to solve 2 customer pain points:

• Users lacked a reliable last-mile transportation option.

• The amount that Auto walas charge for unmetered services

Solution?

Effectively simple.

Build ports at high-demand spots (colleges, residential societies, metros). Electric ride-sharing can meet demand.

We had many problems scaling. I'll explain using the AARRR model.

• Brand unfamiliarity or a novel product offering were the problems with awareness. Nobody knew what Freedo was or what it did.

• Problem with awareness: Content and advertisements did a poor job of communicating the task at hand. The advertisements clashed with the white-collar part because they were too cheesy.

• Retention Issue: We encountered issues, indicating that the product was insufficient. Problems with keyless entry, creating bills, stealing helmets, etc.

• Retention/Revenue Issue: Costly compared to established rivals. Shared cars were 1/3 of our cost.

• Referral Issue: Missing the opportunity to seize the AHA moment. After the ride, nobody remembered us.

Once you know where you're struggling with AARRR, iterative solutions are usually best.

Once you have nailed the AARRR model, most startups use paid channels to scale. This dependence, on paid channels, increases with scale unless you crack your organic/inbound game.

Over-index growth loops. Growth loops increase inflow and customers as you scale.

When considering growth, ask yourself:

• Who is the solution's ICP (Ideal Customer Profile)? (To whom are you selling)

• What are the most important messages I should convey to customers? (This is an A/B test.)

• Which marketing channels ought I prioritize? (Conduct analysis based on the startup's maturity/stage.)

• Choose the important metrics to monitor for your AARRR funnel (not all metrics are equal)

• Identify the Flywheel effect's growth loops (inertia matters)

My biggest mistakes:

• not paying attention to consumer comments or satisfaction. It is the main cause of problems with referrals, retention, and acquisition for startups. Beyond your NPS, you should consider second-order consequences.

• The tasks at hand should be quite clear.

Here's my scaling equation:

Growth = A x B x C

A = Funnel top (Traffic)

B = Product Valuation (Solving a real pain point)

C = Aha! (Emotional response)

Freedo's A, B, and C created a unique offering.

Freedo’s ABC:

A — Working or Studying population in NCR

B — Electric Vehicles provide last-mile mobility as a clean and affordable solution

C — One click booking with a no-noise scooter

Final outcome:

FWe scaled Freedo to Rs. 50 lakh MRR and were growing 60% month on month till the pandemic ceased our growth story.

How we did it?

We tried ambassadors and coupons. WhatsApp was our most successful A/B test.

We grew widespread adoption through college and society WhatsApp groups. We requested users for referrals in community groups.

What worked for us won't work for others. This scale underwent many revisions.

Every firm is different, thus you must know your customers. Needs to determine which channel to prioritize and when.

Users desired a safe, time-bound means to get there.

This (not mine) growth framework helped me a lot. You should follow suit.

The Merge cut Ethereum's energy use by 99.5%.

The Crypto community celebrated on September 15, 2022. This day, Ethereum Merged. The entire blockchain successfully merged with the Beacon chain, and it was so smooth you barely noticed.

Many have waited, dreaded, and longed for this day.

Some investors feared the network would break down, while others envisioned a seamless merging.

Speculators predict a successful Merge will lead investors to Ethereum. This could boost Ethereum's popularity.

What Has Changed Since The Merge

The merging transitions Ethereum mainnet from PoW to PoS.

PoW sends a mathematical riddle to computers worldwide (miners). First miner to solve puzzle updates blockchain and is rewarded.

The puzzles sent are power-intensive to solve, so mining requires a lot of electricity. It's sent to every miner competing to solve it, requiring duplicate computation.

PoS allows investors to stake their coins to validate a new transaction. Instead of validating a whole block, you validate a transaction and get the fees.

You can validate instead of mine. A validator stakes 32 Ethereum. After staking, the validator can validate future blocks.

Once a validator validates a block, it's sent to a randomly selected group of other validators. This group verifies that a validator is not malicious and doesn't validate fake blocks.

This way, only one computer needs to solve or validate the transaction, instead of all miners. The validated block must be approved by a small group of validators, causing duplicate computation.

PoS is more secure because validating fake blocks results in slashing. You lose your bet tokens. If a validator signs a bad block or double-signs conflicting blocks, their ETH is burned.

Theoretically, Ethereum has one block every 12 seconds, so a validator forging a block risks burning 1 Ethereum for 12 seconds of transactions. This makes mistakes expensive and risky.

What Impact Does This Have On Energy Use?

Cryptocurrency is a natural calamity, sucking electricity and eating away at the earth one transaction at a time.

Many don't know the environmental impact of cryptocurrencies, yet it's tremendous.

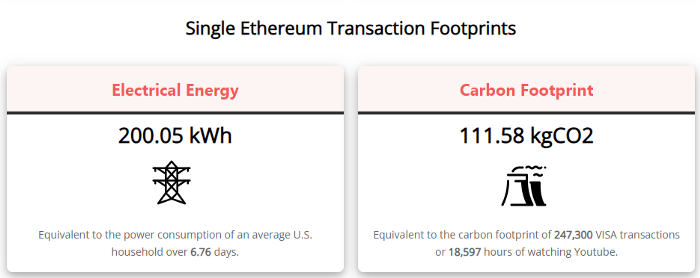
A single Ethereum transaction used to use 200 kWh and leave a large carbon imprint. This update reduces global energy use by 0.2%.

Ethereum will submit a challenge to one validator, and that validator will forward it to randomly selected other validators who accept it.

This reduces the needed computing power.

They expect a 99.5% reduction, therefore a single transaction should cost 1 kWh.

Carbon footprint is 0.58 kgCO2, or 1,235 VISA transactions.

This is a big Ethereum blockchain update.

I love cryptocurrency and Mother Earth.

Sundar Pichai unveiled Simplicity Sprint at Google's latest all-hands conference.

To boost employee efficiency.

Not surprising. Few envisioned Google declaring a productivity drive.

Sunder Pichai's speech:

“There are real concerns that our productivity as a whole is not where it needs to be for the head count we have. Help me create a culture that is more mission-focused, more focused on our products, more customer focused. We should think about how we can minimize distractions and really raise the bar on both product excellence and productivity.”

The primary driver driving Google's efficiency push is:

Google's efficiency push follows 13% quarterly revenue increase. Last year in the same quarter, it was 62%.

Market newcomers may argue that the previous year's figure was fuelled by post-Covid reopening and growing consumer spending. Investors aren't convinced. A promising company like Google can't afford to drop so quickly.

Google’s quarterly revenue growth stood at 13%, against 62% in last year same quarter.

Google isn't alone. In my recent essay regarding 2025 programmers, I warned about the economic downturn's effects on FAAMG's workforce. Facebook had suspended hiring, and Microsoft had promised hefty bonuses for loyal staff.

In the same article, I predicted Google's troubles. Online advertising, especially the way Google and Facebook sell it using user data, is over.

FAAMG and 2nd rung IT companies could be the first to fall without Post-COVID revival and uncertain global geopolitics.

Google has hardly ever discussed effectiveness:

Apparently openly.

Amazon treats its employees like robots, even in software positions. It has significant turnover and a terrible reputation as a result. Because of this, it rarely loses money due to staff productivity.

Amazon trumps Google. In reality, it treats its employees poorly.

Google was the founding father of the modern-day open culture.

Larry and Sergey Google founded the IT industry's Open Culture. Silicon Valley called Google's internal democracy and transparency near anarchy. Management rarely slammed decisions on employees. Surveys and internal polls ensured everyone knew the company's direction and had a vote.

20% project allotment (weekly free time to build own project) was Google's open-secret innovation component.

After Larry and Sergey's exit in 2019, this is Google's first profitability hurdle. Only Google insiders can answer these questions.

• Would Google's investors compel the company's management to adopt an Amazon-style culture where the developers are treated like circus performers?

• If so, would Google follow suit?

• If so, how does Google go about doing it?

Before discussing Google's likely plan, let's examine programming productivity.

What determines a programmer's productivity is simple:

How would we answer Google's questions?

As a programmer, I'm more concerned about Simplicity Sprint's aftermath than its economic catalysts.

Large organizations don't care much about quarterly and annual productivity metrics. They have 10-year product-launch plans. If something seems horrible today, it's likely due to someone's lousy judgment 5 years ago who is no longer in the blame game.

Deconstruct our main question.

• How exactly do you change the culture of the firm so that productivity increases?

• How can you accomplish that without affecting your capacity to profit? There are countless ways to increase output without decreasing profit.

• How can you accomplish this with little to no effect on employee motivation? (While not all employers care about it, in this case we are discussing the father of the open company culture.)

• How do you do it for a 10-developer IT firm that is losing money versus a 1,70,000-developer organization with a trillion-dollar valuation?

When implementing a large-scale organizational change, success must be carefully measured.

The fastest way to do something is to do it right, no matter how long it takes.

You require clearly-defined group/team/role segregation and solid pass/fail matrices to:

• You can give performers rewards.

• Ones that are average can be inspired to improve

• Underachievers may receive assistance or, in the worst-case scenario, rehabilitation

As a 20-year programmer, I associate productivity with greatness.

Doing something well, no matter how long it takes, is the fastest way to do it.

Let's discuss a programmer's productivity.

Why productivity is a strange term in programming:

Productivity is work per unit of time.

Money=time This is an economic proverb. More hours worked, more pay. Longer projects cost more.

As a buyer, you desire a quick supply. As a business owner, you want employees who perform at full capacity, creating more products to transport and boosting your profits.

All economic matrices encourage production because of our obsession with it. Productivity is the only organic way a nation may increase its GDP.

Time is money — is not just a proverb, but an economical fact.

Applying the same productivity theory to programming gets problematic. An automating computer. Its capacity depends on the software its master writes.

Today, a sophisticated program can process a billion records in a few hours. Creating one takes a competent coder and the necessary infrastructure. Learning, designing, coding, testing, and iterations take time.

Programming productivity isn't linear, unlike manufacturing and maintenance.

Average programmers produce code every day yet miss deadlines. Expert programmers go days without coding. End of sprint, they often surprise themselves by delivering fully working solutions.

Reversing the programming duties has no effect. Experts aren't needed for productivity.

These patterns remind me of an XKCD comic.

Programming productivity depends on two factors:

• The capacity of the programmer and his or her command of the principles of computer science

• His or her productive bursts, how often they occur, and how long they last as they engineer the answer

At some point, productivity measurement becomes Schrödinger’s cat.

Product companies measure productivity using use cases, classes, functions, or LOCs (lines of code). In days of data-rich source control systems, programmers' merge requests and/or commits are the most preferred yardstick. Companies assess productivity by tickets closed.

Every organization eventually has trouble measuring productivity. Finer measurements create more chaos. Every measure compares apples to oranges (or worse, apples with aircraft.) On top of the measuring overhead, the endeavor causes tremendous and unnecessary stress on teams, lowering their productivity and defeating its purpose.

Macro productivity measurements make sense. Amazon's factory-era management has done it, but at great cost.

Google can pull it off if it wants to.

What Google meant in reality when it said that employee productivity has decreased:

When Google considers its employees unproductive, it doesn't mean they don't complete enough work in the allotted period.

They can't multiply their work's influence over time.

• Programmers who produce excellent modules or products are unsure on how to use them.

• The best data scientists are unable to add the proper parameters in their models.

• Despite having a great product backlog, managers struggle to recruit resources with the necessary skills.

• Product designers who frequently develop and A/B test newer designs are unaware of why measures are inaccurate or whether they have already reached the saturation point.

• Most ignorant: All of the aforementioned positions are aware of what to do with their deliverables, but neither their supervisors nor Google itself have given them sufficient authority.

So, Google employees aren't productive.

How to fix it?

• Business analysis: White suits introducing novel items can interact with customers from all regions. Track analytics events proactively, especially the infrequent ones.

• SOLID, DRY, TEST, and AUTOMATION: Do less + reuse. Use boilerplate code creation. If something already exists, don't implement it yourself.

• Build features-building capabilities: N features are created by average programmers in N hours. An endless number of features can be built by average programmers thanks to the fact that expert programmers can produce 1 capability in N hours.

• Work on projects that will have a positive impact: Use the same algorithm to search for images on YouTube rather than the Mars surface.

• Avoid tasks that can only be measured in terms of time linearity at all costs (if a task can be completed in N minutes, then M copies of the same task would cost M*N minutes).

In conclusion:

Software development isn't linear. Why should the makers be measured?

Notation for The Big O

I'm discussing a new way to quantify programmer productivity. (It applies to other professions, but that's another subject)

The Big O notation expresses the paradigm (the algorithmic performance concept programmers rot to ace their Google interview)

Google (or any large corporation) can do this.

1. Sort organizational roles into categories and specify their impact vs. time objectives. A CXO role's time vs. effect function, for instance, has a complexity of O(log N), meaning that if a CEO raises his or her work time by 8x, the result only increases by 3x.

2. Plot the influence of each employee over time using the X and Y axes, respectively.

3. Add a multiplier for Y-axis values to the productivity equation to make business objectives matter. (Example values: Support = 5, Utility = 7, and Innovation = 10).

4. Compare employee scores in comparable categories (developers vs. devs, CXOs vs. CXOs, etc.) and reward or help employees based on whether they are ahead of or behind the pack.

After measuring every employee's inventiveness, it's straightforward to help underachievers and praise achievers.

Example of a Big(O) Category:

If I ran Google (God forbid, its worst days are far off), here's how I'd classify it. You can categorize Google employees whichever you choose.

The Google interview truth:

O(1) < O(log n) < O(n) < O(n log n) < O(n^x) where all logarithmic bases are < n.

O(1): Customer service workers' hours have no impact on firm profitability or customer pleasure.

CXOs Most of their time is spent on travel, strategic meetings, parties, and/or meetings with minimal floor-level influence. They're good at launching new products but bad at pivoting without disaster. Their directions are being followed.

Devops, UX designers, testers Agile projects revolve around deployment. DevOps controls the levers. Their automation secures results in subsequent cycles.

UX/UI Designers must still prototype UI elements despite improved design tools.

All test cases are proportional to use cases/functional units, hence testers' work is O(N).

Architects Their effort improves code quality. Their right/wrong interference affects product quality and rollout decisions even after the design is set.

Core Developers Only core developers can write code and own requirements. When people understand and own their labor, the output improves dramatically. A single character error can spread undetected throughout the SDLC and cost millions.

Core devs introduce/eliminate 1000x bugs, refactoring attempts, and regression. Following our earlier hypothesis.

The fastest way to do something is to do it right, no matter how long it takes.

Conclusion:

Google is at the liberal extreme of the employee-handling spectrum

Microsoft faced an existential crisis after 2000. It didn't choose Amazon's data-driven people management to revitalize itself.

Instead, it entrusted developers. It welcomed emerging technologies and opened up to open source, something it previously opposed.

Google is too lax in its employee-handling practices. With that foundation, it can only follow Amazon, no matter how carefully.

Any attempt to redefine people's measurements will affect the organization emotionally.

The more Google compares apples to apples, the higher its chances for future rebirth.