Framework to Evaluate Metaverse and Web3
Everywhere we turn, there's a new metaverse or Web3 debut. Microsoft recently announced a $68.7 BILLION cash purchase of Activision.
Like AI in 2013 and blockchain in 2014, NFT growth in 2021 feels like this year's metaverse and Web3 growth. We are all bombarded with information, conflicting signals, and a sensation of FOMO.
How can we evaluate the metaverse and Web3 in a noisy, new world? My framework for evaluating upcoming technologies and themes is shown below. I hope you will also find them helpful.
Understand the “pipes” in a new space.
Whatever people say, Metaverse and Web3 will have to coexist with the current Internet. Companies who host, move, and store data over the Internet have a lot of intriguing use cases in Metaverse and Web3, whether in infrastructure, data analytics, or compliance. Hence the following point.
## Understand the apps layer and their infrastructure.
Gaming, crypto exchanges, and NFT marketplaces would not exist today if not for technology that enables rapid app creation. Yes, according to Chainalysis and other research, 30–40% of Ethereum is self-hosted, with the rest hosted by large cloud providers. For Microsoft to acquire Activision makes strategic sense. It's not only about the games, but also the infrastructure that supports them.
Follow the money
Understanding how money and wealth flow in a complex and dynamic environment helps build clarity. Unless you are exceedingly wealthy, you have limited ability to significantly engage in the Web3 economy today. Few can just buy 10 ETH and spend it in one day. You must comprehend who benefits from the process, and how that 10 ETH circulates now and possibly tomorrow. Major holders and players control supply and liquidity in any market. Today, most Web3 apps are designed to increase capital inflow so existing significant holders can utilize it to create a nascent Web3 economy. When you see a new Metaverse or Web3 application, remember how money flows.
What is the use case?
What does the app do? If there is no clear use case with clear makers and consumers solving a real problem, then the euphoria soon fades, and the only stakeholders who remain enthused are those who have too much to lose.
Time is a major competition that is often overlooked.
We're only busier, but each day is still 24 hours. Using new apps may mean that time is lost doing other things. The user must be eager to learn. Metaverse and Web3 vs. our time? I don't think we know the answer yet (at least for working adults whose cost of time is higher).
I don't think we know the answer yet (at least for working adults whose cost of time is higher).
People and organizations need security and transparency.
For new technologies or apps to be widely used, they must be safe, transparent, and trustworthy. What does secure Metaverse and Web3 mean? This is an intriguing subject for both the business and public sectors. Cloud adoption grew in part due to improved security and data protection regulations.
The following frameworks can help analyze and understand new technologies and emerging technological topics, unless you are a significant investment fund with the financial ability to gamble on numerous initiatives and essentially form your own “index fund”.
I write on VC, startups, and leadership.
More on https://www.linkedin.com/in/joycejshen/ and https://joyceshen.substack.com/
This writing is my own opinion and does not represent investment advice.
More on Web3 & Crypto

Percy Bolmér
3 years ago
Ethereum No Longer Consumes A Medium-Sized Country's Electricity To Run
The Merge cut Ethereum's energy use by 99.5%.

The Crypto community celebrated on September 15, 2022. This day, Ethereum Merged. The entire blockchain successfully merged with the Beacon chain, and it was so smooth you barely noticed.
Many have waited, dreaded, and longed for this day.
Some investors feared the network would break down, while others envisioned a seamless merging.
Speculators predict a successful Merge will lead investors to Ethereum. This could boost Ethereum's popularity.
What Has Changed Since The Merge
The merging transitions Ethereum mainnet from PoW to PoS.
PoW sends a mathematical riddle to computers worldwide (miners). First miner to solve puzzle updates blockchain and is rewarded.
The puzzles sent are power-intensive to solve, so mining requires a lot of electricity. It's sent to every miner competing to solve it, requiring duplicate computation.
PoS allows investors to stake their coins to validate a new transaction. Instead of validating a whole block, you validate a transaction and get the fees.
You can validate instead of mine. A validator stakes 32 Ethereum. After staking, the validator can validate future blocks.
Once a validator validates a block, it's sent to a randomly selected group of other validators. This group verifies that a validator is not malicious and doesn't validate fake blocks.
This way, only one computer needs to solve or validate the transaction, instead of all miners. The validated block must be approved by a small group of validators, causing duplicate computation.
PoS is more secure because validating fake blocks results in slashing. You lose your bet tokens. If a validator signs a bad block or double-signs conflicting blocks, their ETH is burned.
Theoretically, Ethereum has one block every 12 seconds, so a validator forging a block risks burning 1 Ethereum for 12 seconds of transactions. This makes mistakes expensive and risky.
What Impact Does This Have On Energy Use?
Cryptocurrency is a natural calamity, sucking electricity and eating away at the earth one transaction at a time.
Many don't know the environmental impact of cryptocurrencies, yet it's tremendous.
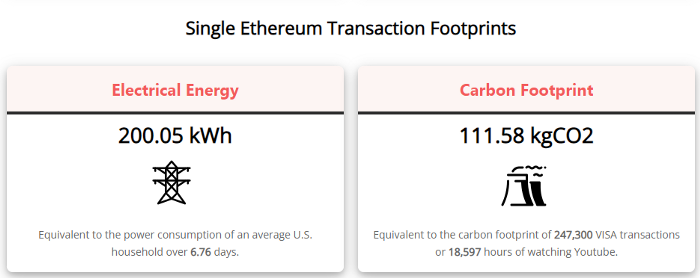
A single Ethereum transaction used to use 200 kWh and leave a large carbon imprint. This update reduces global energy use by 0.2%.
Ethereum will submit a challenge to one validator, and that validator will forward it to randomly selected other validators who accept it.
This reduces the needed computing power.
They expect a 99.5% reduction, therefore a single transaction should cost 1 kWh.
Carbon footprint is 0.58 kgCO2, or 1,235 VISA transactions.
This is a big Ethereum blockchain update.
I love cryptocurrency and Mother Earth.
Sam Hickmann
4 years ago
A quick guide to formatting your text on INTΞGRITY
[06/20/2022 update] We have now implemented a powerful text editor, but you can still use markdown.
Markdown:
Headers
SYNTAX:
# This is a heading 1
## This is a heading 2
### This is a heading 3
#### This is a heading 4
RESULT:
This is a heading 1
This is a heading 2
This is a heading 3
This is a heading 4
Emphasis
SYNTAX:
**This text will be bold**
~~Strikethrough~~
*You **can** combine them*
RESULT:
This text will be italic
This text will be bold
You can combine them
Images
SYNTAX:

RESULT:
Videos
SYNTAX:
https://www.youtube.com/watch?v=7KXGZAEWzn0
RESULT:
Links
SYNTAX:
[Int3grity website](https://www.int3grity.com)
RESULT:
Tweets
SYNTAX:
https://twitter.com/samhickmann/status/1503800505864130561
RESULT:
Blockquotes
SYNTAX:
> Human beings face ever more complex and urgent problems, and their effectiveness in dealing with these problems is a matter that is critical to the stability and continued progress of society. \- Doug Engelbart, 1961
RESULT:
Human beings face ever more complex and urgent problems, and their effectiveness in dealing with these problems is a matter that is critical to the stability and continued progress of society. - Doug Engelbart, 1961
Inline code
SYNTAX:
Text inside `backticks` on a line will be formatted like code.
RESULT:
Text inside backticks on a line will be formatted like code.
Code blocks
SYNTAX:
'''js
function fancyAlert(arg) {
if(arg) {
$.facebox({div:'#foo'})
}
}
'''
RESULT:
function fancyAlert(arg) {
if(arg) {
$.facebox({div:'#foo'})
}
}
Maths
We support LaTex to typeset math. We recommend reading the full documentation on the official website
SYNTAX:
$$[x^n+y^n=z^n]$$
RESULT:
[x^n+y^n=z^n]
Tables
SYNTAX:
| header a | header b |
| ---- | ---- |
| row 1 col 1 | row 1 col 2 |
RESULT:
| header a | header b | header c |
|---|---|---|
| row 1 col 1 | row 1 col 2 | row 1 col 3 |

ANDREW SINGER
3 years ago
Crypto seen as the ‘future of money’ in inflation-mired countries
Crypto as the ‘future of money' in inflation-stricken nations
Citizens of devalued currencies “need” crypto. “Nice to have” in the developed world.
According to Gemini's 2022 Global State of Crypto report, cryptocurrencies “evolved from what many considered a niche investment into an established asset class” last year.
More than half of crypto owners in Brazil (51%), Hong Kong (51%), and India (54%), according to the report, bought cryptocurrency for the first time in 2021.
The study found that inflation and currency devaluation are powerful drivers of crypto adoption, especially in emerging market (EM) countries:
“Respondents in countries that have seen a 50% or greater devaluation of their currency against the USD over the last decade were more than 5 times as likely to plan to purchase crypto in the coming year.”
Between 2011 and 2021, the real lost 218 percent of its value against the dollar, and 45 percent of Brazilians surveyed by Gemini said they planned to buy crypto in 2019.
The rand (South Africa's currency) has fallen 103 percent in value over the last decade, second only to the Brazilian real, and 32 percent of South Africans expect to own crypto in the coming year. Mexico and India, the third and fourth highest devaluation countries, followed suit.
Compared to the US dollar, Hong Kong and the UK currencies have not devalued in the last decade. Meanwhile, only 5% and 8% of those surveyed in those countries expressed interest in buying crypto.
What can be concluded? Noah Perlman, COO of Gemini, sees various crypto use cases depending on one's location.
‘Need to have' investment in countries where the local currency has devalued against the dollar, whereas in the developed world it is still seen as a ‘nice to have'.
Crypto as money substitute
As an adjunct professor at New York University School of Law, Winston Ma distinguishes between an asset used as an inflation hedge and one used as a currency replacement.
Unlike gold, he believes Bitcoin (BTC) is not a “inflation hedge”. They acted more like growth stocks in 2022. “Bitcoin correlated more closely with the S&P 500 index — and Ether with the NASDAQ — than gold,” he told Cointelegraph. But in the developing world, things are different:
“Inflation may be a primary driver of cryptocurrency adoption in emerging markets like Brazil, India, and Mexico.”
According to Justin d'Anethan, institutional sales director at the Amber Group, a Singapore-based digital asset firm, early adoption was driven by countries where currency stability and/or access to proper banking services were issues. Simply put, he said, developing countries want alternatives to easily debased fiat currencies.
“The larger flows may still come from institutions and developed countries, but the actual users may come from places like Lebanon, Turkey, Venezuela, and Indonesia.”
“Inflation is one of the factors that has and continues to drive adoption of Bitcoin and other crypto assets globally,” said Sean Stein Smith, assistant professor of economics and business at Lehman College.
But it's only one factor, and different regions have different factors, says Stein Smith. As a “instantaneously accessible, traceable, and cost-effective transaction option,” investors and entrepreneurs increasingly recognize the benefits of crypto assets. Other places promote crypto adoption due to “potential capital gains and returns”.
According to the report, “legal uncertainty around cryptocurrency,” tax questions, and a general education deficit could hinder adoption in Asia Pacific and Latin America. In Africa, 56% of respondents said more educational resources were needed to explain cryptocurrencies.
Not only inflation, but empowering our youth to live better than their parents without fear of failure or allegiance to legacy financial markets or products, said Monica Singer, ConsenSys South Africa lead. Also, “the issue of cash and remittances is huge in Africa, as is the issue of social grants.”
Money's future?
The survey found that Brazil and Indonesia had the most cryptocurrency ownership. In each country, 41% of those polled said they owned crypto. Only 20% of Americans surveyed said they owned cryptocurrency.
These markets are more likely to see cryptocurrencies as the future of money. The survey found:
“The majority of respondents in Latin America (59%) and Africa (58%) say crypto is the future of money.”
Brazil (66%), Nigeria (63%), Indonesia (61%), and South Africa (57%). Europe and Australia had the fewest believers, with Denmark at 12%, Norway at 15%, and Australia at 17%.
Will the Ukraine conflict impact adoption?
The poll was taken before the war. Will the devastating conflict slow global crypto adoption growth?
With over $100 million in crypto donations directly requested by the Ukrainian government since the war began, Stein Smith says the war has certainly brought crypto into the mainstream conversation.
“This real-world demonstration of decentralized money's power could spur wider adoption, policy debate, and increased use of crypto as a medium of exchange.”
But the war may not affect all developing nations. “The Ukraine war has no impact on African demand for crypto,” Others loom larger. “Yes, inflation, but also a lack of trust in government in many African countries, and a young demographic very familiar with mobile phones and the internet.”
A major success story like Mpesa in Kenya has influenced the continent and may help accelerate crypto adoption. Creating a plan when everyone you trust fails you is directly related to the African spirit, she said.
On the other hand, Ma views the Ukraine conflict as a sort of crisis check for cryptocurrencies. For those in emerging markets, the Ukraine-Russia war has served as a “stress test” for the cryptocurrency payment rail, he told Cointelegraph.
“These emerging markets may see the greatest future gains in crypto adoption.”
Inflation and currency devaluation are persistent global concerns. In such places, Bitcoin and other cryptocurrencies are now seen as the “future of money.” Not in the developed world, but that could change with better regulation and education. Inflation and its impact on cash holdings are waking up even Western nations.
Read original post here.
You might also like

Bradley Vangelder
3 years ago
How we started and then quickly sold our startup
From a simple landing where we tested our MVP to a platform that distributes 20,000 codes per month, we learned a lot.

Starting point
Kwotet was my first startup. Everyone might post book quotes online.
I wanted a change.
Kwotet lacked attention, thus I felt stuck. After experiencing the trials of starting Kwotet, I thought of developing a waitlist service, but I required a strong co-founder.
I knew Dries from school, but we weren't close. He was an entrepreneurial programmer who worked a lot outside school. I needed this.
We brainstormed throughout school hours. We developed features to put us first. We worked until 3 am to launch this product.
Putting in the hours is KEY when building a startup

The instant that we lost our spark
In Belgium, college seniors do their internship in their last semester.
As we both made the decision to pick a quite challenging company, little time was left for Lancero.
Eventually, we lost interest. We lost the spark…
The only logical choice was to find someone with the same spark we started with to acquire Lancero.
And we did @ MicroAcquire.
Sell before your product dies. Make sure to profit from all the gains.
What did we do following the sale?
Not far from selling Lancero I lost my dad. I was about to start a new company. It was focused on positivity. I got none left at the time.
We still didn’t let go of the dream of becoming full-time entrepreneurs. As Dries launched the amazing company Plunk, and I’m still in the discovering stages of my next journey!

Dream!
You’re an entrepreneur if:
You're imaginative.
You enjoy disassembling and reassembling things.
You're adept at making new friends.
YOU HAVE DREAMS.
You don’t need to believe me if I tell you “everything is possible”… I wouldn't believe it myself if anyone told me this 2 years ago.
Until I started doing, living my dreams.

Nick
3 years ago
This Is How Much Quora Paid Me For 23 Million Content Views
You’ll be surprised; I sure was

Blogging and writing online as a side income has now been around for a significant amount of time. Nowadays, it is a continuously rising moneymaker for prospective writers, with several writing platforms existing online. At the top of the list are Medium, Vocal Media, Newsbreak, and the biggest one of them, Quora, with 300 million active users.
Quora, unlike Medium, is a question-and-answer format platform. On Medium you are permitted to write what you want, while on Quora, you answer questions on topics that you have expertise about. Quora, like Medium, now compensates its authors for the answers they provide in comparison to the previous, in which you had to be admitted to the partner program and were paid to ask questions.
Quora just recently went live with this new partner program, Quora Plus, and the way it works is that it is a subscription for $5 a month which provides you access to metered/monetized stories, in turn compensating the writers for part of that subscription for their answers.
I too on Quora have found a lot of success on the platform, gaining 23 Million Content Views, and 300,000 followers for my space, which is kind of the Quora equivalent of a Medium article. The way in which I was able to do this was entirely thanks to a hack that I uncovered to the Quora algorithm.
In this article, I plan on discussing how much money I received from 23 million content views on Quora, and I bet you’ll be shocked; I know I was.
A Brief Explanation of How I Got 23 Million Views and How You Can Do It Too
On Quora, everything in terms of obtaining views is about finding the proper question, which I only understood quite late into the game. I published my first response in 2019 but never actually wrote on Quora until the summer of 2020, and about a month into posting consistently I found out how to find the perfect question. Here’s how:
The Process
Go to your Home Page and start scrolling… While browsing, check for the following things…
Answers from people you follow or your followers.
Advertisements
These two things are the two things you want to ignore, you don’t want to answer those questions or look at the ads. You should now be left with a couple of recommended answers. To discover which recommended answer is the best to answer as well, look at these three important aspects.
Date of the answer: Was it in the past few days, preferably 2–3 days, even better, past 24 hours?
Views: Are they in the ten thousands or hundred thousands?
Upvotes: Are they in the hundreds or thousands?
Now, choose an answer to a question which you think you could answer as well that satisfies the requirements above. Once you click on it, as all answers on Quora works, it will redirect you to the page for that question, in which you will have to select once again if you should answer the question.
Amount of answers: How many responses are there to the given question? This tells you how much competition you have. My rule is beyond 25 answers, you shouldn’t answer, but you can change it anyway you’d like.
Answerers: Who did the answering for the question? If the question includes a bunch of renowned, extremely well-known people on Quora, there’s a good possibility your essay is going to get drowned out.
Views: Check for a constant quantity of high views on each answer for the question; this is what will guarantee that your answer gets a lot of views!
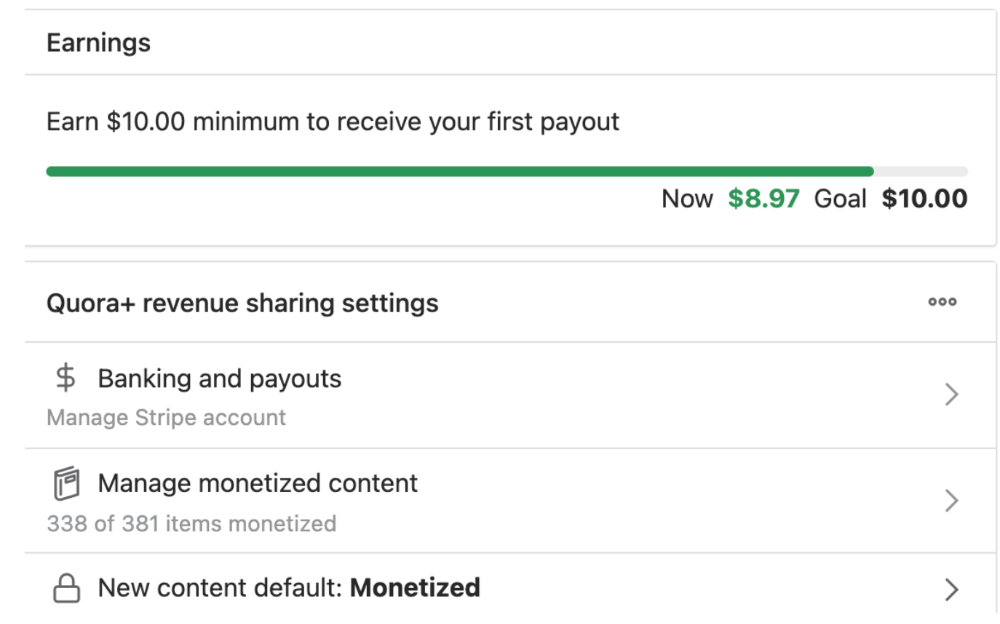
The Income Reveal! How Much I Made From 23 Million Content Views
DRUM ROLL, PLEASE!
8.97 USD. Yes, not even ten dollars, not even nine. Just eight dollars and ninety-seven cents.
Possible Reasons for My Low Earnings
Quora Plus and the answering partner program are newer than my Quora views.
Few people use Quora+, therefore revenues are low.
I haven't been writing much on Quora, so I'm only making money from old answers and a handful since Quora Plus launched.
Quora + pays poorly...
Should You Try Quora and Quora For Money?
My answer depends on your needs. I never got invited to Quora's question partner program due to my late start, but other writers have made hundreds. Due to Quora's new and competitive answering partner program, you may not make much money.
If you want a fun writing community, try Quora. Quora was fun when I only made money from my space. Quora +'s paywalls and new contributors eager to make money have made the platform less fun for me.
This article is a summary to save you time. You can read my full, more detailed article, here.

Chris Newman
3 years ago
Clean Food: Get Over Yourself If You Want to Save the World.

I’m a permaculture farmer. I want to create food-producing ecosystems. My hope is a world with easy access to a cuisine that nourishes consumers, supports producers, and leaves the Earth joyously habitable.
Permaculturists, natural farmers, plantsmen, and foodies share this ambition. I believe this group of green thumbs, stock-folk, and food champions is falling to tribalism, forgetting that rescuing the globe requires saving all of its inhabitants, even those who adore cheap burgers and Coke. We're digging foxholes and turning folks who disagree with us or don't understand into monsters.
Take Dr. Daphne Miller's comments at the end of her Slow Money Journal interview:
“Americans are going to fall into two camps when all is said and done: People who buy cheap goods, regardless of quality, versus people who are willing and able to pay for things that are made with integrity. We are seeing the limits of the “buying cheap crap” approach.”
This is one of the most judgmental things I've read outside the Bible. Consequences:
People who purchase inexpensive things (food) are ignorant buffoons who prefer to choose fair trade coffee over fuel as long as the price is correct.
It all depends on your WILL to buy quality or cheaply. Both those who are WILLING and those who ARE NOT exist. And able, too.
People who are unwilling and unable are purchasing garbage. You're giving your kids bad food. Both the Earth and you are being destroyed by your actions. Your camp is the wrong one. You’re garbage! Disgrace to you.
Dr. Miller didn't say it, but words are worthless until interpreted. This interpretation depends on the interpreter's economic, racial, political, religious, family, and personal history. Complementary language insults another. Imagine how that Brown/Harvard M.D.'s comment sounds to a low-income household with no savings.

Dr. Miller's comment reflects the echo chamber into which nearly all clean food advocates speak. It asks easy questions and accepts non-solutions like raising food prices and eating less meat. People like me have cultivated an insular world unencumbered by challenges beyond the margins. We may disagree about technical details in rotationally-grazing livestock, but we short circuit when asked how our system could supply half the global beef demand. Most people have never seriously considered this question. We're so loved and affirmed that challenging ourselves doesn't seem necessary. Were generals insisting we don't need to study the terrain because God is on our side?
“Yes, the $8/lb ground beef is produced the way it should be. Yes, it’s good for my body. Yes it’s good for the Earth. But it’s eight freaking dollars, and my kid needs braces and protein. Bye Felicia, we’re going to McDonald’s.”
-Bobby Q. Homemaker
Funny clean foodies. People don't pay enough for food; they should value it more. Turn the concept of buying food with integrity into a wedge and drive it into the heart of America, dividing the willing and unwilling.
We go apeshit if you call our products high-end.
I've heard all sorts of gaslighting to defend a $10/lb pork chop as accessible (things I’ve definitely said in the past):
At Whole Foods, it costs more.
The steak at the supermarket is overly affordable.
Pay me immediately or the doctor gets paid later.
I spoke with Timbercreek Market and Local Food Hub in front of 60 people. We were asked about local food availability.
They came to me last, after my co-panelists gave the same responses I would have given two years before.
I grumbled, "Our food is inaccessible." Nope. It's beyond the wallets of nearly everyone, and it's the biggest problem with sustainable food systems. We're criminally unserious about being leaders in sustainability until we propose solutions beyond economic relativism, wishful thinking, and insisting that vulnerable, distracted people do all the heavy lifting of finding a way to afford our food. And until we talk about solutions, all this preserve the world? False.
The room fell silent as if I'd revealed a terrible secret. Long, thunderous applause followed my other remarks. But I’m probably not getting invited back to any VNRLI events.
I make pricey cuisine. It’s high-end. I have customers who really have to stretch to get it, and they let me know it. They're forgoing other creature comforts to help me make a living and keep the Earth of my grandmothers alive, and they're doing it as an act of love. They believe in us and our work.
I remember it when I'm up to my shoulders in frigid water, when my vehicle stinks of four types of shit, when I come home covered in blood and mud, when I'm hauling water in 100-degree heat, when I'm herding pigs in a rainstorm and dodging lightning bolts to close the chickens. I'm reminded I'm not alone. Their enthusiasm is worth more than money; it helps me make a life and a living. I won't label that gift less than it is to make my meal seem more accessible.
Not everyone can sacrifice.
Let's not pretend we want to go back to peasant fare, despite our nostalgia. Industrial food has leveled what rich and poor eat. How food is cooked will be the largest difference between what you and a billionaire eat. Rich and poor have access to chicken, pork, and beef. You might be shocked how recently that wasn't the case. This abundance, particularly of animal protein, has helped vulnerable individuals.

Industrial food causes environmental damage, chronic disease, and distribution inequities. Clean food promotes non-industrial, artisan farming. This creates a higher-quality, more expensive product than the competition; we respond with aggressive marketing and the "people need to value food more" shtick geared at consumers who can spend the extra money.
The guy who is NOT able is rendered invisible by clean food's elitist marketing, which is bizarre given a.) clean food insists it's trying to save the world, yet b.) MOST PEOPLE IN THE WORLD ARE THAT GUY. No one can help him except feel-good charities. That's crazy.
Also wrong: a foodie telling a kid he can't eat a 99-cent fast food hamburger because it lacks integrity. Telling him how easy it is to save his ducketts and maybe have a grass-fed house burger at the end of the month as a reward, but in the meantime get your protein from canned beans you can't bake because you don't have a stove and, even if you did, your mom works two jobs and moonlights as an Uber driver so she doesn't have time to heat that shitup anyway.
A wealthy person's attitude toward the poor is indecent. It's 18th-century Versailles.

Human rights include access to nutritious food without social or environmental costs. As a food-forest-loving permaculture farmer, I no longer balk at the concept of cultured beef and hydroponics. My food is out of reach for many people, but access to decent food shouldn't be. Cultures and hydroponics could scale to meet the clean food affordability gap without externalities. If technology can deliver great, affordable beef without environmental negative effects, I can't reject it because it's new, unusual, or might endanger my business.
Why is your farm needed if cultured beef and hydroponics can feed the world? Permaculture food forests with trees, perennial plants, and animals are crucial to economically successful environmental protection. No matter how advanced technology gets, we still need clean air, water, soil, greenspace, and food.
Clean Food cultivated in/on live soil, minimally processed, and eaten close to harvest is part of the answer, not THE solution. Clean food advocates must recognize the conflicts at the intersection of environmental, social, and economic sustainability, the disproportionate effects of those conflicts on the poor and lower-middle classes, and the immorality and impracticality of insisting vulnerable people address those conflicts on their own and judging them if they don't.
Our clients, relatives, friends, and communities need an honest assessment of our role in a sustainable future. If we're serious about preserving the world, we owe honesty to non-customers. We owe our goal and sanity to honesty. Future health and happiness of the world left to the average person's pocketbook and long-term moral considerations is a dismal proposition with few parallels.
Let's make soil and grow food. Let the lab folks do their thing. We're all interdependent.
