More on Economics & Investing

Theresa W. Carey
3 years ago
How Payment for Order Flow (PFOF) Works
What is PFOF?
PFOF is a brokerage firm's compensation for directing orders to different parties for trade execution. The brokerage firm receives fractions of a penny per share for directing the order to a market maker.
Each optionable stock could have thousands of contracts, so market makers dominate options trades. Order flow payments average less than $0.50 per option contract.
Order Flow Payments (PFOF) Explained
The proliferation of exchanges and electronic communication networks has complicated equity and options trading (ECNs) Ironically, Bernard Madoff, the Ponzi schemer, pioneered pay-for-order-flow.
In a December 2000 study on PFOF, the SEC said, "Payment for order flow is a method of transferring trading profits from market making to brokers who route customer orders to specialists for execution."
Given the complexity of trading thousands of stocks on multiple exchanges, market making has grown. Market makers are large firms that specialize in a set of stocks and options, maintaining an inventory of shares and contracts for buyers and sellers. Market makers are paid the bid-ask spread. Spreads have narrowed since 2001, when exchanges switched to decimals. A market maker's ability to play both sides of trades is key to profitability.
Benefits, requirements
A broker receives fees from a third party for order flow, sometimes without a client's knowledge. This invites conflicts of interest and criticism. Regulation NMS from 2005 requires brokers to disclose their policies and financial relationships with market makers.
Your broker must tell you if it's paid to send your orders to specific parties. This must be done at account opening and annually. The firm must disclose whether it participates in payment-for-order-flow and, upon request, every paid order. Brokerage clients can request payment data on specific transactions, but the response takes weeks.
Order flow payments save money. Smaller brokerage firms can benefit from routing orders through market makers and getting paid. This allows brokerage firms to send their orders to another firm to be executed with other orders, reducing costs. The market maker or exchange benefits from additional share volume, so it pays brokerage firms to direct traffic.
Retail investors, who lack bargaining power, may benefit from order-filling competition. Arrangements to steer the business in one direction invite wrongdoing, which can erode investor confidence in financial markets and their players.
Pay-for-order-flow criticism
It has always been controversial. Several firms offering zero-commission trades in the late 1990s routed orders to untrustworthy market makers. During the end of fractional pricing, the smallest stock spread was $0.125. Options spreads widened. Traders found that some of their "free" trades cost them a lot because they weren't getting the best price.
The SEC then studied the issue, focusing on options trades, and nearly decided to ban PFOF. The proliferation of options exchanges narrowed spreads because there was more competition for executing orders. Options market makers said their services provided liquidity. In its conclusion, the report said, "While increased multiple-listing produced immediate economic benefits to investors in the form of narrower quotes and effective spreads, these improvements have been muted with the spread of payment for order flow and internalization."
The SEC allowed payment for order flow to continue to prevent exchanges from gaining monopoly power. What would happen to trades if the practice was outlawed was also unclear. SEC requires brokers to disclose financial arrangements with market makers. Since then, the SEC has watched closely.
2020 Order Flow Payment
Rule 605 and Rule 606 show execution quality and order flow payment statistics on a broker's website. Despite being required by the SEC, these reports can be hard to find. The SEC mandated these reports in 2005, but the format and reporting requirements have changed over the years, most recently in 2018.
Brokers and market makers formed a working group with the Financial Information Forum (FIF) to standardize order execution quality reporting. Only one retail brokerage (Fidelity) and one market maker remain (Two Sigma Securities). FIF notes that the 605/606 reports "do not provide the level of information that allows a retail investor to gauge how well a broker-dealer fills a retail order compared to the NBBO (national best bid or offer’) at the time the order was received by the executing broker-dealer."
In the first quarter of 2020, Rule 606 reporting changed to require brokers to report net payments from market makers for S&P 500 and non-S&P 500 equity trades and options trades. Brokers must disclose payment rates per 100 shares by order type (market orders, marketable limit orders, non-marketable limit orders, and other orders).
Richard Repetto, Managing Director of New York-based Piper Sandler & Co., publishes a report on Rule 606 broker reports. Repetto focused on Charles Schwab, TD Ameritrade, E-TRADE, and Robinhood in Q2 2020. Repetto reported that payment for order flow was higher in the second quarter than the first due to increased trading activity, and that options paid more than equities.
Repetto says PFOF contributions rose overall. Schwab has the lowest options rates, while TD Ameritrade and Robinhood have the highest. Robinhood had the highest equity rating. Repetto assumes Robinhood's ability to charge higher PFOF reflects their order flow profitability and that they receive a fixed rate per spread (vs. a fixed rate per share by the other brokers).
Robinhood's PFOF in equities and options grew the most quarter-over-quarter of the four brokers Piper Sandler analyzed, as did their implied volumes. All four brokers saw higher PFOF rates.
TD Ameritrade took the biggest income hit when cutting trading commissions in fall 2019, and this report shows they're trying to make up the shortfall by routing orders for additional PFOF. Robinhood refuses to disclose trading statistics using the same metrics as the rest of the industry, offering only a vague explanation on their website.
Summary
Payment for order flow has become a major source of revenue as brokers offer no-commission equity (stock and ETF) orders. For retail investors, payment for order flow poses a problem because the brokerage may route orders to a market maker for its own benefit, not the investor's.
Infrequent or small-volume traders may not notice their broker's PFOF practices. Frequent traders and those who trade larger quantities should learn about their broker's order routing system to ensure they're not losing out on price improvement due to a broker prioritizing payment for order flow.
This post is a summary. Read full article here

Sofien Kaabar, CFA
3 years ago
How to Make a Trading Heatmap
Python Heatmap Technical Indicator

Heatmaps provide an instant overview. They can be used with correlations or to predict reactions or confirm the trend in trading. This article covers RSI heatmap creation.
The Market System
Market regime:
Bullish trend: The market tends to make higher highs, which indicates that the overall trend is upward.
Sideways: The market tends to fluctuate while staying within predetermined zones.
Bearish trend: The market has the propensity to make lower lows, indicating that the overall trend is downward.
Most tools detect the trend, but we cannot predict the next state. The best way to solve this problem is to assume the current state will continue and trade any reactions, preferably in the trend.
If the EURUSD is above its moving average and making higher highs, a trend-following strategy would be to wait for dips before buying and assuming the bullish trend will continue.
Indicator of Relative Strength
J. Welles Wilder Jr. introduced the RSI, a popular and versatile technical indicator. Used as a contrarian indicator to exploit extreme reactions. Calculating the default RSI usually involves these steps:
Determine the difference between the closing prices from the prior ones.
Distinguish between the positive and negative net changes.
Create a smoothed moving average for both the absolute values of the positive net changes and the negative net changes.
Take the difference between the smoothed positive and negative changes. The Relative Strength RS will be the name we use to describe this calculation.
To obtain the RSI, use the normalization formula shown below for each time step.
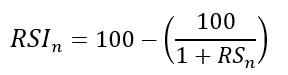
The 13-period RSI and black GBPUSD hourly values are shown above. RSI bounces near 25 and pauses around 75. Python requires a four-column OHLC array for RSI coding.
import numpy as np
def add_column(data, times):
for i in range(1, times + 1):
new = np.zeros((len(data), 1), dtype = float)
data = np.append(data, new, axis = 1)
return data
def delete_column(data, index, times):
for i in range(1, times + 1):
data = np.delete(data, index, axis = 1)
return data
def delete_row(data, number):
data = data[number:, ]
return data
def ma(data, lookback, close, position):
data = add_column(data, 1)
for i in range(len(data)):
try:
data[i, position] = (data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
data = delete_row(data, lookback)
return data
def smoothed_ma(data, alpha, lookback, close, position):
lookback = (2 * lookback) - 1
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
data = ma(data, lookback, close, position)
data[lookback + 1, position] = (data[lookback + 1, close] * alpha) + (data[lookback, position] * beta)
for i in range(lookback + 2, len(data)):
try:
data[i, position] = (data[i, close] * alpha) + (data[i - 1, position] * beta)
except IndexError:
pass
return data
def rsi(data, lookback, close, position):
data = add_column(data, 5)
for i in range(len(data)):
data[i, position] = data[i, close] - data[i - 1, close]
for i in range(len(data)):
if data[i, position] > 0:
data[i, position + 1] = data[i, position]
elif data[i, position] < 0:
data[i, position + 2] = abs(data[i, position])
data = smoothed_ma(data, 2, lookback, position + 1, position + 3)
data = smoothed_ma(data, 2, lookback, position + 2, position + 4)
data[:, position + 5] = data[:, position + 3] / data[:, position + 4]
data[:, position + 6] = (100 - (100 / (1 + data[:, position + 5])))
data = delete_column(data, position, 6)
data = delete_row(data, lookback)
return dataMake sure to focus on the concepts and not the code. You can find the codes of most of my strategies in my books. The most important thing is to comprehend the techniques and strategies.
My weekly market sentiment report uses complex and simple models to understand the current positioning and predict the future direction of several major markets. Check out the report here:
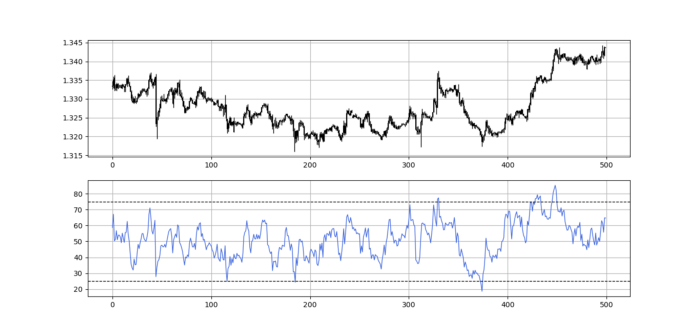
Using the Heatmap to Find the Trend
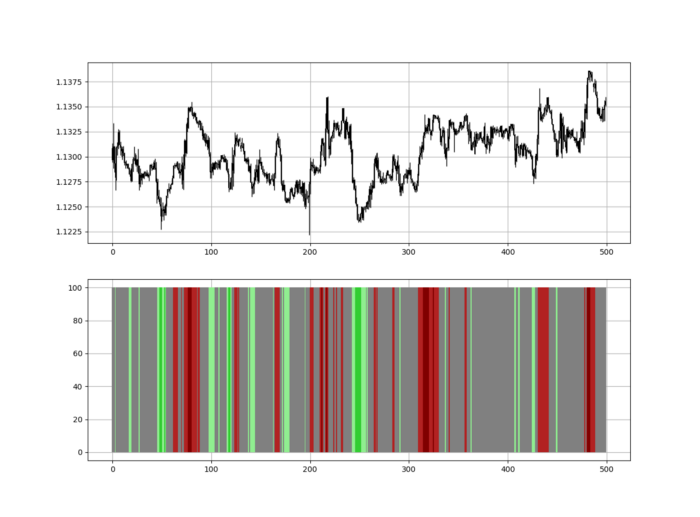
RSI trend detection is easy but useless. Bullish and bearish regimes are in effect when the RSI is above or below 50, respectively. Tracing a vertical colored line creates the conditions below. How:
When the RSI is higher than 50, a green vertical line is drawn.
When the RSI is lower than 50, a red vertical line is drawn.
Zooming out yields a basic heatmap, as shown below.
Plot code:
def indicator_plot(data, second_panel, window = 250):
fig, ax = plt.subplots(2, figsize = (10, 5))
sample = data[-window:, ]
for i in range(len(sample)):
ax[0].vlines(x = i, ymin = sample[i, 2], ymax = sample[i, 1], color = 'black', linewidth = 1)
if sample[i, 3] > sample[i, 0]:
ax[0].vlines(x = i, ymin = sample[i, 0], ymax = sample[i, 3], color = 'black', linewidth = 1.5)
if sample[i, 3] < sample[i, 0]:
ax[0].vlines(x = i, ymin = sample[i, 3], ymax = sample[i, 0], color = 'black', linewidth = 1.5)
if sample[i, 3] == sample[i, 0]:
ax[0].vlines(x = i, ymin = sample[i, 3], ymax = sample[i, 0], color = 'black', linewidth = 1.5)
ax[0].grid()
for i in range(len(sample)):
if sample[i, second_panel] > 50:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'green', linewidth = 1.5)
if sample[i, second_panel] < 50:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'red', linewidth = 1.5)
ax[1].grid()
indicator_plot(my_data, 4, window = 500)
Call RSI on your OHLC array's fifth column. 4. Adjusting lookback parameters reduces lag and false signals. Other indicators and conditions are possible.
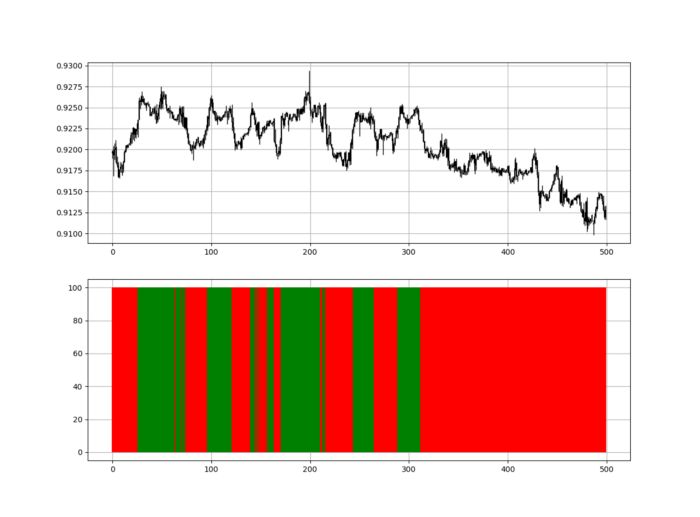
Another suggestion is to develop an RSI Heatmap for Extreme Conditions.
Contrarian indicator RSI. The following rules apply:
Whenever the RSI is approaching the upper values, the color approaches red.
The color tends toward green whenever the RSI is getting close to the lower values.
Zooming out yields a basic heatmap, as shown below.
Plot code:
import matplotlib.pyplot as plt
def indicator_plot(data, second_panel, window = 250):
fig, ax = plt.subplots(2, figsize = (10, 5))
sample = data[-window:, ]
for i in range(len(sample)):
ax[0].vlines(x = i, ymin = sample[i, 2], ymax = sample[i, 1], color = 'black', linewidth = 1)
if sample[i, 3] > sample[i, 0]:
ax[0].vlines(x = i, ymin = sample[i, 0], ymax = sample[i, 3], color = 'black', linewidth = 1.5)
if sample[i, 3] < sample[i, 0]:
ax[0].vlines(x = i, ymin = sample[i, 3], ymax = sample[i, 0], color = 'black', linewidth = 1.5)
if sample[i, 3] == sample[i, 0]:
ax[0].vlines(x = i, ymin = sample[i, 3], ymax = sample[i, 0], color = 'black', linewidth = 1.5)
ax[0].grid()
for i in range(len(sample)):
if sample[i, second_panel] > 90:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'red', linewidth = 1.5)
if sample[i, second_panel] > 80 and sample[i, second_panel] < 90:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'darkred', linewidth = 1.5)
if sample[i, second_panel] > 70 and sample[i, second_panel] < 80:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'maroon', linewidth = 1.5)
if sample[i, second_panel] > 60 and sample[i, second_panel] < 70:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'firebrick', linewidth = 1.5)
if sample[i, second_panel] > 50 and sample[i, second_panel] < 60:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'grey', linewidth = 1.5)
if sample[i, second_panel] > 40 and sample[i, second_panel] < 50:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'grey', linewidth = 1.5)
if sample[i, second_panel] > 30 and sample[i, second_panel] < 40:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'lightgreen', linewidth = 1.5)
if sample[i, second_panel] > 20 and sample[i, second_panel] < 30:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'limegreen', linewidth = 1.5)
if sample[i, second_panel] > 10 and sample[i, second_panel] < 20:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'seagreen', linewidth = 1.5)
if sample[i, second_panel] > 0 and sample[i, second_panel] < 10:
ax[1].vlines(x = i, ymin = 0, ymax = 100, color = 'green', linewidth = 1.5)
ax[1].grid()
indicator_plot(my_data, 4, window = 500)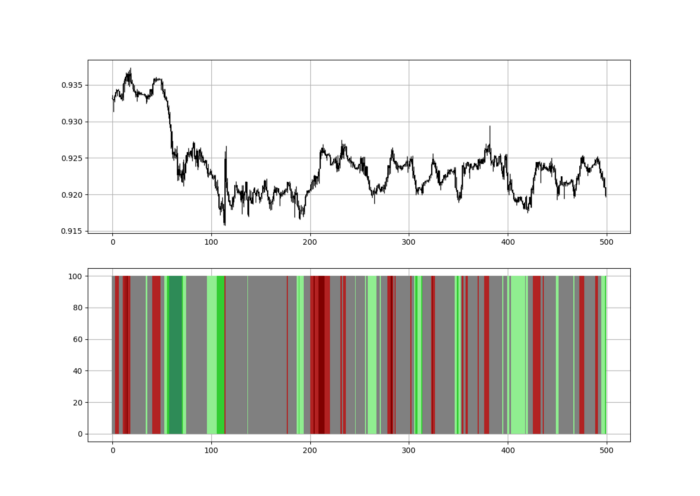
Dark green and red areas indicate imminent bullish and bearish reactions, respectively. RSI around 50 is grey.
Summary
To conclude, my goal is to contribute to objective technical analysis, which promotes more transparent methods and strategies that must be back-tested before implementation.
Technical analysis will lose its reputation as subjective and unscientific.
When you find a trading strategy or technique, follow these steps:
Put emotions aside and adopt a critical mindset.
Test it in the past under conditions and simulations taken from real life.
Try optimizing it and performing a forward test if you find any potential.
Transaction costs and any slippage simulation should always be included in your tests.
Risk management and position sizing should always be considered in your tests.
After checking the above, monitor the strategy because market dynamics may change and make it unprofitable.

Jan-Patrick Barnert
3 years ago
Wall Street's Bear Market May Stick Around
If history is any guide, this bear market might be long and severe.
This is the S&P 500 Index's fourth such incident in 20 years. The last bear market of 2020 was a "shock trade" caused by the Covid-19 pandemic, although earlier ones in 2000 and 2008 took longer to bottom out and recover.
Peter Garnry, head of equities strategy at Saxo Bank A/S, compares the current selloff to the dotcom bust of 2000 and the 1973-1974 bear market marked by soaring oil prices connected to an OPEC oil embargo. He blamed high tech valuations and the commodity crises.
"This drop might stretch over a year and reach 35%," Garnry wrote.
Here are six bear market charts.
Time/depth
The S&P 500 Index plummeted 51% between 2000 and 2002 and 58% during the global financial crisis; it took more than 1,000 trading days to recover. The former took 638 days to reach a bottom, while the latter took 352 days, suggesting the present selloff is young.
Valuations
Before the tech bubble burst in 2000, valuations were high. The S&P 500's forward P/E was 25 times then. Before the market fell this year, ahead values were near 24. Before the global financial crisis, stocks were relatively inexpensive, but valuations dropped more than 40%, compared to less than 30% now.
Earnings
Every stock crash, especially earlier bear markets, returned stocks to fundamentals. The S&P 500 decouples from earnings trends but eventually recouples.
Support
Central banks won't support equity investors just now. The end of massive monetary easing will terminate a two-year bull run that was among the strongest ever, and equities may struggle without cheap money. After years of "don't fight the Fed," investors must embrace a new strategy.
Bear Haunting Bear
If the past is any indication, rising government bond yields are bad news. After the financial crisis, skyrocketing rates and a falling euro pushed European stock markets back into bear territory in 2011.
Inflation/rates
The current monetary policy climate differs from past bear markets. This is the first time in a while that markets face significant inflation and rising rates.
This post is a summary. Read full article here
You might also like

The woman
3 years ago
Why Google's Hiring Process is Brilliant for Top Tech Talent
Without a degree and experience, you can get a high-paying tech job.

Most organizations follow this hiring rule: you chat with HR, interview with your future boss and other senior managers, and they make the final hiring choice.
If you've ever applied for a job, you know how arduous it can be. A newly snapped photo and a glossy resume template can wear you out. Applying to Google can change this experience.
According to an Universum report, Google is one of the world's most coveted employers. It's not simply the search giant's name and reputation that attract candidates, but its role requirements or lack thereof.
Candidates no longer need a beautiful resume, cover letter, Ivy League laurels, or years of direct experience. The company requires no degree or experience.
Elon Musk started it. He employed the two-hands test to uncover talented non-graduates. The billionaire eliminated the requirement for experience.
Google is deconstructing traditional employment with programs like the Google Project Management Degree, a free online and self-paced professional credential course.
Google's hiring is interesting. After its certification course, applicants can work in project management. Instead of academic degrees and experience, the company analyzes coursework.
Google finds the best project managers and technical staff in exchange. Google uses three strategies to find top talent.
Chase down the innovators
Google eliminates restrictions like education, experience, and others to find the polar bear amid the snowfall. Google's free project management education makes project manager responsibilities accessible to everyone.
Many jobs don't require a degree. Overlooking individuals without a degree can make it difficult to locate a candidate who can provide value to a firm.
Firsthand knowledge follows the same rule. A lack of past information might be an employer's benefit. This is true for creative teams or businesses that prefer to innovate.
Or when corporations conduct differently from the competition. No-experience candidates can offer fresh perspectives. Fast Company reports that people with no sales experience beat those with 10 to 15 years of experience.
Give the aptitude test first priority.
Google wants the best candidates. Google wouldn't be able to receive more applications if it couldn't screen them for fit. Its well-organized online training program can be utilized as a portfolio.
Google learns a lot about an applicant through completed assignments. It reveals their ability, leadership style, communication capability, etc. The course mimics the job to assess candidates' suitability.
Basic screening questions might provide information to compare candidates. Any size small business can use screening questions and test projects to evaluate prospective employees.
Effective training for employees
Businesses must train employees regardless of their hiring purpose. Formal education and prior experience don't guarantee success. Maintaining your employees' professional knowledge gaps is key to their productivity and happiness. Top-notch training can do that. Learning and development are key to employee engagement, says Bob Nelson, author of 1,001 Ways to Engage Employees.
Google's online certification program isn't available everywhere. Improving the recruiting process means emphasizing aptitude over experience and a degree. Instead of employing new personnel and having them work the way their former firm trained them, train them how you want them to function.
If you want to know more about Google’s recruiting process, we recommend you watch the movie “Internship.”

Tora Northman
3 years ago
Pixelmon NFTs are so bad, they are almost good!
Bored Apes prices continue to rise, HAPEBEAST launches, Invisible Friends hype continues to grow. Sadly, not all projects are as successful.
Of course, there are many factors to consider when buying an NFT. Is the project a scam? Will the reveal derail the project? Possibly, but when Pixelmon first teased its launch, it generated a lot of buzz.
With a primary sale mint price of 3 ETH ($8,100 USD), it started as an expensive project, with plenty of fans willing to invest in what was sold as a game. After it was revealed, it fell rapidly.
Why? It was overpromised and under delivered.
According to the project's creator[^1], the funds generated will be used to develop the artwork. "The Pixelmon reveal was wrong. This is what our Pixelmon look like in-game. "Despite the fud, I will not go anywhere," he wrote on Twitter. The goal remains. The funds will still be used to build our game. I will finish this project."
The project raised $70 million USD, but the NFTs buyers received were not the project's original teasers. Some call it "the worst NFT project ever," while others call it a complete scam.
But there's hope for some buyers. Kevin emerged from the ashes as the project was roasted over the fire.
A Minecraft character meets Salad Fingers - that's Kevin. He's a frog-like creature whose reveal was such a terrible NFT that it became part of history – and a meme.
If you're laughing at people paying $8K for a silly pixelated image, you might need to take it back. Precisely because of this, lucky holders who minted Kevin have been able to sell the now-memed NFT for over 8 ETH (around $24,000 USD), with some currently listed for 100 ETH.
Of course, Twitter has been awash in memes mocking those who invested in the project, because what else can you do when so many people lose money?
It's still unclear if the NFT project is a scam, but the team behind it was hired on Upwork. There's still hope for redemption, but Kevin's rise to fame appears to be the only positive outcome so far.
[^1] This is not the first time the creator (A 20-yo New Zealanders) has sought money via an online platform and had people claiming he under-delivered. He raised $74,000 on Kickstarter for a card game called Psycho Chicken. There are hundreds of comments on the Kickstarter project saying they haven't received the product and pleading for a refund or an update.

Jerry Keszka
3 years ago
10 Crazy Useful Free Websites No One Told You About But You Needed
The internet is a massive information resource. With so much stuff, it's easy to forget about useful websites. Here are five essential websites you may not have known about.

1. Companies.tools
Companies.tools are what successful startups employ. This website offers a curated selection of design, research, coding, support, and feedback resources. Ct has the latest app development platform and greatest client feedback method.
2. Excel Formula Bot
Excel Formula Bot can help if you forget a formula. Formula Bot uses AI to convert text instructions into Excel formulas, so you don't have to remember them.
Just tell the Bot what to do, and it will do it. Excel Formula Bot can calculate sales tax and vacation days. When you're stuck, let the Bot help.
3.TypeLit
TypeLit helps you improve your typing abilities while reading great literature.
TypeLit.io lets you type any book or dozens of preset classics. TypeLit provides real-time feedback on accuracy and speed.
Goals and progress can be tracked. Why not improve your typing and learn great literature with TypeLit?
4. Calm Schedule
Finding a meeting time that works for everyone is difficult. Personal and business calendars might be difficult to coordinate.
Synchronize your two calendars to save time and avoid problems. You may avoid searching through many calendars for conflicts and keep your personal information secret. Having one source of truth for personal and work occasions will help you never miss another appointment.
https://calmcalendar.com/
5. myNoise
myNoise makes the outside world quieter. myNoise is the right noise for a noisy office or busy street.
If you can't locate the right noise, make it. MyNoise unlocks the world. Shut out distractions. Thank your ears.
6. Synthesia
Professional videos require directors, filmmakers, editors, and animators. Now, thanks to AI, you can generate high-quality videos without video editing experience.
AI avatars are crucial. You can design a personalized avatar using a web-based software like synthesia.io. Our avatars can lip-sync in over 60 languages, so you can make worldwide videos. There's an AI avatar for every video goal.
Not free. Amazing service, though.
7. Cleaning-up-images
Have you shot a wonderful photo just to notice something in the background? You may have a beautiful headshot but wish to erase an imperfection.
Cleanup.pictures removes undesirable objects from photos. Our algorithms will eliminate the selected object.
Cleanup.pictures can help you obtain the ideal shot every time. Next time you take images, let Cleanup.pictures fix any flaws.
8. PDF24 Tools
Editing a PDF can be a pain. Most of us don't know Adobe Acrobat's functionalities. Why buy something you'll rarely use? Better options exist.
PDF24 is an online PDF editor that's free and subscription-free. Rotate, merge, split, compress, and convert PDFs in your browser. PDF24 makes document signing easy.
Upload your document, sign it (or generate a digital signature), and download it. It's easy and free. PDF24 is a free alternative to pricey PDF editing software.
9. Class Central
Finding online classes is much easier. Class Central has classes from Harvard, Stanford, Coursera, Udemy, and Google, Amazon, etc. in one spot.
Whether you want to acquire a new skill or increase your knowledge, you'll find something. New courses bring variety.
10. Rome2rio
Foreign travel offers countless transport alternatives. How do you get from A to B? It’s easy!
Rome2rio will show you the best method to get there, including which mode of transport is ideal.
Plane
Car
Train
Bus
Ferry
Driving
Shared bikes
Walking
Do you know any free, useful websites?